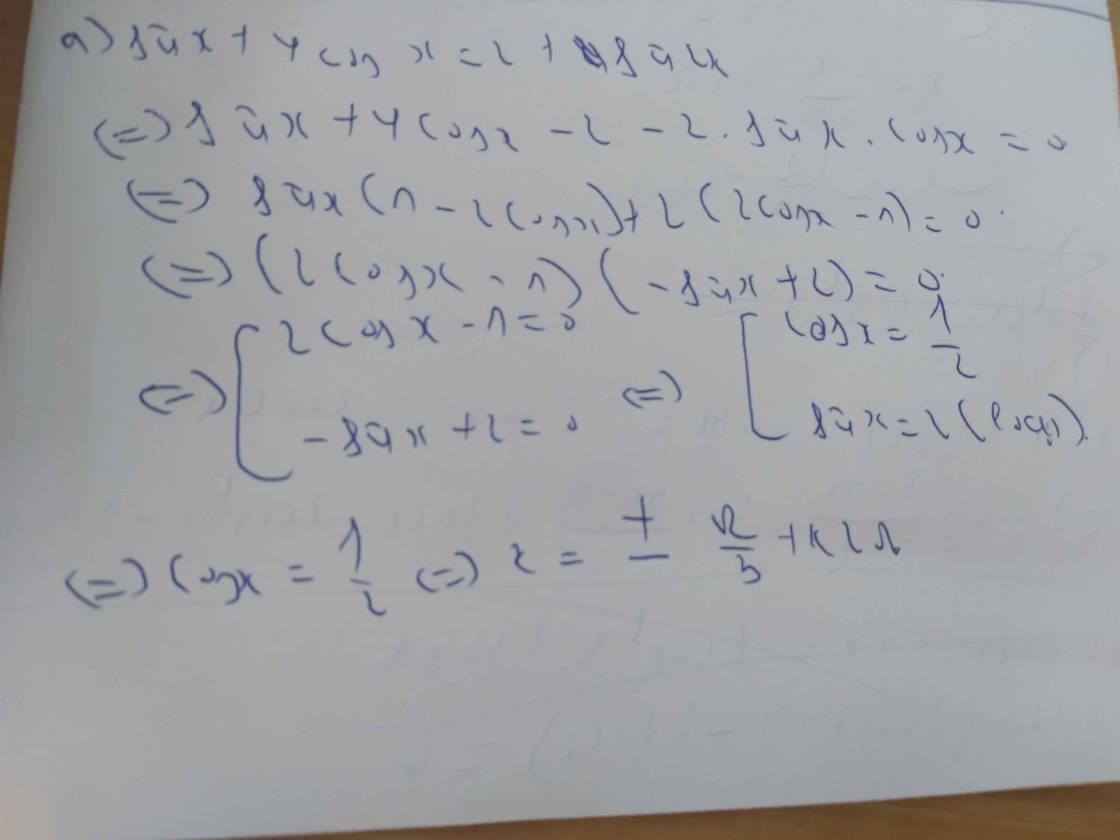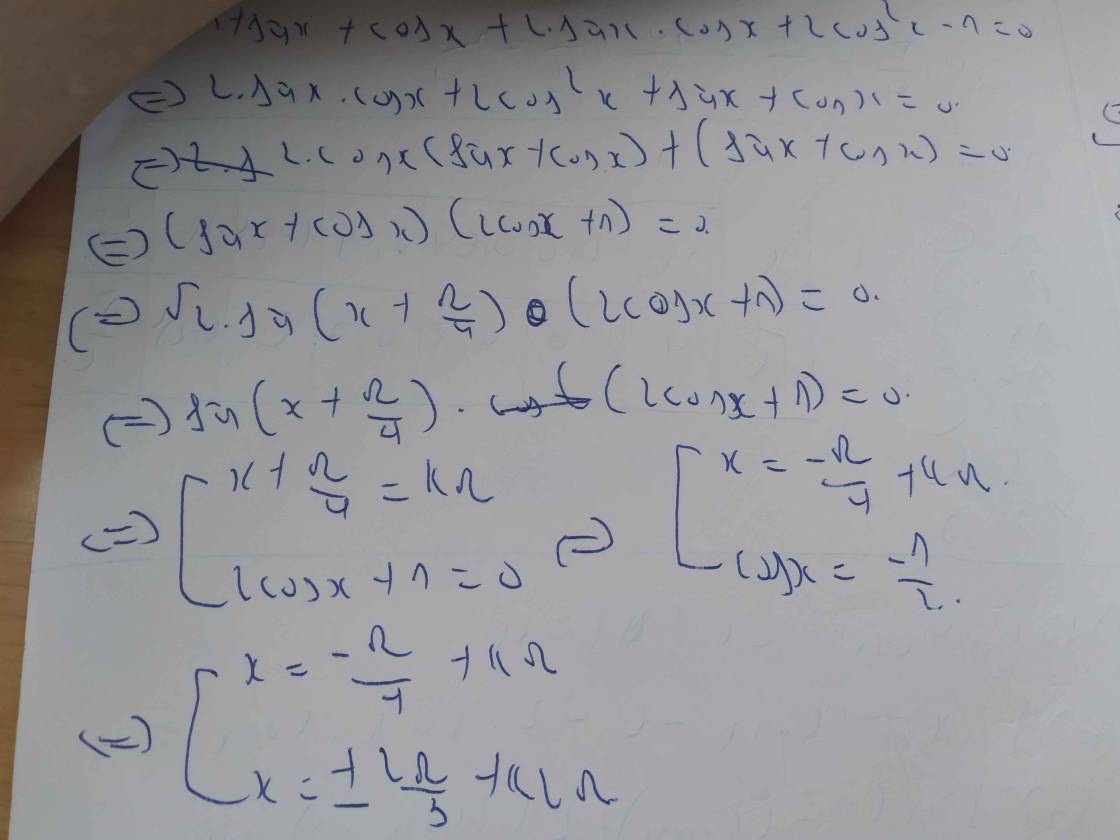b: \(\Leftrightarrow2\cdot\cos2x\cdot\cos x+2\cdot\sin x\cdot\cos2x=\sqrt{2}\cdot\cos2x\)

\(\Leftrightarrow2\cdot\cos2x\left(\sin x+\cos x\right)=\sqrt{2}\cdot\cos2x\)

\(\Leftrightarrow\sqrt{2}\cdot\cos2x\cdot\left[\sqrt{2}\cdot\sqrt{2}\cdot\sin\left(x+\dfrac{\Pi}{4}\right)-1\right]=0\)

\(\Leftrightarrow\left[{}\begin{matrix}\cos2x=0\\\sin\left(x+\dfrac{\Pi}{4}\right)=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\Pi}{2}+k\Pi\\x+\dfrac{\Pi}{4}=\dfrac{\Pi}{6}+k2\Pi\\x+\dfrac{\Pi}{4}=\dfrac{5}{6}\Pi+k2\Pi\end{matrix}\right.\)

\(\Leftrightarrow x\in\left\{\dfrac{\Pi}{4}+\dfrac{k\Pi}{2};\dfrac{-1}{12}\Pi+k2\Pi;\dfrac{7}{12}\Pi+k2\Pi\right\}\)

c: \(\Leftrightarrow2\cdot\sin2x\cdot\cos x+\sin2x=2\cdot\cos2x\cdot\cos x+\cos2x\)

\(\Leftrightarrow\sin2x\left(2\cos x+1\right)=\cos2x\left(2\cos x+1\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}\sin2x=\cos2x=\sin\left(\dfrac{\Pi}{2}-2x\right)\\\cos x=-\dfrac{1}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\Pi}{8}+\dfrac{k\Pi}{4}\\\\x=-\dfrac{2}{3}\Pi+k2\Pi\\x=\dfrac{2}{3}\Pi+k2\Pi\end{matrix}\right.\)

\(\sqrt{2}sinx+sin2x=\sqrt{3}cos2x-\sqrt{6}cosx\)

\(\Leftrightarrow\dfrac{\sqrt{2}}{2}sinx+\dfrac{1}{2}sin2x-\dfrac{\sqrt{3}}{2}cos2x+\dfrac{\sqrt{6}}{2}cosx=0\)

\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{3}\right)+sin\left(2x-\dfrac{\pi}{3}\right)=0\)

\(\Leftrightarrow\sqrt{2}cos\left(x-\dfrac{\pi}{6}\right)+2sin\left(x-\dfrac{\pi}{6}\right).cos\left(x-\dfrac{\pi}{6}\right)=0\)

\(\Leftrightarrow\sqrt{2}cos\left(x-\dfrac{\pi}{6}\right)\left[1+\sqrt{2}sin\left(x-\dfrac{\pi}{6}\right)\right]=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cos\left(x-\dfrac{\pi}{6}\right)=0\\sin\left(x-\dfrac{\pi}{6}\right)=-\dfrac{1}{\sqrt{2}}\end{matrix}\right.\)

Đến đấy thì dễ rồi.

\(\Leftrightarrow\sqrt{2}\left(\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx\right)+\dfrac{1}{2}sin2x-\dfrac{\sqrt{3}}{2}cos2x=0\)

\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{3}\right)+sin\left(2x-\dfrac{\pi}{3}\right)=0\)

Đặt \(x+\dfrac{\pi}{3}=u\Rightarrow2x-\dfrac{\pi}{3}=2u-\pi\)

\(\Rightarrow\sqrt{2}sinu+sin\left(2u-\pi\right)=0\)

\(\Leftrightarrow\sqrt{2}sinu-sin2u=0\)

\(\Leftrightarrow sinu\left(\sqrt{2}-2cosu\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sinu=0\\cosu=\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x+\dfrac{\pi}{3}\right)=0\\cos\left(x+\dfrac{\pi}{3}\right)=\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)

\(\Leftrightarrow...\)

hộ vs ae ơi

`cos 2x+\sqrt{3}sin 2x+\sqrt{3}sin x-cos x=4`

`<=>1/2 cos 2x+\sqrt{3}/2 sin 2x+\sqrt{3}/2 sin x-1/2 cos x=2`

`<=>sin(\pi/6 +2x)+sin(x-\pi/6)=2`

Vì `-1 <= sin (\pi/6 +2x) <= 1`

     `-1 <= sin (x-\pi/6) <= 1`

 Dấu "`=`" xảy ra `<=>{(sin(\pi/6+2x)=1),(sin(x-\pi/6)=1):}`

        `<=>{(\pi/6+2x=\pi/2+k2\pi),(x-\pi/6=\pi/2+k2\pi):}`

        `<=>{(x=\pi/6+k\pi),(x=[2\pi]/3+k2\pi):}`    `(k in ZZ)`

1.

\(2sin\left(x+\dfrac{\pi}{6}\right)+sinx+2cosx=3\)

\(\Leftrightarrow\sqrt{3}sinx+cosx+sinx+2cosx=3\)

\(\Leftrightarrow\left(\sqrt{3}+1\right)sinx+3cosx=3\)

\(\Leftrightarrow\sqrt{13+2\sqrt{3}}\left[\dfrac{\sqrt{3}+1}{\sqrt{13+2\sqrt{3}}}sinx+\dfrac{3}{\sqrt{13+2\sqrt{3}}}cosx\right]=3\)

Đặt \(\alpha=arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}\)

\(pt\Leftrightarrow\sqrt{13+2\sqrt{3}}sin\left(x+\alpha\right)=3\)

\(\Leftrightarrow sin\left(x+\alpha\right)=\dfrac{3}{\sqrt{13+2\sqrt{3}}}\)

\(\Leftrightarrow\left[{}\begin{matrix}x+\alpha=arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\\x+\alpha=\pi-arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pi-2arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\end{matrix}\right.\)

Vậy phương trình đã cho có nghiệm:

\(x=k2\pi;x=\pi-2arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\)

2.

\(\left(sin2x+cos2x\right)cosx+2cos2x-sinx=0\)

\(\Leftrightarrow2sinx.cos^2x+cos2x.cosx+2cos2x-sinx=0\)

\(\Leftrightarrow\left(2cos^2x-1\right)sinx+cos2x.cosx+2cos2x=0\)

\(\Leftrightarrow cos2x.sinx+cos2x.cosx+2cos2x=0\)

\(\Leftrightarrow cos2x.\left(sinx+cosx+2\right)=0\)

\(\Leftrightarrow cos2x=0\)

\(\Leftrightarrow2x=\dfrac{\pi}{2}+k\pi\)

\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)

Vậy phương trình đã cho có nghiệm \(x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)