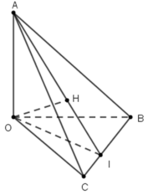
Cho tứ diện OABC có OA,OB,OC đôi một vuông góc với nhau. Kẻ OH vuông góc với mặt phẳng (ABC) tại H. Khẳng định nào sau đây là sai
A. 1 O H 2 = 1 O A 2 + 1 O B 2 + 1 O C 2
B.H là trực tâm tam giác ABC
C. O A ⊥ B C
D. A H ⊥ O B C
Những câu hỏi liên quan
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Kẻ OH vuông góc với mặt phẳng (ABC) tại H. Khẳng định nào sau đây là sai? A.
1
O
H
2
1
O
A
2
+
1
O
B
2
+...
Đọc tiếp
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Kẻ OH vuông góc với mặt phẳng (ABC) tại H. Khẳng định nào sau đây là sai?
A. 1 O H 2 = 1 O A 2 + 1 O B 2 + 1 O C 2
B. H là trực tâm tam giác ABC
C. O A ⊥ B C
D. A H ⊥ O B C
Cho tứ diện OABC có OA,OB,OC đôi một vuông góc với nhau. Kẻ OH vuông góc với mặt phẳng (ABC) tại H. Khẳng định nào sau đây là sai? A.
A
H
⊥
(
O
B
C
)
B.
O
A
⊥
B
C
C. H là trực tâm tam giác ABC D....
Đọc tiếp
Cho tứ diện OABC có OA,OB,OC đôi một vuông góc với nhau. Kẻ OH vuông góc với mặt phẳng (ABC) tại H. Khẳng định nào sau đây là sai?
A. A H ⊥ ( O B C )
B. O A ⊥ B C
C. H là trực tâm tam giác ABC
D. 1 O H 2 = 1 O A 2 + 1 O B 2 + 1 O C 2
Đáp án A
*) Vì OA,OB,OC đôi một vuông góc với nhau nên
*)
theo trên B C ⊥ O A ⇒ B C ⊥ A H (2).
Từ (1) và (2) H là trực tâm tam giác ABC
*) Kẻ O I ⊥ B C tại I; O H ⊥ A I tại H
⇒ O H ⊥ ( A B C )
Ta có trong tam giác vuông OAC vuông tại O và OBC vuông tại O:
Đúng 0
Bình luận (0)
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Kẻ OH vuông góc với mặt phẳng (ABC) tại H. Khẳng định nào sau đây là sai?
Đọc tiếp
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Kẻ OH vuông góc với mặt phẳng (ABC) tại H. Khẳng định nào sau đây là sai?
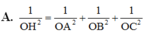
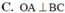
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Kẻ OH vuông góc với mặt phẳng (ABC) tại H. Khẳng định nào sau đây là sai? A.
1
O
H
2
1
O
A
2...
Đọc tiếp
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Kẻ OH vuông góc với mặt phẳng (ABC) tại H. Khẳng định nào sau đây là sai?
A. 1 O H 2 = 1 O A 2 + 1 O B 2 + 1 O C 2
B. H là trực tâm tam giác ABC
C. OA ⊥ BC
D. AH ⊥ (OBC)
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Gọi H là hình chiếu của O trên mặt phẳng (ABC). Mệnh đề nào sau đây đúng A. H là trung điểm của AC B. H là trọng tâm tam giác ABC C. H là trung điểm của BC D. H là trực tâm của tam giác ABC
Đọc tiếp
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Gọi H là hình chiếu của O trên mặt phẳng (ABC). Mệnh đề nào sau đây đúng
A. H là trung điểm của AC
B. H là trọng tâm tam giác ABC
C. H là trung điểm của BC
D. H là trực tâm của tam giác ABC
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau, OA
a
2
2
, OBOCa. Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC). Tính thể tích khối tứ diện OABH. A.
a
3
2
6
B.
a
3...
Đọc tiếp
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau, OA = a 2 2 , OB=OC=a. Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC). Tính thể tích khối tứ diện OABH.
A. a 3 2 6
B. a 3 2 12
C. a 3 2 24
D. a 3 2 48
Chọn D
Từ giả thiết suy ra: ΔABC cân tại A có:
Gọi I là trung điểm của BC ⇒ A I ⊥ B C
Giả sử H là trực tâm của tam giác ABC.
Ta thấy O A ⊥ O B C
Vì O B ⊥ O A C ⇒ O B ⊥ A C và A C ⊥ B H nên A C ⊥ O B H ⇒ O H ⊥ A C ( 1 )
B C ⊥ O A I ⇒ O H ⊥ B C ( 2 )
Từ (1) và (2) suy ra O H ⊥ A B C
Có O I = 1 2 B C = a 2 2 = O A
=> ΔAOI vuông cân tại O => H là trung điểm AI và O H = 1 2 A I = a 2
Khi đó:
Đúng 0
Bình luận (0)
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau, OA
a
2
2
, OB OC a. Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC) Tính thể tích khối tứ diện OABH A.
a
3
2
6
B.
a...
Đọc tiếp
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau, OA = a 2 2 , OB= OC =a. Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC) Tính thể tích khối tứ diện OABH
A. a 3 2 6
B. a 3 2 12
C. a 3 2 24
D. a 3 2 48
Cho tứ diện OABC có ba cạnh OA;OB;OC đôi một vuông góc với nhau,
O
A
a
2
2
,
O
B
O
C
a
. Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC)Tính thể tích khối tứ diện OABH A.
a
3
2
6...
Đọc tiếp
Cho tứ diện OABC có ba cạnh OA;OB;OC đôi một vuông góc với nhau, O A = a 2 2 , O B = O C = a . Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC)Tính thể tích khối tứ diện OABH
A. a 3 2 6
B. a 3 2 12
C. a 3 2 24
D. a 3 2 48
Đáp án D
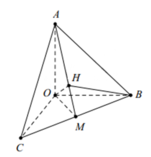
Gọi M là trung điểm của B C ⇒ B M ⊥ O A M
Vì O H ⊥ A B C ⇒ 1 O H 2 = 1 O A 2 + 1 O B 2 + 1 O C 2 ⇒ O H = a 2
Tam giác OAH vuông tại H, có A H = O A 2 − O H 2 = a 2
Diện tích tam giác vuông OAH là S Δ O A H = 1 2 . O H . A H = a 2 8
Thể tích khối chóp OABH là
V O A B H = 1 3 . B M . S Δ O A H = 1 3 . a 2 2 . a 2 8 = a 3 2 48
Đúng 0
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
16 tháng 8 2023 lúc 18:32
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và \(OA = a,OB = a\sqrt 2 \) và \(OC = 2a\). Tính khoảng cách từ điểm \(O\) đến mặt phẳng \((ABC)\).
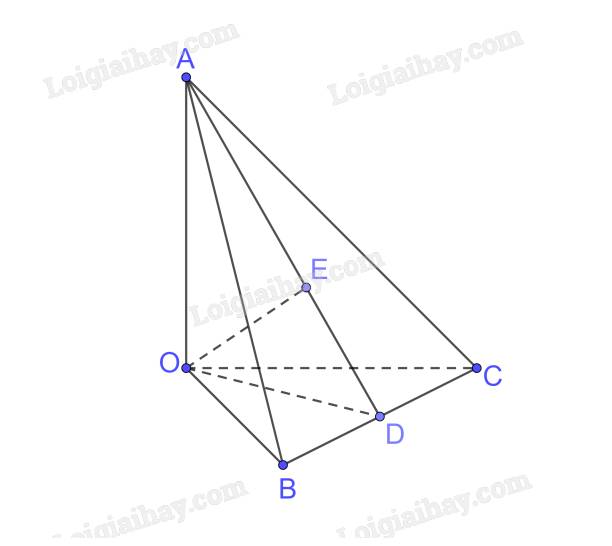
Ta có \(OA \bot OB,OA \bot OC \Rightarrow OA \bot \left( {OBC} \right);BC \subset \left( {OBC} \right) \Rightarrow OA \bot BC\)
Trong (OBC) kẻ \(OD \bot BC\)
\(\begin{array}{l} \Rightarrow BC \bot \left( {OAD} \right);BC \subset \left( {ABC} \right) \Rightarrow \left( {OAD} \right) \bot \left( {ABC} \right)\\\left( {OAD} \right) \cap \left( {ABC} \right) = AD\end{array}\)
Trong (OAD) kẻ \(OE \bot AD\)
\( \Rightarrow OE \bot \left( {ABC} \right) \Rightarrow d\left( {O,\left( {ABC} \right)} \right) = OE\)
Xét tam giác OBC vuông tại O có
\(\frac{1}{{O{D^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}} = \frac{1}{{{{\left( {a\sqrt 2 } \right)}^2}}} + \frac{1}{{{{\left( {2a} \right)}^2}}} = \frac{3}{{4{a^2}}} \Rightarrow OD = \frac{{2a\sqrt 3 }}{3}\)
Xét tam giác OAD vuông tại O có
\(\frac{1}{{O{E^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{D^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{{\left( {\frac{{2a\sqrt 3 }}{3}} \right)}^2}}} = \frac{7}{{4{a^2}}} \Rightarrow OE = \frac{{2a\sqrt 7 }}{7}\)
Vậy \(d\left( {O,\left( {ABC} \right)} \right) = \frac{{2a\sqrt 7 }}{7}\)
Đúng 0
Bình luận (0)