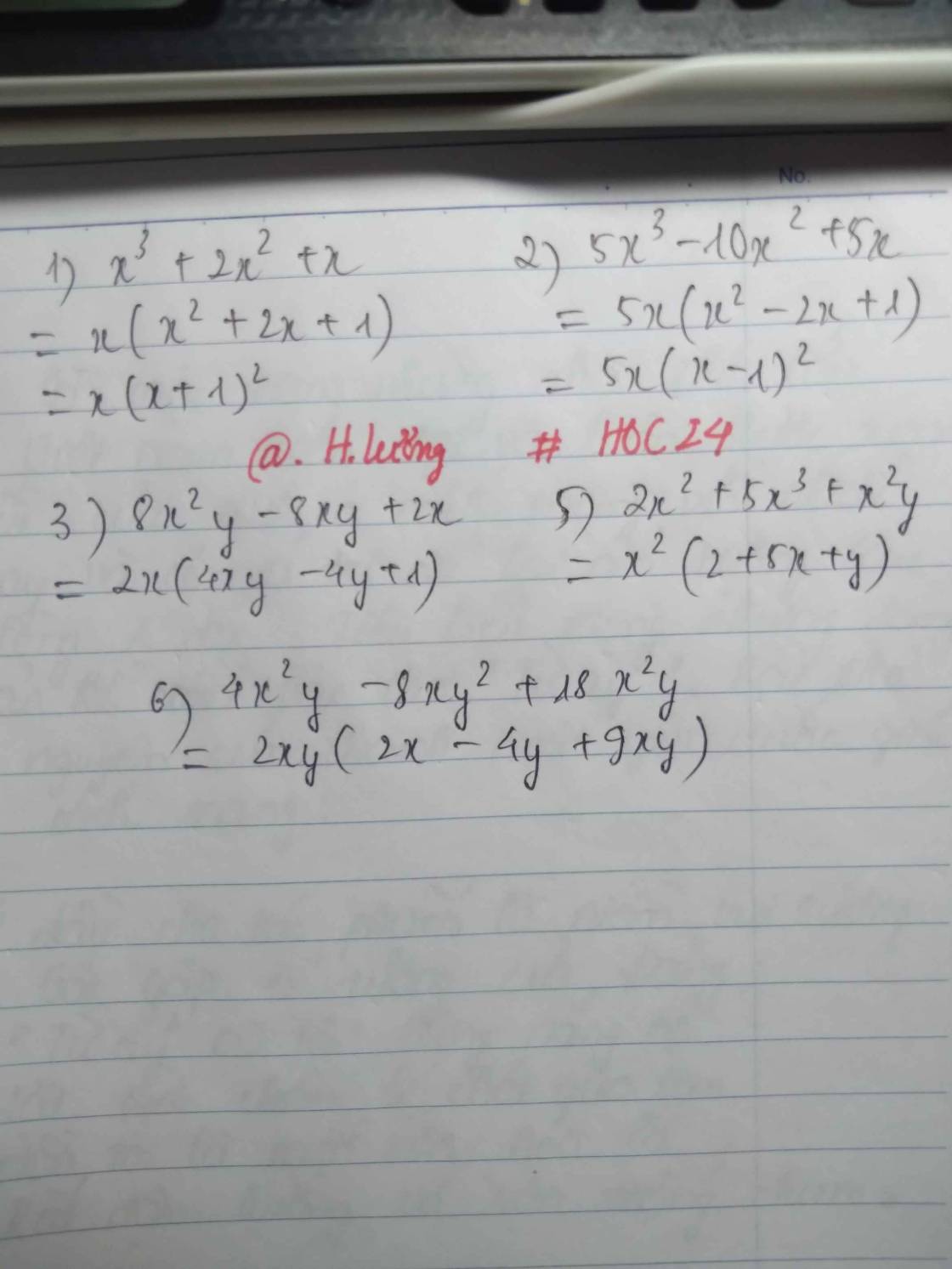là sao ????=))

giữa các phân số là cộng hay trừ vậy???

\(\dfrac{1}{1.3}+\dfrac{1}{2.3}+\dfrac{1}{2.5}+\dfrac{1}{3.5}+\dfrac{1}{3.7}+\dfrac{1}{4.7}+\dfrac{1}{4.9}\) 

\(=\dfrac{1}{1.3}+\dfrac{1}{3.2}+\dfrac{1}{2.5}+\dfrac{1}{5.3}+\dfrac{1}{3.7}+\dfrac{1}{7.4}+\dfrac{1}{4.9}\) 

\(=\left(\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+\dfrac{1}{8.9}\right):\dfrac{1}{2}\) 

\(=\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}\right):\dfrac{1}{2}\) 

\(=\left(\dfrac{1}{2}-\dfrac{1}{9}\right):\dfrac{1}{2}\) 

\(=\dfrac{7}{18}:\dfrac{1}{2}\) 

\(=\dfrac{7}{9}\)

Bạn làm được chưa?

Ta có:

B = (A + B) – A = 2x⁵ + 5x³ – 2 – (x⁴ – 3x² – 2x + 1)

= 2x⁵ + 5x³ – 2 – x⁴ + 3x² + 2x - 1

= 2x⁵ – x⁴ + 5x³ + 3x² + (-2 – 1)

= 2x⁵ – x⁴ + 5x³ + 3x² – 3

C = A – (A – C) = x⁴ – 3x² – 2x + 1 – x³

= x⁴ – x³– 3x² – 2x + 1

Vậy B = 2x⁵ – x⁴ + 5x³ + 3x² – 3

C = x⁴ – x³– 3x² – 2x + 1

\(A=\frac{1}{2.5}+\frac{1}{3.5}+\frac{1}{3.7}+\frac{1}{4.7}+...+\frac{1}{9.19}+\frac{1}{10.19}\)

\(\Rightarrow\frac{1}{2}A=\frac{1}{4.5}+\frac{1}{6.5}+\frac{1}{6.7}+\frac{1}{8.7}+...+\frac{1}{18.19}+\frac{1}{20.19}\)

\(\Rightarrow\frac{1}{2}A=\frac{5-4}{4.5}+\frac{6-5}{6.5}+\frac{7-6}{6.7}+...+\frac{20-19}{20.19}\)

\(\Rightarrow\frac{1}{2}A=\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+...+\frac{1}{19}-\frac{1}{20}\)

\(\Rightarrow\frac{1}{2}A=\frac{1}{4}-\frac{1}{20}\)

\(\Rightarrow\frac{1}{2}A=\frac{1}{5}\)

\(\Rightarrow A=\frac{2}{5}\)

Mình có cách giải khác:

A= \(\frac{1}{2.5}+\frac{1}{3.5}+\frac{1}{3.7}+\frac{1}{4.7}+...+\frac{1}{9.19}+\frac{1}{10.19}\)

A= \(\frac{2.1}{2.2.5}+\frac{2.1}{2.3.5}+\frac{2.1}{2.3.7}+\frac{2.1}{2.4.7}+...+\frac{2.1}{2.9.19}+\frac{2.1}{2.10.19}\)

A= \(\frac{2.1}{4.5}+\frac{2.1}{5.6}+\frac{2.1}{6.7}+\frac{2.1}{7.8}+...+\frac{2.1}{18.19}+\frac{2.1}{19.20}\)

A= \(2.\left(\frac{1}{4.5}+\frac{1}{5.6}+\frac{1}{6.7}+\frac{1}{7.8}+...+\frac{1}{18.19}+\frac{1}{19.20}\right)\)

A=\(2.\left(\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+\frac{1}{7}-\frac{1}{8}+\frac{1}{18}-\frac{1}{19}+\frac{1}{19}-\frac{1}{20}\right)\)

A= \(2.\left(\frac{1}{4}+0+0+0+...+0+0-\frac{1}{20}\right)\)

A=\(2.\left(\frac{1}{4}-\frac{1}{20}\right)\)

A=\(2.\left(\frac{5}{20}-\frac{1}{20}\right)\)

A= \(2.\frac{1}{5}\)

A=\(\frac{2}{5}\)

Xong rùi đó!!!!! :))

1) x³ + 2x² + x

= x(x² + 2x + 1)

= x(x + 1)²

2) 5x³ - 10x² + 5x

= 5x(x² - 2x + 1)

= 5x(x - 1)²

3) 8x²y - 8xy + 2x

= 2x(4xy - 4y + 1)

5) 2x² + 5x³ + x²y

= x²(2 + 5x + y)

6) 4x²y - 8xy² + 18x²y²

= 2xy(2x - 4y + 9xy) 

  Chúc Bạn Học Tốt !

\(A=\dfrac{1}{2.5}+\dfrac{1}{3.5}+\dfrac{1}{3.7}+...+\dfrac{1}{9.19}+\dfrac{1}{10.19}\)

\(A=\dfrac{2}{4.5}+\dfrac{2}{5.6}+\dfrac{2}{6.7}+...+\dfrac{2}{18.19}+\dfrac{2}{19.20}\)

\(A=2.\left(\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+...+\dfrac{1}{18.19}+\dfrac{1}{19.20}\right)\)

\(A=2.\left(\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{19}-\dfrac{1}{20}\right)\)

\(A=2.\left(\dfrac{1}{4}-\dfrac{1}{20}\right)\)

\(A=2.\dfrac{1}{5}\)

\(A=\dfrac{2}{5}\)

Bạn chuyển thành dạng các phân số có tử số bằng 3 bằng cách nhân mỗi phân số với 3 rồi cả tổng tất cả nhân với 1/3. Sau đó làm như bình thường

Ta có:

A\(=\frac{1}{2x5}+\frac{1}{5x3}+\frac{1}{3x7}+\frac{1}{7x4}+...+\frac{1}{14x29}+\frac{1}{29x15}\)

   \(=\frac{2}{2x\left(2x5\right)}+\frac{2}{\left(5x3\right)x2}+\frac{2}{2x\left(3x7\right)}+\frac{2}{\left(7x4\right)x2}+...+\frac{2}{2x\left(14x29\right)}+\frac{2}{\left(29x15\right)x2}\)

   \(=\frac{2}{4x5}+\frac{2}{5x6}+\frac{2}{6x7}+\frac{2}{7x8}+...+\frac{2}{28x29}+\frac{2}{29x30}\)

    \(=2x\left(\frac{1}{4x5}+\frac{1}{5x6}+\frac{1}{6x7}+\frac{1}{7x8}+...+\frac{1}{28x29}+\frac{1}{29x30}\right)\)

     \(=2x\left(\frac{5-4}{4x5}+\frac{6-5}{5x6}+\frac{7-6}{6x7}+\frac{8-7}{7x8}+...+\frac{29-28}{28x29}+\frac{30-29}{29x30}\right)\)

       \(=2x\left(\frac{5}{4x5}-\frac{4}{4x5}+\frac{6}{5x6}-\frac{5}{5x6}+\frac{7}{6x7}-\frac{6}{6x7}+\frac{8}{7x8}-\frac{7}{7x8}+...+\frac{29}{28x29}-\frac{28}{28x29}+\frac{30}{29x30}-\frac{29}{29x30}\right)\)

\(=2x\left(\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+\frac{1}{7}-\frac{1}{8}+...+\frac{1}{28}-\frac{1}{29}+\frac{1}{29}-\frac{1}{30}\right)\)

\(=2x\left(\frac{1}{4}-\left(\frac{1}{5}-\frac{1}{5}\right)-\left(\frac{1}{6}-\frac{1}{6}\right)-...-\left(\frac{1}{28}-\frac{1}{28}\right)-\left(\frac{1}{29}-\frac{1}{29}\right)-\frac{1}{30}\right)\)

\(=2x\left(\frac{1}{4}-0-0-...-0-0-\frac{1}{30}\right)\)

\(=2x\left(\frac{1}{4}-\frac{1}{30}\right)\)

\(=2x\frac{1}{4}-2x\frac{1}{30}\)

\(=\frac{1}{2}-\frac{1}{15}\)

=15/30-2/30=13/30

Thu gọn Q(x) = x4 + 7x2 + 1

Khi đó R(x) = Q(x) - P(x) = 4x2 + 3x + 2. Chọn A