Tập xác định của hàm số f(x) = - x 2 + 2 x x 2 + 1 là tập hợp nào sau đây?
A. ℝ \{-1;1}
B. ℝ
C. ℝ \1}
D. ℝ \{-1}
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Tìm tập xác định của các hàm số sau:
a) \(f(x) = \sqrt {2x + 7} \)
b) \(f(x) = \frac{{x + 4}}{{{x^2} - 3x + 2}}\)
a) Biểu thức \(f(x)\) có nghĩa khi và chỉ khi \(2x + 7 \ge 0,\)tức là khi \(x \ge \frac{{ - 7}}{2}.\)
Vậy tập xác định của hàm số này là \(D = \left[ { - \frac{7}{2}; + \infty )} \right.\)
b) Biểu thức \(f(x)\) có nghĩa khi và chỉ khi \({x^2} - 3x + 2 \ne 0,\)tức là khi \(x \ne 2,x \ne 1.\)
Vậy tập xác định của hàm số này là \(D = \mathbb{R}\backslash \left\{ {1;2} \right\}\)
Cho hàm số bậc hai \(y = f(x) = a{x^2} + bx + c\) có \(f(0) = 1,f(1) = 2,f(2) = 5.\)
a) Hãy xác định giá trị của các hệ số \(a,b\) và \(c.\)
b) Xác định tập giá trị và khoảng biến thiên của hàm số.
Tham khảo:
a) Ta có: \(f(0) = a{.0^2} + b.0 + c = 1 \Rightarrow c = 1.\)
Lại có:
\(f(1) = a{.1^2} + b.1 + c = 2 \Rightarrow a + b + 1 = 2\)
\(f(2) = a{.2^2} + b.2 + c = 5 \Rightarrow 4a + 2b + 1 = 5\)
Từ đó ta có hệ phương trình \(\left\{ \begin{array}{l}a + b + 1 = 2\\4a + 2b + 1 = 5\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}a + b = 1\\4a + 2b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\end{array} \right.\)(thỏa mãn điều kiện \(a \ne 0\))
Vậy hàm số bậc hai đó là \(y = f(x) = {x^2} + 1\)
b) Tập giá trị \(T = \{ {x^2} + 1|x \in \mathbb{R}\} \)
Vì \({x^2} + 1 \ge 1\;\forall x \in \mathbb{R}\) nên \(T = [1; + \infty )\)
Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.1}} = 0;{y_S} = f(0) = 1\)
Hay \(S\left( {0;1} \right).\)
Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:

Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\)
Cho hàm số f(x)= x+2/x-1
Tìm tập xác định của f(x)
Tìm tập xác định của các hàm số sau:
a) \(f(x) = \sqrt { - 5x + 3} \)
b) \(f(x) = 2 + \frac{1}{{x + 3}}\)
a) Biểu thức \(f(x)\) có nghĩa khi và chỉ khi \( - 5x + 3 \ge 0,\)tức là khi \(x \le \frac{3}{5}.\)
Vậy tập xác định của hàm số này là \(D = ( - \infty ;\frac{3}{5}]\)
b) Biểu thức \(f(x)\) có nghĩa khi và chỉ khi \(x + 3 \ne 0,\)tức là khi \(x \ne - 3\)
Vậy tập xác định của hàm số này là \(D = \mathbb{R}\backslash \left\{ { - 3} \right\}\)
tìm tập xác định của hàm số y=f(x) = \(\sqrt{3-x}+\sqrt{7x^2-x-6}\)
ĐKXĐ: \(\left\{{}\begin{matrix}3-x\ge0\\7x^2-x-6\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le3\\\left[{}\begin{matrix}x\ge1\\x\le-\dfrac{6}{7}\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x\le-\dfrac{6}{7}\\1\le x\le3\end{matrix}\right.\)
Tìm tập xác định của hàm số y = f(x) = x\(^2\)và tính f(-2)
TXĐ: D=R
\(f\left(-2\right)=\left(-2\right)^2=4\)
cho hàm số y =f(x) =\(\left\{{}\begin{matrix}\dfrac{2}{x-1}\\\sqrt{x+1}\\x^{2^{ }}-1\end{matrix}\right.\)
khi x< 0 ; khi 0 ≤ x ≤ 2 ; khi x>2
a. Tìm tập xác định của hàm số.
b. Tính f(-1), f(0), f(1), f(2), f(3).
a: TXĐ: D=R
b: \(f\left(-1\right)=\dfrac{2}{-1-1}=\dfrac{2}{-2}=-1\)
\(f\left(0\right)=\sqrt{0+1}=1\)
\(f\left(1\right)=\sqrt{1+1}=\sqrt{2}\)
\(f\left(2\right)=\sqrt{3}\)
Cho hàm số y=f(x) xác định bởi công thức: \(y=\frac{-18}{\left|2x-1\right|}\)
a) Tìm đk xác định và tập xác định của hàm số.
b) Biết \(x\in\left\{-4;-2;-1;0;1;2;3\right\}\). Hãy viết tập hợp các cặp số xác định bởi hàm số y=f(x)
Câu a mình làm đc r, nhờ m.n làm hộ mình câu b và ý nhỏ này nx nhé, cũng nằm trong bài.
c) Tìm \(x\in Z\) để hàm số y=f(x) đạt GTNN? Tính giá trị đó.
Tìm tập xác định của hàm số
\(y=f\left(x\right)=\dfrac{\sqrt{4\pi^2-x^2}}{cos\left(x\right)}\)
Hàm số xác định khi: \(\left\{{}\begin{matrix}4\pi^2-x^2\ge0\\cosx\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2\pi\le x\le2\pi\\x\ne\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)
Cho hàm số y = f(x) xác định trên D = − 1 ; + ∞ \ 1 . Dưới đây là một phần đồ thị của y = f(x)
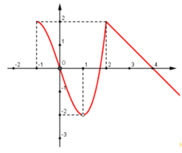
Hỏi trong các mệnh đề sau, có bao nhiêu mệnh đề đúng:
(I) Số điểm cực đại của hàm số trên tập xác định là 1.
(II) Hàm số có cực tiểu là -2 tại x = 1
(III) Hàm số đạt cực đại tại x = 2
(IV) Hàm số đạt cực đại tại x = -1
A. 0
B. 1
C. 2
D. 3

Hình ảnh trên là một phần đồ thị của y trên tập xác định. Ta thấy rằng hàm số đạt cực đại tại x = 2 nhưng không chắc rằng có còn điểm cực đại nào khác trên những khoảng rộng hơn hay không (I) sai, (III) đúng.
Hàm số không xác định tại x = 1 nên không thể đạt cực tiểu tại điểm này =>(II) sai.
Chọn B