Số nghiệm của phương trình l o g 4 x 2 + l o g 8 ( x - 6 ) 3 = l o g 2 7
A. 0
B. 1
C. 3
D. 2
1) Số nghiệm của phương trình\(\dfrac{5x}{x-3}-\dfrac{x+2}{x+3}=2\) là ?
2) Diện tích hình thang vuông có một góc bằng 45o; độ dài hai đáy lần lượt là 4cm và 6cm là .............. cm vuông ?
3) Nghiệm không nguyên của phương trình \(8\cdot\left(x^2+\dfrac{1}{x^2}\right)-34\cdot\left(x+\dfrac{1}{x}\right)+51=0\) là x = ?
4) Nghiệm lớn nhất của phương trình (x - 1)2 + Ix + 21I - x2 - 5 = 0 là x = ? (Câu này 17 đúng không ạ ??)
Akai Haruma @@ em cần sự giúp đỡ @@
Bài 1:
\(\Leftrightarrow\dfrac{5x^2+15x-\left(x+2\right)\left(x+3\right)}{x^2-9}=2\)
\(\Leftrightarrow\dfrac{5x^2+15x-\left(x^2+5x+6\right)-2x^2+18}{\left|x\right|\ne3}=0\)
\(\Leftrightarrow2x^2-10x+12=0\)
\(\left(x+2\right)\left(x+6\right)=0\Rightarrow\left[{}\begin{matrix}x=-2\\x=-6\end{matrix}\right.\) khác +-3 => kết luận hai nghiệm
Bài 4: tìm nghiệm lớn => xét x>-21
\(x^2-2x+1+x+21-x^2-5=0\)
\(\Leftrightarrow x=-5+22=17\Rightarrow x=17\) >-21 nhận
Bài 3
đặt x+1/x= t => !t!>2
\(8\left(t^2-2\right)-34t+51=0\)
\(8t^2-34t+35=0\)
\(t^2-\dfrac{34}{8}t+\dfrac{17^2}{8^2}=\dfrac{17^2}{8^2}-\dfrac{35}{8}=\dfrac{9}{8^2}\)
\(\left[{}\begin{matrix}t=\dfrac{17-3}{8}=\dfrac{14}{8}=\dfrac{7}{4}\left(l\right)\\t=\dfrac{17+3}{8}=\dfrac{20}{8}=\dfrac{5}{2}\end{matrix}\right.\)
Thay t=5/2 vào tính x :\(x^2-\dfrac{5}{2}x+\dfrac{25}{4}=\dfrac{25}{16}-1=\dfrac{9}{16}\)
\(\left[{}\begin{matrix}x=\dfrac{5-3}{4}=\dfrac{1}{2}\left(n\right)\\x=\dfrac{5+3}{4}=2\left(l\right)\end{matrix}\right.\)
Kết luận: x=1/2
Cho hàm số f(x) = log2x và g(x) = log2(4-x) . Tìm tập nghiệm của bất phương trình f(x + 1) < g(x + 2)
A. S = - ∞ ; 1 2
B. S = - 1 ; 1 2
C. S = (0; 2).
D. S = - ∞ ; 2
Chọn B.
Ta có: f(x + 1) = log2(x + 1) và g(x + 2) = log2(2 - x)
![]()
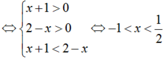
Giúp mk với, các cậu ơi!!! Giải chi tiết giúp mk nha!
Câu 1: Hãy viết nghiệm tổng quát và biểu diễn tập nghiệm của các phương trình sau:
a) 3x – y = 2
b) 2x + y = 5
c) 4x + 0y = -2
d) 0x + 2y = -4
Gợi ý: Sử dụng kiến thức bài 1(chương III )
Câu 2: Mỗi quả lê giá năm đồng, mỗi quả táo giá bảy đồng. Số tiền mua cả lê và táo là 35 đồng
1) Viết phương trình biểu thị số tiền mua lê và táo?
2) Dạng tổng quát phương trình trên là gì ? Xác định các hệ số?
3) Viết nghiệm tổng quát của phương trình trên?
4) Vẽ minh họa tập nghiệm của phương trình trên?
5) Xác định số quả lê và số quả táo tương ứng có thể mua?
số nào dưới đây là nghiệm của phương trình x2 - 6 = x nhưng ko là nghiệm của phương trình x2 - 3x - 10 = 0
A. -2 B. 5 C. 4 D. 3
*) x2 - 6 = x (1)
\(\Leftrightarrow\) x2 - x - 6 = 0
\(\Leftrightarrow\) x2 - 3x + 2x - 6 = 0
\(\Leftrightarrow\) x(x - 3) + 2(x - 3) = 0
\(\Leftrightarrow\) (x - 3)(x + 2) = 0
\(\Leftrightarrow\) x - 3 = 0 hoặc x + 2 = 0
\(\Leftrightarrow\) x = 3 và x = -2
Vậy S = {3; -2}
*) x2 - 3x - 10 = 0 (2)
\(\Leftrightarrow\) x2 - 5x + 2x - 10 = 0
\(\Leftrightarrow\) x(x + 2) - 5(x + 2) = 0
\(\Leftrightarrow\) (x + 2)(x - 5) = 0
\(\Leftrightarrow\) x + 2 = 0 hoặc x - 5 = 0
\(\Leftrightarrow\) x = -2 và x = 5
Vậy S = {-2; 5}
Vậy pt là nghiệm của pt (1) nhưng ko phải nghiệm của pt (2) là 3
Vậy phương án đúng là D
Chúc bn học tốt!!
Bài 1
\(\Leftrightarrow\left(x-4\right)\left(x+2\right)=4\sqrt{-\left(x-4\right)\left(x+2\right)}\)
\(\Leftrightarrow\sqrt{-16\left(x-4\right)\left(x+2\right)}=\left(x-4\right)\left(x+2\right)\)
\(\Leftrightarrow-16\left(x-4\right)\left(x+2\right)=\left(x-4\right)^2\cdot\left(x+2\right)^2\)
\(\Leftrightarrow\left(x-4\right)\left(x+2\right)=0\)
=>x=4 hoặc x=-2
=>Số nghiệm là 2 nghiệm
Phương pháp độc đáo nhất của Menden là gì?
Phương pháp đó đc làm ra sao?
Menden đã thí nghiệm như thế nào?
Đậu đc ông thí nghiệm thành công là đậu gì?
Nó có đặc tính ra sao?
- Phương pháp độc đáo nhất của Menđen là phương pháp phân tích các thế hệ lai
-đậu đc ông thí nghiệm là đậu Hà Lan
- các đặc tính:
+ thời gian sinh trưởng, phát triển ngắn
+ có nhiều tính trạng đối lập
+ có khả năng tự thụ phấn cao
Cho đa thức ƒ (x)=2x^2−x; g(x)=mx^2+2m+1
a) Tính ƒ (x) g(x);ƒ (x)−g(x)
b) Tìm m để h(x)=ƒ (x) g(x)có bậc là 1
c) Với giá trị nào của m để h(x)có bậc là 2
d) Có giá trị nào của m để h(x) có nghiệm là x=2
1. Số nào sau đây là nghiệm của đa thức f(x) = \(\frac{2}{3}\)x + 1
A. \(\frac{2}{3}\) B. \(\frac{2}{3}\) C. -\(\frac{3}{2}\) D. -\(\frac{2}{3}\)
2. Đa thức g(x) = x2 + 1
A. Ko có nghiệm B. Có nghiệm là -1
C. Có nghiệm là 1 D. Có 2 nghiệm
3. Độ dài 2 cạnh góc vuông liên tiếp lần lượt là 3cm và 4cm thì độ dài cạnh huyền là:
A. 5 B. 7 C. 6 D. 14
4. Tâm giác có 1 góc 60o thì với điều kiện nào thì trở thành tam giác đều:
A. 2 cạnh = nhau B. 3 góc nhọn C. 2 góc nhọn D. 1 cạnh đáy
5. Nếu AM là đường trung tuyến và G là trọng tâm của ΔABC thì:
A. AM = AB B. AG = \(\frac{2}{3}\)AM C. AG = \(\frac{3}{4}\)AB D. AM = AG
cho g(x) = x^2 - 3x - 4 Giá trị nào sau đây của x là 1 nghiệm của đa thức g(x)?
A x = 0
B x = 1
C X = 3
D x = -1
nêu cách làm giúp mik nhoa
\(g\left(x\right)=x^2-3x-4\)
cách 1
thay lần lượt x vào g(x) xem cái nào =0 thì nhận
\(g\left(a\right)=g\left(0\right)=0^2-30-4=-4\) loại
\(g\left(b\right)=g\left(1\right)=1^2-3.1-4=-6\) loại
\(g\left(c\right)=g\left(3\right)=3^2-3.3-4=-4\)loiaj
g(d) không tính nũa vì còn duy nhát => chọn (D)
cách 2
Tìm nghiệm g(x) nghĩa là chưa quan tâm đến đáp án
\(g\left(x\right)=x^2-3x-4=\left(x^2+x\right)-\left(4x+4\right)=x\left(x+1\right)-4\left(x+1\right)=\left(x+1\right)\left(x-4\right)\)\(g\left(x\right)=0\Rightarrow\left(x+1\right)\left(x-4\right)=0\Rightarrow\left[{}\begin{matrix}x+1=0\\x-4=0\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=-1\\x=4\end{matrix}\right.\)
Giờ mới để ý đến đáp án => PA(D)
cách 3
siêu tốc (đối với lớp 7)
g(1) =1-3-4 => g(-1) =1+3-4 =0 => x=-1 là nghiệm
=> PA(D)
Phương trình \(\sqrt{2-f\left(x\right)}=f\left(x\right)\) có tập nghiệm A = {1;2;3}. Phương trình \(\sqrt{2.g\left(x\right)-1}+\sqrt[3]{3.g\left(x\right)-2}=2.g\left(x\right)\) có tập nghiệm là B = {0;3;4;5} . Hỏi tập nghiệm của phương trình \(\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+f\left(x\right).g\left(x\right)+1=f\left(x\right)+g\left(x\right)\)
có bao nhiêu phần tử?
A.1
B.4 C.6 D.7
\(\sqrt{2-f\left(x\right)}=f\left(x\right)\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)\ge0\\f^2\left(x\right)+f\left(x\right)-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=1\\f\left(x\right)=-2< 0\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow f\left(1\right)=f\left(2\right)=f\left(3\right)=1\)
\(\sqrt{2g\left(x\right)-1}+\sqrt[3]{3g\left(x\right)-2}=2.g\left(x\right)\)
\(VT=1.\sqrt{2g\left(x\right)-1}+1.1\sqrt[3]{3g\left(x\right)-2}\)
\(VT\le\dfrac{1}{2}\left(1+2g\left(x\right)-1\right)+\dfrac{1}{3}\left(1+1+3g\left(x\right)-2\right)\)
\(\Leftrightarrow VT\le2g\left(x\right)\)
Dấu "=" xảy ra khi và chỉ khi \(g\left(x\right)=1\)
\(\Rightarrow g\left(0\right)=g\left(3\right)=g\left(4\right)=g\left(5\right)=1\)
Để các căn thức xác định \(\Rightarrow\left\{{}\begin{matrix}f\left(x\right)-1\ge0\\g\left(x\right)-1\ge0\end{matrix}\right.\)
Ta có:
\(\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+f\left(x\right).g\left(x\right)-f\left(x\right)-g\left(x\right)+1=0\)
\(\Leftrightarrow\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+\left[f\left(x\right)-1\right]\left[g\left(x\right)-1\right]=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=1\\g\left(x\right)=1\end{matrix}\right.\) \(\Leftrightarrow x=3\)
Vậy tập nghiệm của pt đã cho có đúng 1 phần tử