Xét dãy số ( u n ) , n ∈ N * được xác định bởi u 1 = 3 u n + 1 = 1 2 u n . Tìm u 10
A. u 10 = 3 512
B. u 10 = 3 1024
C. u 10 = 1 1024
D. u 10 = 1 512
a) Xét dãy số \(\left( {{u_n}} \right)\) với \({u_n} = 3n - 1\). Tính \({u_{n + 1}}\) và so sánh với \({u_n}\).
b) Xét dãy số \(\left( {{v_n}} \right)\) với \({v_n} = \frac{1}{{{n^2}}}\). Tính \({v_{n + 1}}\) và so sánh với \({v_n}\).
a) Ta có: \({u_{n + 1}} = 3\left( {n + 1} \right) - 1 = 3n + 2\).
Suy ra \({u_{n + 1}} > {u_n}\).
b) Ta có: \({v_{n + 1}} = \frac{1}{{{{\left( {n + 1} \right)}^2}}}\).
Suy ra: \({u_{n + 1}} < {u_n}\).
Xét tính đơn điệu của dãy số sau:
a) un=\(\dfrac{\sqrt{n+1}-n}{n}\)
Cho dãy số ( x n ) : x 0 = 1 x n = 2 n ( n - 1 ) 2 ∑ i = 1 n - 1 x i , n = 2 , 3 . . . . . Xét dãy số yn = xn+1 - xn. Khẳng định nào đúng về dãy (yn)
A. Tăng, bị chặn
B. Giảm, bị chặn
C. Tăng, chặn dưới
D. Giảm, chặn trên
Chọn A.
Ta có: 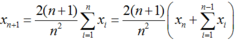
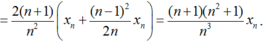
Do đó: 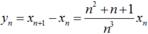
- Ta chứng minh dãy (yn) tăng.
Ta có: 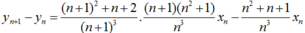
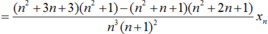
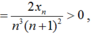
- Ta chứng minh dãy (yn) bị chặn.
Trước hết ta chứng minh: xn ≤ 4(n – 1) (1)
* Với n = 2, ta có: x2 = 4x1 = 4 nên (1) đúng với n = 2
* Giả sử (1) đúng với n, tức là: xn ≤ 4(n – 1), ta có
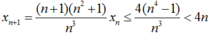
Nên (1) đúng với n + 1. Theo nguyên lí quy nạp ta suy ra (1) đúng
Ta có: 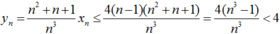
Vậy bài toán được chứng minh.
Viết chương trình pascal nhập dãy số n (n nhập từ bàn phím) thực hiện
+ dòng 1 xuất ra màn hình dãy số vừa nhập
+ dòng 2 tổng của dãy số vừa nhập và xét tổng đó có phải là số nguyên tố không ?
+ dòng 3 các số ở vị trí lẻ của dãy số và tổng của nó. Xét tổng đó có phải là số chính phương không?
+ dòng 4 các số ở vị trí chẵn của dãy số và tổng của chúng. Xét tổng đó có phải là số hoàn hảo không ?
+ dòng 5 số lớn nhất và số nhỏ nhất của dãy số và tổng của hai số đó Giúp với !!
uses crt;
var a:array[1..100]of integer;
i,n,t,t1,t2,t3,min,max:integer;
kt:boolean;
begin
clrscr;
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
writeln('Day so ban vua nhap la: ');
for i:=1 to n do
write(a[i]:4);
writeln;
t:=0;
for i:=1 to n do
t:=t+a[i];
kt:=true;
for i:=2 to trunc(sqrt(t)) do
if t mod i=0 then
begin
kt:=false;
break;
end;
writeln('Tong cua day so la: ',t);
if (kt=true) and (t>1) then writeln(t,' la so nguyen to')
else writeln(t,' khong la so nguyen to');
writeln('Cac so o vi tri le cua day so la: ');
t1:=0;
for i:=1 to n do
if i mod 2=1 then
begin
write(a[i]:4);
t1:=t1+a[i];
end;
writeln;
writeln('Tong cac so o vi tri le cua day so la: ',t1);
if trunc(sqrt(t1))=sqrt(t1) then writeln(t1,' la so chinh phuong')
else writeln(t1,' khong la so chinh phuong');
writeln('Cac so o vi tri chan cua day so la: ');
t2:=0;
for i:=1 to n do
if i mod 2=0 then
begin
write(a[i]:4);
t2:=t2+a[i];
end;
writeln;
writeln('Tong cac so o vi tri chan cua day so la: ',t2);
t3:=0;
for i:=1 to t2 do
if t2 mod i=0 then t3:=t3+i;
if t3=t2 then writeln(t2,' la so hoan hao')
else writeln(t2,' khong la so hoan hao');
max:=a[1];
min:=a[1];
for i:=1 to n do
begin
if max<a[i] then max:=a[i];
if min>a[i] then min:=a[i];
end;
writeln('So lon nhat cua day la: ',max);
writeln('So nho nhat cua day la: ',min);
writeln('Tong cua so lon nhat va so nho nhat la: ',max+min);
readln;
end.
uses crt;
var a:array[1..100]of integer;
n,i,t,kt,j,t1,t2,t3,max,min:integer;
begin
clrscr;
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
writeln('Day so ban vua nhap la: ');
for i:=1 to n do
write(a[i]:4);
writeln;
t:=0;
for i:=1 to n do
t:=t+a[i];
writeln('Tong cua day so vua nhap la: ',t);
kt:=0;
for i:=2 to trunc(sqrt(t)) do
if t mod i=0 then
begin
kt:=1;
break;
end;
if (kt=0) and (t>1) then writeln(t,' la so nguyen to');
else writeln(t,' khong la so nguyen to');
t1:=0;
writeln('Cac so o vi tri le cua day la: ');
for i:=1 to n do
if i mod 2=1 then
begin
write(a[i]:4);
t1:=t1+a[i];
end;
writeln;
writeln('Tong cac so o vi tri le la: ',t1);
if trunc(sqrt(t1))=sqrt(t1) then writeln(t1,' la so chinh phuong')
else writeln(t1,' khong la so chinh phuong');
t2:=0;
writeln('Cac so o vi tri chan la: ');
for i:=1 to n do
if i mod 2=0 then
begin
write(a[i]:4);
t2:=t2+a[i];
end;
writeln;
writeln('Tong cac so o vi tri chan la: ',t2);
t3:=0;
for i:=1 to t2 do
if t2 mod i=0 then t3:=t3+i;
if t3=t2 then writeln(t2,' la so hoan hao')
else writeln(t2,' khong la so hoan hao');
max:=a[1];
min:=a[1];
for i:=1 to n do
begin
if max<a[i] then max:=a[i];
if min>a[i] then min:=a[i];
end;
writeln('Gia tri lon nhat la: ',max);
writeln('Gia tri nho nhat la: ',min);
writeln('Tong cua hai so lon nhat va nho nhat la: ',max+min);
readln;
end.
xét tính bị chặn của dãy số un=\(n^2-\sqrt{n^2+1}\)
Bạn xem lại xem viết đề có thiếu/nhầm gì không?
xét tính tăng, giảm của các dãy số sau
\(u_n=\dfrac{n+2}{n}\)
\(u_n=\dfrac{n+2}{n}\)
\(u_{n+1}=\dfrac{n+3}{n+1}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{n+3}{n+1}-\dfrac{n+2}{n}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{n\left(n+3\right)-\left(n+1\right)\left(n+2\right)}{n\left(n+1\right)}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{n^2+3n-\left(n^2+3n+2\right)}{n\left(n+1\right)}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{n^2+3n-n^2-3n-2}{n\left(n+1\right)}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{-2}{n\left(n+1\right)}< 0\)
Vậy dãy số \(u_n\) đã cho là dãy giảm
Xét tính tăng giảm của dãy số: un = \(\sqrt{n+10}-\sqrt{n+2}\)
\(u_n=\sqrt[]{n+10}-\sqrt[]{n+2}\)
\(\Leftrightarrow u_n=\dfrac{n+10-\left(n+2\right)}{\sqrt[]{n+10}+\sqrt[]{n+2}}\)
\(\Leftrightarrow u_n=\dfrac{8}{\sqrt[]{n+10}+\sqrt[]{n+2}}\)
\(u_{n+1}=\sqrt[]{n+11}-\sqrt[]{n+3}\)
\(\Leftrightarrow u_{n+1}=\dfrac{n+11-\left(n+3\right)}{\sqrt[]{n+11}+\sqrt[]{n+3}}\)
\(\Leftrightarrow u_{n+1}=\dfrac{8}{\sqrt[]{n+11}+\sqrt[]{n+3}}\)
\(u_{n+1}-u_n=8\left(\dfrac{1}{\sqrt[]{n+11}+\sqrt[]{n+3}}-\dfrac{1}{\sqrt[]{n+10}+\sqrt[]{n+2}}\right)\)
mà \(\dfrac{1}{\sqrt[]{n+11}+\sqrt[]{n+3}}< \dfrac{1}{\sqrt[]{n+10}+\sqrt[]{n+2}}\)
\(\Rightarrow u_{n+1}-u_n< 0\)
Vậy dãy đã cho là dãy số giảm
Xét tính tăng giảm của dãy số: un = \(\dfrac{3^n-1}{2^n}\)
\(u_n=\dfrac{3^n-1}{2^n}\)
\(\Rightarrow u_{n+1}=\dfrac{3^{n+1}-1}{2^{n+1}}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{3^{n+1}-1}{2^{n+1}}-\dfrac{3^n-1}{2^n}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{2^n.3^{n+1}-2^n-2^{n+1}.3^n+2^{n+1}}{2^n.2^{n+1}}\)
\(=\dfrac{2^n.3^n\left(3-2\right)-2^n\left(2-1\right)}{2^{2n+1}}\)
\(=\dfrac{2^n.\left(3^n-1\right)}{2^{2n+1}}\)
\(=\dfrac{\left(3^n-1\right)}{2}>0\left(n>1\right)\)
Vậy dãy \(u_n\)đã cho tăng
Cho dãy số 1,1/2,1/3,…,1/n. Xét tính bị chặn của dãy số đó?
A. Dãy số không bị chặn cả trên và dưới
B. Dãy số bị chặn trên
C. Dãy số bị chặn dưới
D. Dãy số bị chặn