Xét hai dãy số u n , v n , n ∈ N * được xác định bởi u 1 = 1 , v 1 = 2 , u n + 1 = u n + 1 v n , v n + 1 = v n + 1 u n . Đặt S = u 10 + v 10 . Khẳng định nào sau đây là đúng?
A. S < 4 5
B. S < 2 5
C. S > 4 5
D. S > 8 5
Những câu hỏi liên quan
Cho một dãy số nguyên A gồm N phần tử A1, A2,…, AN và hai số nguyên dương U, V (1 ≤ U ≤ V ≤ N). Hãy tìm một đoạn con liên tiếp của dãy A có tổng các phần tử đạt giá trị lớn nhất và độ dài là D tùy ý với U ≤ D ≤ V. (Độ dài của đoạn con là số lượng phần tử trên đoạn con đó).input out5 12 3 -4 3 -2 -6 5giúp em với c++ ạ
Đọc tiếp
Cho một dãy số nguyên A gồm N phần tử A1, A2,…, AN và hai số nguyên dương U, V (1 ≤ U ≤ V ≤ N). Hãy tìm một đoạn con liên tiếp của dãy A có tổng các phần tử đạt giá trị lớn nhất và độ dài là D tùy ý với U ≤ D ≤ V. (Độ dài của đoạn con là số lượng phần tử trên đoạn con đó).
input out
5 1
2 3 -4 3 -2 -6 5
giúp em với c++ ạ
a) Xét dãy số \(\left( {{u_n}} \right)\) với \({u_n} = 3n - 1\). Tính \({u_{n + 1}}\) và so sánh với \({u_n}\).
b) Xét dãy số \(\left( {{v_n}} \right)\) với \({v_n} = \frac{1}{{{n^2}}}\). Tính \({v_{n + 1}}\) và so sánh với \({v_n}\).
a) Ta có: \({u_{n + 1}} = 3\left( {n + 1} \right) - 1 = 3n + 2\).
Suy ra \({u_{n + 1}} > {u_n}\).
b) Ta có: \({v_{n + 1}} = \frac{1}{{{{\left( {n + 1} \right)}^2}}}\).
Suy ra: \({u_{n + 1}} < {u_n}\).
Đúng 0
Bình luận (0)
Xét tính đơn điệu của dãy số sau:
a) un=\(\dfrac{\sqrt{n+1}-n}{n}\)
Cho dãy số
(
x
n
)
:
x
0
1
x
n
2
n
(...
Đọc tiếp
Cho dãy số ( x n ) : x 0 = 1 x n = 2 n ( n - 1 ) 2 ∑ i = 1 n - 1 x i , n = 2 , 3 . . . . . Xét dãy số yn = xn+1 - xn. Khẳng định nào đúng về dãy (yn)
A. Tăng, bị chặn
B. Giảm, bị chặn
C. Tăng, chặn dưới
D. Giảm, chặn trên
Chọn A.
Ta có: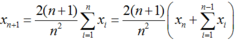 
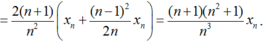
Do đó: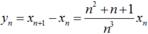 
- Ta chứng minh dãy (yn) tăng.
Ta có: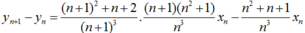 
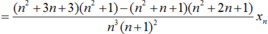
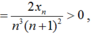
- Ta chứng minh dãy (yn) bị chặn.
Trước hết ta chứng minh: xn ≤ 4(n – 1) (1)
* Với n = 2, ta có: x2 = 4x1 = 4 nên (1) đúng với n = 2
* Giả sử (1) đúng với n, tức là: xn ≤ 4(n – 1), ta có
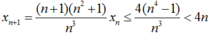
Nên (1) đúng với n + 1. Theo nguyên lí quy nạp ta suy ra (1) đúng
Ta có: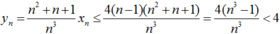 
Vậy bài toán được chứng minh.
Đúng 0
Bình luận (0)
xét tính bị chặn của dãy số un=\(n^2-\sqrt{n^2+1}\)
Bạn xem lại xem viết đề có thiếu/nhầm gì không?
Đúng 1
Bình luận (0)
Xét tính tăng giảm của dãy số: un = \(\sqrt{n+10}-\sqrt{n+2}\)
\(u_n=\sqrt[]{n+10}-\sqrt[]{n+2}\)
\(\Leftrightarrow u_n=\dfrac{n+10-\left(n+2\right)}{\sqrt[]{n+10}+\sqrt[]{n+2}}\)
\(\Leftrightarrow u_n=\dfrac{8}{\sqrt[]{n+10}+\sqrt[]{n+2}}\)
\(u_{n+1}=\sqrt[]{n+11}-\sqrt[]{n+3}\)
\(\Leftrightarrow u_{n+1}=\dfrac{n+11-\left(n+3\right)}{\sqrt[]{n+11}+\sqrt[]{n+3}}\)
\(\Leftrightarrow u_{n+1}=\dfrac{8}{\sqrt[]{n+11}+\sqrt[]{n+3}}\)
\(u_{n+1}-u_n=8\left(\dfrac{1}{\sqrt[]{n+11}+\sqrt[]{n+3}}-\dfrac{1}{\sqrt[]{n+10}+\sqrt[]{n+2}}\right)\)
mà \(\dfrac{1}{\sqrt[]{n+11}+\sqrt[]{n+3}}< \dfrac{1}{\sqrt[]{n+10}+\sqrt[]{n+2}}\)
\(\Rightarrow u_{n+1}-u_n< 0\)
Vậy dãy đã cho là dãy số giảm
Đúng 2
Bình luận (0)
xét tính tăng, giảm của các dãy số sau
\(u_n=\dfrac{n+2}{n}\)
\(u_n=\dfrac{n+2}{n}\)
\(u_{n+1}=\dfrac{n+3}{n+1}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{n+3}{n+1}-\dfrac{n+2}{n}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{n\left(n+3\right)-\left(n+1\right)\left(n+2\right)}{n\left(n+1\right)}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{n^2+3n-\left(n^2+3n+2\right)}{n\left(n+1\right)}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{n^2+3n-n^2-3n-2}{n\left(n+1\right)}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{-2}{n\left(n+1\right)}< 0\)
Vậy dãy số \(u_n\) đã cho là dãy giảm
Đúng 1
Bình luận (0)
Xét tính tăng giảm của dãy số: un = \(\dfrac{3^n-1}{2^n}\)
\(u_n=\dfrac{3^n-1}{2^n}\)
\(\Rightarrow u_{n+1}=\dfrac{3^{n+1}-1}{2^{n+1}}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{3^{n+1}-1}{2^{n+1}}-\dfrac{3^n-1}{2^n}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{2^n.3^{n+1}-2^n-2^{n+1}.3^n+2^{n+1}}{2^n.2^{n+1}}\)
\(=\dfrac{2^n.3^n\left(3-2\right)-2^n\left(2-1\right)}{2^{2n+1}}\)
\(=\dfrac{2^n.\left(3^n-1\right)}{2^{2n+1}}\)
\(=\dfrac{\left(3^n-1\right)}{2}>0\left(n>1\right)\)
Vậy dãy \(u_n\)đã cho tăng
Đúng 2
Bình luận (0)
Xét hai dãy số
(
u
n
)
,
(
v
n
)
,
n
∈
N
*
,
được xác định bởi
u
1
1...
Đọc tiếp
Xét hai dãy số ( u n ) , ( v n ) , n ∈ N * , được xác định bởi u 1 = 1 , v 1 = 2 , u n + 1 = u n + 1 v n , v n + 1 = v n + 1 u n . Đặt S = u 10 + v 10 . Khẳng định nào sau đây là đúng?
A. S < 4 5
B. S < 2 5
C. S > 4 5
D. S > 8 5
Đáp án C
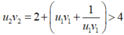
⇒ u 3 v 3 > 6
Bằng quy nạp ta chỉ ra được
Đúng 0
Bình luận (0)