toán nâng siêu nâng cao
Các cậu ơi gửi cho tớ mấy bài toán nâng cao siêu khó siêu khổng lồ về tiên đề ơ-cilt về 2 đường thẳng song song nhé
Bài 1:
Trên hình dưới, hai đường thẳng a, b song song với nhau, đường thẳng c cắt a tại A, cắt b tại B.
a) Lấy một cặp góc so le trong (chẳng hạn cặp góc A4,B1A4,B1) rồi đo xem hai góc đó có bằng nhau hay không?
b) Hãy lí luận vì sao ˆA4=ˆB1A4^=B1^ theo gợi ý sau:
- Nếu ˆA4≠ˆB1A4^≠B1^ thì qua A ta vẽ tia Ap sao cho ˆPAB=ˆB1.PAB^=B1^.
- Thế thì AP // b, vì sao?
- Qua A, vừa có a // b, vừa có AP // b, thì sao?
Kết luận: Đường thẳng AP và đường thẳng a chỉ là một. Nói cách khác, ˆPAB=ˆA4PAB^=A4^ từ đó ˆA4=ˆB1.A4^=B1^.
Chứng minh N=(a-2).(a+3)-(a-3).(a+2)là số chẵn, trong đó a thuộc Z.
Siêu nâng cao toán 6 nhé!
Giải
Xét a chẵn, a có dạng 2k (k thuộc Z)
Ta có N = (a-2).(a+3)-(a-3).(a+2)=(2k-2).(2k+3)-(2k-3).(2k+2)=2(k-1).(2k+3)-(2k-3).2(k+1)=2[(k-1).(2k+3)-(2k-3).(k+1)] chia hết cho 2
=> N là số chẵn (1)
Xét a lẻ, a có dạng 2k+1 (k thuộc Z)
Ta có N = (a-2).(a+3)-(a-3).(a+2)=(2k+1-2).(2k+1+3)-(2k+1-3).(2k+1+2)=(2k-1).(2k+4)-(2k-2).(2k+3)=(2k-1).2(k+2)-2.(k-1).(2k+3)
=2[(2k-1).(k+2)-(k-1).(2k+3)] chia hết cho 2
=> N là số chắn (2)
Từ (1) và (2) suy ra điều phải chứng minh
\(N=\left(a-2\right).\left(a+3\right)-\left(a-3\right).\left(a+2\right)\)
\(a\in Z\)nên \(a\)có 1 trong 2 dạng \(2k\)và \(2k+1\)
\(TH1:a=2k\)
\(\Rightarrow N=\left(2k-2\right).\left(2k-3\right)-\left(2k-3\right).\left(2k+2\right)\)
\(+\)Vì \(2k-2\)là số chẵn nên \(\left(2k-2\right).\left(2k+3\right)\)chẵn
\(+\)Vì \(2k+2\)là số chẵn nên\(\left(2k-3\right).\left(2k+2\right)\)chẵn
\(\Rightarrow N\)là số chẵn.
\(TH2:a=2k+1\)
\(\Rightarrow N=\left(2k+1-2\right).\left(2k+1+3\right)-\left(2k+1-3\right).\left(2k+1+2\right)\)
\(\Rightarrow N=\left(2k-1\right).\left(2k+4\right)-\left(2k-2\right).\left(2k+3\right)\)
\(+\)Vì \(2k+4\)chẵn nên \(\left(2k-1\right).\left(2k+4\right)\)chẵn
\(+\)Vì \(\left(2k-2\right)\)chẵn nên\(\left(2k-2\right).\left(2k-3\right)\)chẵn
\(\Rightarrow N\)là số chẵn.
Từ TH1 và TH2:
\(\Rightarrow N\)là số chẵn.
\(N=(a-2)(a+3)-(a-3)(a+2)\)
\(=a(a-2)+3(a-2)-a(a-3)-2(a-3)\)
\(=a^2-2a+3a-6-a^2+3a-2a+6\)
\(=a^2+a-6-a^2+a+6\)
\(=(a^2-a^2)+a+a+(-6+6)\)
\(=2a\)là số chẵn với mọi a thuộc Z
Cho Trung bình cộng là 92,5. Tính hiệu của phép tính đó biết số lớn là 98 và số bé là 77.
Toán Nâng Siêu Cao lớp 1
Đây ko phải toán lớp 1
(98+77): 2= 87,5 nhé
tổng 2 số đầu là :
92.5x2=185
tổng 2 số sau là:
98+77=175
hiệu là:
185-175=10
Đ/s:10
Cần tìm gấp những bài tìm X LỚP 5 thật khó,siêu khó,nâng cao cho học sinh siêu giỏi
Bài 51: Cho hai hình vuông ABCD và MNPQ như trong hình vẽ. Biết BD = 12 cm. Hãy tính diện tích phần gạch chéo.
Bài 52: Bạn Toàn nhân một số với 2002 nhưng “đãng trí” quên viết 2 chữ số 0 của số 2002 nên kết quả “bị” giảm đi 3965940 đơn vị. Toàn đã định nhân số nào với 2002?
Bài 53: Người ta cộng 5 số và chia cho 5 thì được 138. Nếu xếp các số theo thứ tự lớn dần thì cộng 3 số đầu tiên và chia cho 3 sẽ được 127, cộng 3 số cuối và chia cho 3 sẽ được 148. Bạn có biết số đứng giữa theo thứ tự trên là số nào không?
Bài 54: Cho bảng ô vuông gồm 10 dòng và 10 cột. Hai bạn Tín và Nhi tô màu các ô, mỗi ô một màu trong 3 màu: xanh, đỏ, tím. Bạn Tín bảo: "Lần nào tô xong hết các ô cũng có 2 dòng mà trên 2 dòng đó có một màu tô số ô dòng này bằng tô số ô dòng kia". Bạn Nhi bảo: "Tớ phát hiện ra bao giờ cũng có 2 cột được tô như thế".
Nào, bạn hãy cho biết ai đúng, ai sai?
Bài 55: Tìm 4 số tự nhiên có tổng bằng 2003. Biết rằng nếu xóa bỏ chữ số hàng đơn vị của số thứ nhất ta được số thứ hai. Nếu xóa bỏ chữ số hàng đơn vị của số thứ hai ta được số thứ ba. Nếu xóa bỏ chữ số hàng đơn vị của số thứ ba ta được số thứ tư.
Bài 56: Một người mang ra chợ 5 giỏ táo gồm hai loại. Số táo trong mỗi giỏ lần lượt là: 20 ; 25 ; 30 ; 35 và 40. Mỗi giỏ chỉ đựng một loại táo. Sau khi bán hết một giỏ táo nào đó, người ấy thấy rằng : Số táo loại 2 còn lại đúng bằng nửa số táo loại 1. Hỏi số táo loại 2 còn lại là bao nhiêu?
Bạn nào cho mình một số bài nâng cao toán 6, nâng cao vừa vừa thôi. Cách làm luôn thì tốt
Bài 1: Tìm ƯC(2n + 1, 3n + 1).
Bài 2: Tìm ƯCLN(9n + 4; 2n - 1).
Bài 3: Cho a + 5b : 7(a,b €N). CMR: 10a + b : 7, điều ngược lại có đúng không?
Bài 4: Tìm số tự nhiên a biết rằng 398 : 9 thì dư 38 còn còn 450 chia cho a thì dư 18
Bài 5: Tìm hai số tự nhiên biết rằng tổng của chúng là 288 và ƯCLN của chúng là 24.
Bài 6: Tìm hai số tự nhiên biết rằng tổng của chúng là 192 và ƯCLN của chúng là 18.
Bài 7: Tìm hai số tự nhiên nhỏ hơn 56 và biết hiệu của chúng là 28 và ƯCLN của chúng là 14.
Bài 8: Giả sử hai số tự nhiên có hiệu là 84, ƯCLN của chúng là 12. Tìm hai số đó?
Bài 9: Cho hai số tự nhiên nhỏ hơn 200. Biết hiệu của chúng là 90 và ƯCLN là 15. Tìm hai số đó.
Bài 10: Tìm hai số tự nhiên biết rằng tích của chúng là 180 và ƯCLN của chúng là 3
Bài 11: Tìm hai số tự nhiên biết rằng tích của chúng là 8748 và ƯCLN của chúng là 27.
Bài 12: ƯCLN của hai số là 45 số lớn là 270 Tìm số nhỏ
Bài 13: ƯCLN của hai số là 4 số lớn là 8 Tìm số lớn
Bài 14: Tìm hai số tự nhiên a, b biết rằng BCNN(a,b) = 300 và ƯCLN(a,b) = 15.
Bài 15: Tìm hai số tự nhiên a, b biết rằng BCNN(a,b) = 72 và ƯCLN(a,b) = 12.
Bài 16: Tìm hai số tự nhiên biết rằng tích của chúng là 2940 và BCNN của chúng là 210.
Bài 17: Tìm hai số tự nhiên biết rằng tích của chúng là 2700 và BCNN của chúng là 900.
Bài 18: Tìm hai số tự nhiên a, b sao cho Tổng của ƯCLN và BCNN là 15.
Bài 19: Tìm hai số tự nhiên a, b sao cho Tổng của ƯCLN và BCNN là 55.
Bài 20: Tìm hai số tự nhiên a, b sao cho hiệu của BCNN và ƯCLN là 5.
Bài 21: Tìm ƯCLN(7n +3, 8n - 1) với (n €N*). Khi nào thì hai số đó nguyên tố cùng nhau.
Bài 22: Cho (a,b) = 1. Chứng tỏ rằng: (8a + 3) và (5b + 1) là nguyên tố cùng nhau.
Bài 23: Tìm số n nhỏ nhất để: n + 1; n + 3; n + 7 đều là nguyên tố.
Bài 24: Biết (a,b) = 95. Tìm (a + b, a - b).
Bài 25: Tìm n để 9n + 24 và 3n + 4 là hai số nguyên tố cùng nhau (n €N).
Bài 26: Tìm n để: 18n + 3 và 21n + 7 là hai số nguyên tố cùng nhau.
Bài 27: Tìm số tự nhiên nhỏ nhất khi chia cho 5 thì dư 1 còn chia cho 7 thì dư 5.
Bài 28: Tìm số tự nhiên n để các số sau nguyên tố cùng nhau:
a. 4n + 3 và 2n + 3
b. 7n + 13 và 2n + 4
c. 9n + 24 và 3n + 4
d. 18n + 3 và 21n + 7
Bài 29: Cho (a, b) = 1. Tìm:
a. (a + b, a - b);
b. (7a + 9b, 3a + 8b)
Bài 30: Tìm các giá trị a, b thuộc số tự nhiên sao cho:
a. [a, b] + (a, b) = 55
b. [a, b] – (a, b) = 5
c. [a, b] – (a, b) = 35
d. a + b = 30, [a, b] = 6.(a, b).
Bài 31: Số tự nhiên n có 54 ước. Chứng minh rằng tích các ước của n bằng n27.
Bài 32: Số tự nhiên n có 39 ước. Chứng minh rằng:
a. n là bình phương của một số tự nhiên a.
b. Tích các ước của n bằng a39.
Bài 33: Chứng minh rằng tích của ba số chẵn liên tiếp thì chia hết cho 48.
Bài 34: Chứng minh rằng tích của bốn số tự nhiên liên tiếp thì chia hết cho 24.
Bài 35: Cho một số tự nhiên chia hết cho 37 có ba chữ số. Chứng minh rằng bằng cách hoán vị vòng quanh các chữ số, ta được hai số nữa cũng chia hết cho 37.
Bài 36: Chứng minh rằng: (a, b) = (a + b, [a, b]).
Bài 37: Cho số ![]() chia hết cho 37. Chứng minh rằng:
chia hết cho 37. Chứng minh rằng:
a. Các số thu được bằng các hoán vị vòng quanh các chữ số của số đã cho cũng chia hết cho 37.
b. Nếu đổi chỗ a và d, ta vẫn được một số chia hết cho 37. Còn có thể đổi hai chữ số nào cho nhau mà vẫn được một số chia hết cho 37?
knha
Toán nâng cao !!

\(A=\dfrac{x+15}{x-2}=\dfrac{x-2+17}{x-2}\) \(\left(ĐK:x\ne2\right)\)
\(=\dfrac{x-2}{x-2}+\dfrac{17}{x-2}=1+\dfrac{17}{x-2}\)
Để \(A=1+\dfrac{17}{x-2}\in Z\)
thì \(\dfrac{17}{x-2}\in Z\)
\(\Rightarrow17⋮x-2\)
\(\Rightarrow x-2\inƯ\left(17\right)\)
\(\Rightarrow x-2\in\left\{1;17;-1;-17\right\}\)
\(\Rightarrow x\in\left\{3;19;1;-15\right\}\left(tm\right)\)
\(Vậy:x\in\left\{3;19;1;-15\right\}\)
Ta có:
x + 15 = x - 2 + 17
Để A ∈ Z thì (x + 15) ⋮ (x - 2)
⇒ 17 ⋮ (x - 2)
⇒ x - 2 ∈ Ư(17) = {-17; -1; 1; 17}
⇒ x ∈ {-15; 1; 3; 19}
Toán nâng cao !!
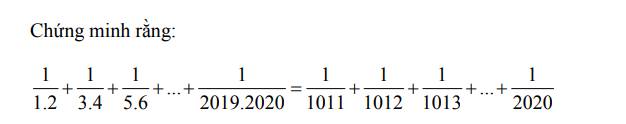
\(\dfrac{1}{1.2}+\dfrac{1}{3.4}+\dfrac{1}{5.6}+...+\dfrac{1}{2019.2020}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}-\dfrac{1}{6}+...+\dfrac{1}{2019}-\dfrac{1}{2020}\)
\(=\left(1+\dfrac{1}{3}+\dfrac{1}{5}+...+\dfrac{1}{2019}\right)-\left(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{6}+...+\dfrac{1}{2020}\right)\)
\(=\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2019}+\dfrac{1}{2020}\right)-2\left(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{6}+...+\dfrac{1}{2020}\right)\)
\(=\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2019}+\dfrac{1}{2020}\right)-\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{1010}\right)\)
\(=\dfrac{1}{1011}+\dfrac{1}{1012}+\dfrac{1}{1013}+...+\dfrac{1}{2020}\)
\(\Rightarrow dpcm\)
Toán nâng cao:

Ta có:
\(B=\dfrac{2008}{1}+\dfrac{2007}{2}+\dfrac{2006}{3}+...+\dfrac{2}{2007}+\dfrac{1}{2008}\)
\(B=2008+\dfrac{2007}{2}+\dfrac{2006}{3}+...+\dfrac{1}{2008}\)
\(B=1+\left(\dfrac{2007}{2}+1\right)+\left(\dfrac{2006}{3}+1\right)+...+\left(\dfrac{2}{2007}+1\right)+\left(\dfrac{1}{2008}+1\right)\)
\(B=1+\dfrac{2009}{2}+\dfrac{2009}{3}+\dfrac{2009}{4}+...+\dfrac{2009}{2008}\)
\(B=2009\cdot\left(\dfrac{1}{2}+\dfrac{1}{3}+....+\dfrac{1}{2009}\right)\)
\(\Rightarrow\dfrac{A}{B}=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2009}}{2009\cdot\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2009}\right)}\)
\(\Rightarrow\dfrac{A}{B}=\dfrac{1}{2009}\)