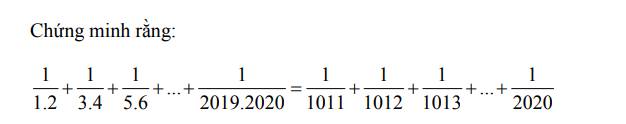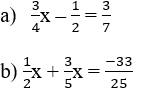\(\dfrac{1}{1.2}+\dfrac{1}{3.4}+\dfrac{1}{5.6}+...+\dfrac{1}{2019.2020}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}-\dfrac{1}{6}+...+\dfrac{1}{2019}-\dfrac{1}{2020}\)
\(=\left(1+\dfrac{1}{3}+\dfrac{1}{5}+...+\dfrac{1}{2019}\right)-\left(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{6}+...+\dfrac{1}{2020}\right)\)
\(=\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2019}+\dfrac{1}{2020}\right)-2\left(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{6}+...+\dfrac{1}{2020}\right)\)
\(=\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2019}+\dfrac{1}{2020}\right)-\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{1010}\right)\)
\(=\dfrac{1}{1011}+\dfrac{1}{1012}+\dfrac{1}{1013}+...+\dfrac{1}{2020}\)
\(\Rightarrow dpcm\)