Chủ đề / Chương

Bài học

Hãy tham gia nhóm Học sinh Hoc24OLM
Bạn chưa đăng nhập. Vui lòng đăng nhập để hỏi bài
Pham Trong Bach
Tìm góc giữa 2 đường thẳng d: 6x- 5y+ 15 0 và ∆ 2 :   x 10 - 6 t y...
Đọc tiếp
Lớp 10 Toán
Những câu hỏi liên quan
Pham Trong Bach
Tìm côsin góc giữa 2 đường thẳng d1: 10x+ 5y- 10 và  d 2 :   x   2 +   t   y  ...
Đọc tiếp
Xem chi tiết
Lớp 10 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
22 tháng 12 2017 lúc 18:16

Lời giải

Chọn C

Vectơ pháp tuyến của d1; d2 lần lượt là  n 1 → ( 2 ; 1   )   ;   n 2 → ( 1 ; 1 )

Cos( d1; d2) =

Bình luận (0)
Tú Ngô

Cho d1:2x+5y+4=0 và d2:5x-2y+6=0.Số đo của góc giữa 2 đường thẳng d1 và d2 là? A.90° B.60° C.45° D.30°

Xem chi tiết
Lớp 10 Toán

Khách
 
Nguyễn Lê Phước Thịnh
Nguyễn Lê Phước Thịnh CTV
8 tháng 3 2022 lúc 22:22

Chọn A

Bình luận (0)
Tạ Tuấn Anh
Tạ Tuấn Anh
8 tháng 3 2022 lúc 22:23

A

Bình luận (1)
Phạm Quang Huy
Phạm Quang Huy
8 tháng 3 2022 lúc 22:24

A

Bình luận (0)
Xem thêm câu trả lời
Nguyễn Quốc Cường

Cho đường tròn C x^2 + y² + 2x + 5y - 15 = 0 Viết phương trình đường thẳng vuông góc với đường thẳng delta: 4x + 3y - 2 = 0 cắt đường tròn C tại hai điểm a và b sao cho ab=6

Xem chi tiết
Lớp 10 Toán Chương 2: HÀM SỐ BẬC NHẤT VÀ BẬC HAI

Khách
 
Nguyễn Lê Phước Thịnh
Nguyễn Lê Phước Thịnh CTV
28 tháng 4 2023 lúc 22:46

loading...

Bình luận (0)
Nguyễn Quốc Cường

Cho đường tròn C x^2 + y² + 2x + 5y - 15 = 0 Viết phương trình đường thẳng vuông góc với đường thẳng delta: 4x + 3y - 2 = 0 cắt đường tròn C tại hai điểm a và b sao cho ab=6 Giúp với mọi người ơiii SOS

Xem chi tiết
Lớp 10 Toán II. ĐƯỜNG TRÒN

Khách
 
Nguyễn Lê Phước Thịnh
Nguyễn Lê Phước Thịnh CTV
28 tháng 4 2023 lúc 22:25

Sửa đề: x^2+y^2+2x+6y-15=0

Δ vuông góc d nên Δ: 3x+4y+c=0

(C);x^2+y^2+2x+6y-15=0

=>x^2+2x+1+y^2+6y+9-25=0

=>(x+1)^2+(y+3)^2=25

=>R=5; I(-1;-3)

Kẻ IH vuông góc AB

=>H là trung điểm của AB

=>AH=6/2=3cm

=>IH=4cm

=>d(I;Δ)=IH=4

=>|c+3-12|/5=4

=>c=-11 hoặc c=29

=>3x+4y-11=0 hoặc 3x+4y+29=0

Bình luận (0)
xữ nữ của tôi

1: Khoảng cách giữa 2 đường thẳng d: 3x-4y=0 và d' : 6x-8y -101=0

2: Cho đường thẳng d: 7x+10y-15=0 . Trong các điểm M(1;3) , N( 0;4) , P( 8;0) ,Q(1;5) . Điểm nào cách xa d nhất

Xem chi tiết
Lớp 10 Toán §1. Phương trình đường thẳng

Khách
 
Nguyễn Lê Phước Thịnh
Nguyễn Lê Phước Thịnh CTV
24 tháng 5 2022 lúc 13:59

Bài 2:

\(d_M=\dfrac{\left|7\cdot1+10\cdot3-15\right|}{\sqrt{7^2+10^2}}=\dfrac{22}{\sqrt{149}}\)

\(d_N=\dfrac{\left|7\cdot0+10\cdot4-15\right|}{\sqrt{7^2+10^2}}=\dfrac{25}{\sqrt{149}}\)

\(d_P=\dfrac{\left|8\cdot7+0\cdot10-15\right|}{\sqrt{7^2+10^2}}=\dfrac{41}{\sqrt{149}}\)

\(d_Q=\dfrac{\left|7\cdot1+10\cdot5-15\right|}{\sqrt{7^2+10^2}}=\dfrac{42}{\sqrt{149}}\)

Vì 22<25<41<42

nên \(d_M< d_N< d_P< d_Q\)

Do đó: Q cách xa d nhất

Bình luận (0)
Pham Trong Bach

Cho bốn điểm A(1; 0; 0), B(0; 1; 0), C(0; 0; 1), D(-2; 1; -1) Tìm góc giữa hai đường thẳng AB và CD

Xem chi tiết
Lớp 12 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
27 tháng 11 2017 lúc 10:37

Giải bài 1 trang 91 sgk Hình học 12 | Để học tốt Toán 12

Bình luận (0)
Pham Trong Bach
Cho mặt phẳng α : 3x+5y-z-20 và đường thẳng d :   x 12 + 4 t y 9 + 3 t...
Đọc tiếp
Xem chi tiết
Lớp 12 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
7 tháng 10 2019 lúc 13:48

Bình luận (0)
Pham Trong Bach
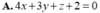
Cho mặt phẳng (α) có phương trình: 3x + 5y - z - 2 0 và đường thẳng d có phương trình:  x 12 + 4 t y 9 + 3 t z...
Đọc tiếp
Xem chi tiết
Lớp 12 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
21 tháng 2 2017 lúc 3:01

(β) vuông góc với d

⇒ (β) nhận vtcp của d 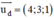Giải bài 6 trang 92 sgk Hình học 12 | Để học tốt Toán 12 là 1 vtpt.

(β) đi qua M(0; 0; -2)

⇒ (β): 4x + 3y + z + 2 = 0.

Bình luận (0)
Pham Trong Bach
Cho mặt phẳng ( α ) : 3 x + 5 y - z - 2 0  và đường thẳng d : x 12 + 4 t y 9 + 3...
Đọc tiếp
Xem chi tiết
Lớp 0 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
4 tháng 11 2017 lúc 3:01

Chọn A

Tìm tọa độ giao điểm M bằng cách giải hệ. Mặt phẳng (P) cần tìm qua điểm M và nhận vecto chỉ phương của d làm vecto pháp tuyến.

Bình luận (0)

Khoá học trên OLM (olm.vn)