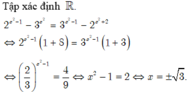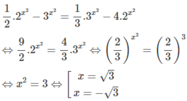Giải phương trình: 2x2 – 8x = -1

Những câu hỏi liên quan
Giải phương trình: 2 x 2 – 8 x = - 1
2 x 2 − 8 x = − 1 ⇔ x 2 − 4 x = ( − 1 ) / 2 ⇔ x 2 − 4 x + 4 = ( − 1 ) / 2 + 4 ⇔ ( x − 2 ) 2 = 7 / 2 ⇔ x − 2 = ± ( 7 / 2 ) ⇔ x = 2 ± ( 7 / 2 )
Vậy phương trình có hai nghiệm:
x 1 = 2 + √ ( 7 / 2 ) ; x 2 = 2 - √ ( 7 / 2 )
Đúng 0
Bình luận (0)
Giải phương trình :
1) √x2+x+2 + 1/x= 13-7x/2
2) x2 + 3x = √1-x + 1/4
3) ( x+3)√48-x2-8x= 28-x/ x+3
4) √-x2-2x +48= 28-x/x+3
5) 3x2 + 2(x-1)√2x2-3x +1= 5x + 2
6) 4x2 +(8x - 4)√x -1 = 3x+2√2x2 +5x-3
7) x3/ √16-x2 + x2 -16 = 0
Giải các phương trình sau:
2
x
2
-
1
-
3
x
2
3
x
2
-
1
-
2
x
2
+
2
. Tổng các nghiệm của phương trình là: A. 2 B. 3 C....
Đọc tiếp
Giải các phương trình sau: 2 x 2 - 1 - 3 x 2 = 3 x 2 - 1 - 2 x 2 + 2 . Tổng các nghiệm của phương trình là:
A. 2
B. 3
C. 0
D. 2 3
Hãy cho biết phương trình nào trong các phương trình sau đây là phương trình đường tròn:
2x2 + y2 – 8x + 2y – 1 = 0;
x2 + y2 + 2x – 4y – 4 = 0;
x2 + y2 – 2x – 6y + 20 = 0;
x2 + y2 + 6x + 2y + 10 = 0.
+ 2x2 + y2 – 8x + 2y – 1 = 0 không phải phương trình đường tròn vì hệ số của x2 khác hệ số của y2.
+ Phương trình x2 + y2 + 2x – 4y – 4 = 0 có :
a = –1; b = 2; c = –4 ⇒ a2 + b2 – c = 9 > 0
⇒ phương trình trên là phương trình đường tròn.
+ Phương trình x2 + y2 – 2x – 6y + 20 = 0 có :
a = 1; b = 3; c = 20 ⇒ a2 + b2 – c = –10 < 0
⇒ phương trình trên không là phương trình đường tròn.
+ Phương trình x2 + y2 + 6x + 2y + 10 = 0 có :
a = –3; b = –1; c = 10 ⇒ a2 + b2 – c = 0 = 0
⇒ phương trình trên không là phương trình đường tròn.
Đúng 0
Bình luận (0)
Giải các phương trình sau:
2
x
2
-
1
-
3
x
2
3
x
2
-
1
-
2
x
2...
Đọc tiếp
Giải các phương trình sau: 2 x 2 - 1 - 3 x 2 = 3 x 2 - 1 - 2 x 2 + 2
Giúp vs ạBài 1 giải các bất phương trình saua.x2 - x - 6 0b.2x2 - 7x + 5 0c.3x2 - 9x + 6 ≥ 0d.2x2 - 5x + 3 0Bài 2 Giải phương trình sauA.√x2 + x + 5 √2x2 - 4x + 1B.√11x2 -14x - 12 √3x2 + 4x - 7
Đọc tiếp
Giúp vs ạ
Bài 1 giải các bất phương trình sau
a.x2 - x - 6 = 0
b.2x2 - 7x + 5 < 0
c.3x2 - 9x + 6 ≥ 0
d.2x2 - 5x + 3 < 0
Bài 2 Giải phương trình sau
A.√x2 + x + 5 = √2x2 - 4x + 1
B.√11x2 -14x - 12 = √3x2 + 4x - 7
Bài 2:
a: =>2x^2-4x+1=x^2+x+5
=>x^2-5x-4=0
=>\(x=\dfrac{5\pm\sqrt{41}}{2}\)
b: =>11x^2-14x-12=3x^2+4x-7
=>8x^2-18x-5=0
=>x=5/2 hoặc x=-1/4
Đúng 0
Bình luận (0)
Cho phương trình sau , nhận xét nào sau đây đúng ?
2
x
2
-
8
x
-
3
x
2
-
4
x
-
5
12
A. Phương trình có hai nghiệm
x
1
,
x
2
thỏa mãn ...
Đọc tiếp
Cho phương trình sau , nhận xét nào sau đây đúng ?
2 x 2 - 8 x - 3 x 2 - 4 x - 5 = 12
A. Phương trình có hai nghiệm x 1 , x 2 thỏa mãn x 1 + x 2 = 5
B. Phương trình có hai nghiệm x 1 , x 2 thỏa mãn x 1 . x 2 = -9
C. Nghiệm của phương trình đã cho thỏa mãn x ∈ [-1; 5]
D. Phương trình có hai nghiệm x 1 , x 2 thỏa mãn x 1 - 9 / x 2 = 4
Chọn đáp án B.
Điều kiện:
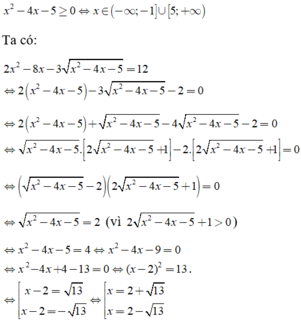
Kết hợp điều kiện ta thấy hai giá trị trên đều thỏa mãn điều kiện.
Khi đó ta có 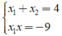
Đúng 0
Bình luận (0)
Giải phương trình bằng cách đặt ẩn phụ:
2 x 2 - 2 x 2 + 3 x 2 - 2 x + 1 = 0
2(x2 – 2x)2 + 3(x2 – 2x) + 1 = 0 (1)
Đặt x2 – 2x = t,
(1) trở thành : 2t2 + 3t + 1 = 0 (2).
Giải (2) :
Có a = 2 ; b = 3 ; c = 1
⇒ a – b + c = 0
⇒ (2) có nghiệm t1 = -1; t2 = -c/a = -1/2.
+ Với t = -1 ⇒ x2 – 2x = -1 ⇔ x2 – 2x + 1 = 0 ⇔ (x – 1)2 = 0 ⇔ x = 1.
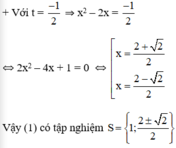
Đúng 0
Bình luận (0)
Giải phương trình trùng phương: 2 x 2 + 1 = 1 x 2 - 4
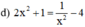
Điều kiện xác định: x ≠ 0.
Quy đồng, khử mẫu ta được :
2x4 + x2 = 1 – 4x2
⇔ 2x4 + x2 + 4x2 – 1 = 0
⇔ 2x4 + 5x2 – 1 = 0 (1)
Đặt t = x2, điều kiện t > 0.
Khi đó (1) trở thành : 2t2 + 5t – 1 = 0 (2)
Giải (2) :
Có a = 2 ; b = 5 ; c = -1
⇒ Δ = 52 – 4.2.(-1) = 33 > 0
⇒ Phương trình có hai nghiệm phân biệt:
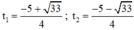
Đối chiếu với điều kiện thấy có nghiệm t1 thỏa mãn.
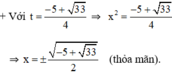
Vậy phương trình có tập nghiệm 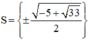
Đúng 0
Bình luận (0)