Với giá trị nào của m thì hàm số y = tan x - 2 m tan x - 2 đồng biến trên khoảng 0 ; π 4 ?
A. 1 < m ≤ 2
B. - ∞ ; 2
C. 1 < m < 2
D. 2 ; + ∞
Với giá trị nào của x thì giá trị của các hàm số y = tan(π/4 - x) và y = tan 2x bằng nhau?
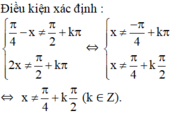
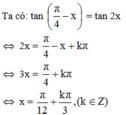
Kết hợp với điều kiện xác định suy ra
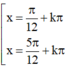 (k ∈ Z)
(k ∈ Z)
Vậy với 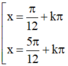 (k ∈ Z)
(k ∈ Z)
thì 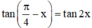
cho hàm số: y = (m-2)x + m+1 (1)
a) với giá trị nào của m thì hs (1) là hàm số bậc nhất
b) với giá trị nào của m thì hs (1) đồng biến
c) vẽ đồ thị hàm số m =1
d) với giá trị nào của m thì đồ thị hàm số (1) đi qua A(2;1)
e) với giá trị nào của m thì đồ thị hàm số (1) song song với y = 3x+2
f) với giá trị nào của m thì đồ thị hàm số (1) tạo với trục Ox một góc tù?
g) với giá trị nào của m thì đồ thị hàm số (1) cắt đường thẳng y = 5x+6 tại trục tung
h) với m =3 tính góc tạo thành bởi đồ thị hàm số với trục hoành và tính khoảng cách từ gốc tọa độ đến đường thẳng
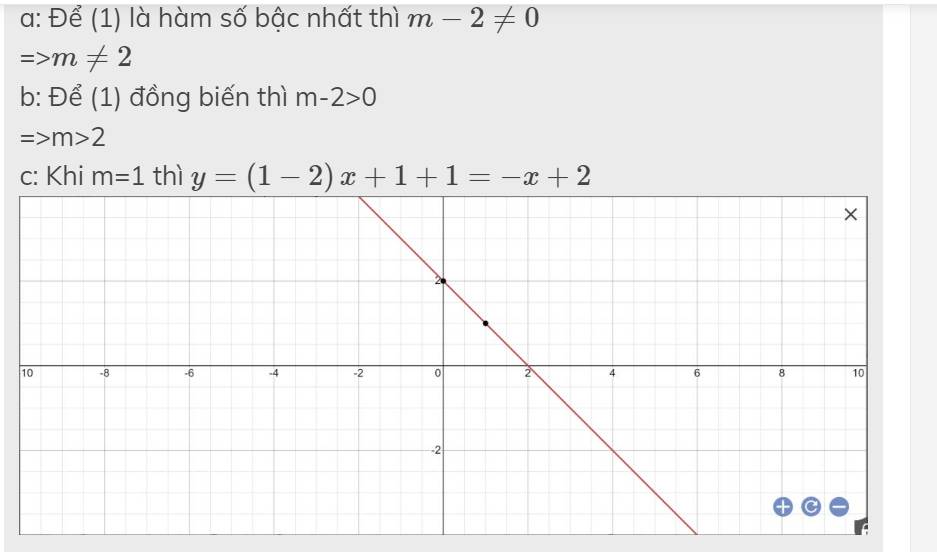


h: Khi m=3 thì \(y=\left(3-2\right)x+3+1=x+4\)
Gọi \(\alpha\) là góc tạo bởi đồ thị hàm số y=x+4 với trục Ox
\(tan\alpha=a=1\)
=>\(\alpha=45^0\)
y=x+4
=>x-y+4=0
Khoảng cách từ O(0;0) đến đường thẳng x-y+4=0 là:
\(\dfrac{\left|0\cdot1+0\cdot\left(-1\right)+4\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{4}{\sqrt{2}}=2\sqrt{2}\)
cho hàm số: y = (m-2)x + m+1 (1)
a) với giá trị nào của m thì hs (1) là hàm số bậc nhất
b) với giá trị nào của m thì hs (1) đồng biến
c) vẽ đồ thị hàm số m =1
d) với giá trị nào của m thì đồ thị hàm số (1) đi qua A(2;1)
e) với giá trị nào của m thì đồ thị hàm số (1) song song với y = 3x+2
f) với giá trị nào của m thì đồ thị hàm số (1) tạo với trục Ox một góc tù?
g) với giá trị nào của m thì đồ thị hàm số (1) cắt đường thẳng y = 5x+6 tại trục tung
h) với m =3 tính góc tạo thành bởi đồ thị hàm số với trục hoành và tính khoảng cách từ gốc tọa độ đến đường thẳng
a: Để (1) là hàm số bậc nhất thì \(m-2\ne0\)
=>\(m\ne2\)
b: Để (1) đồng biến thì m-2>0
=>m>2
c: Khi m=1 thì \(y=\left(1-2\right)x+1+1=-x+2\)
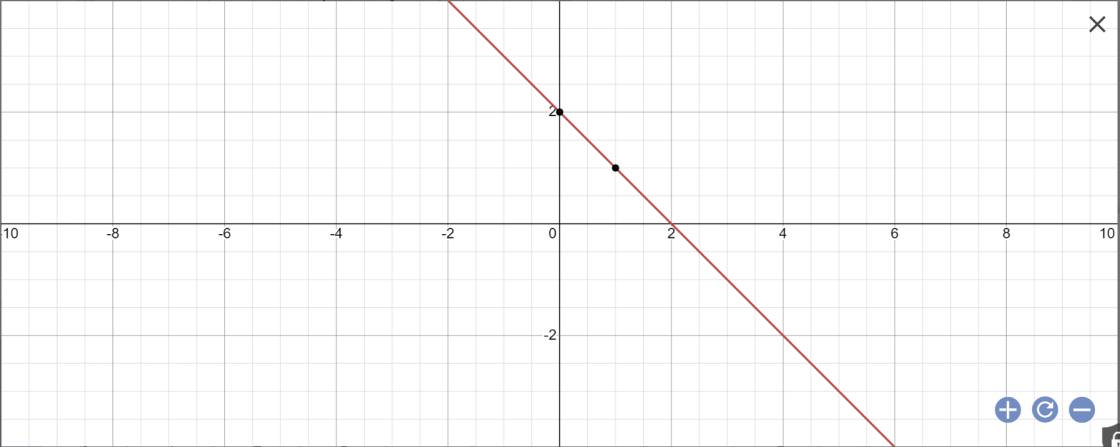
d: Thay x=2 và y=1 vào (1), ta được:
\(2\left(m-2\right)+m+1=1\)
=>2m-4+m=0
=>3m-4=0
=>3m=4
=>\(m=\dfrac{4}{3}\)
e: Để (1)//y=3x+2 thì \(\left\{{}\begin{matrix}m-2=3\\m+1< >2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=3\\m< >1\end{matrix}\right.\)
=>m=3
f: Để (1) tạo với trục Ox một góc tù thì m-2<0
=>m<2
g: Thay x=0 vào y=5x+6, ta được:
\(y=5\cdot0+6=6\)
Thay x=0 và y=6 vào (1), ta được:
\(0\left(m-2\right)+m+1=6\)
=>m+1=6
=>m=5
Với giá trị nào của m thì hàm số sau đây là hàm số bậc nhất
a, y=\(\sqrt{m-3}\times x+\dfrac{2}{3}\)
b, y= \(\dfrac{\sqrt{m}+\sqrt{5}}{\sqrt{m}-\sqrt{5}}\times x+2010\)
với giá trị nào của m thì hàm số ở ý a là hàm số đồng biến. Với gtri nào của m thì hàm số ở ý b là hàm nghịch biến
a) Ta có: \(y=\sqrt{m-3}\cdot x+\dfrac{2}{3}\left(m\ge3\right)\)
Để đây là hàm số bậc nhất thì: \(\sqrt{m-3}\ne0\Leftrightarrow m=3\)
Do: \(\sqrt{m-3}\ge0\forall m\ge3\)
Nên với \(m\ge3\) thì y đồng biến trên R
b) Ta có: \(y=\dfrac{\sqrt{m}+\sqrt{5}}{\sqrt{m}-\sqrt{5}}\cdot x+2010\left(m\ge0;m\ne5\right)\)
Để đây là hàm số bậc nhất thì: \(\sqrt{m}-\sqrt{5}\ne0\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\m\ne5\end{matrix}\right.\)
Do \(\sqrt{m}+\sqrt{5}>0\Rightarrow\sqrt{m}-\sqrt{5}< 0\Leftrightarrow m< 5\)
Vậy với 0 ≤ m < 5 thì y nghịch biến trên R
a) Để hàm số là hàm số bậc nhất thì:
√(m - 3) > 0
⇔ m - 3 > 0
⇔ m > 3
Vậy với m > 3 thì hàm số đã cho là hàm bậc nhất
b) Để hàm số là hàm bậc nhất thì √m - √5 ≠ 0 và m ≥ 0
⇔ √m ≠ √5
⇔ m ≠ 5
Vậy m ≠ 5 và m ≥ 0 thì hàm số đã cho làm hàm số bậc nhất
*) Để hàm số ở câu a là hàm đồng biến thì m > 3
*) Để hàm số ở câu b là hàm nghịch biến thì √m < √5
⇔ 0 \(\le\) m < 5
Vậy 0 \(\le\) m < 5 thì hàm số ở câu b là hàm số nghịch biến
cho 2 hàm số y=\(\dfrac{m-1}{m+1}\)x +m+2 (1)
a, với giá trị nào thì hàm số (1) là hàm số bậc nhất
b, với giá trị nào thì hàm số (1) là hàm số đồng biến
c, với giá trị nào của m thì đồ thị hàm số (1) đi qua điểm A(1;2)
\(a,\Leftrightarrow\dfrac{m-1}{m+1}\ne0\Leftrightarrow m\ne\pm1\\ b,\Leftrightarrow\dfrac{m-1}{m+1}>0\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\\ c,\Leftrightarrow\dfrac{m-1}{m+1}+m+2=2\\ \Leftrightarrow\dfrac{m-1+m^2+m}{m+1}=0\\ \Leftrightarrow m^2+2m-1=0\\ \Leftrightarrow\left[{}\begin{matrix}m=-1+\sqrt{2}\\m=-1-\sqrt{2}\end{matrix}\right.\)
a) với những giá trị nào của m thì hàm số y = (m + 6)x - 7 đồng biến?
b) với những giá trị nào của k thì hàm số y = (-k + 9)x + 100 nghịch biến?
c) với những giá trị nào của m thì đồ thị của hàm số y = 12x + (5 + m) và y = -3x + (3 - m) cắt nhau tại một điểm trên trục tung
a: Để hàm số y=(m+6)x-7 đồng biến thì m+6>0
=>m>-6
b: Để hàm số y=(-k+9)x+100 nghịch biến thì -k+9<0
=>-k<-9
=>k>9
c: Để hai đồ thị hàm số y=12x+(5+m) và y=-3x+(3-m) cắt nhau tại một điểm trên trục tung thì
\(\left\{{}\begin{matrix}m+5=3-m\\12\ne-3\left(đúng\right)\end{matrix}\right.\)
=>m+5=3-m
=>2m=-2
=>m=-1
Câu 3: cho hàm số y = ( m - 3 ) x a, Với giá trị nào của m thì hàm số đồng biến? Nghịch biến? b, Với giá trị nào của m thì hàm số đi qua A (1,2) C, Với giá trị nào của m thì hàm số đi qua B (1,2) D, Vẽ đô thị của 2 hàm số ứng với m vừa tìm đc ở câu a,b
a: Để hàm số đồng biến trên R thì m-3>0
=>m>3
Để hàm số nghịch biến trên R thì m-3<0
=>m<3
b: Thay x=1 và y=2 vào y=(m-3)x, ta được:
\(1\left(m-3\right)=2\)
=>m-3=2
=>m=5
c: Thay x=1 và y=2 vào y=(m-3)x, ta được:
m-3=2
=>m=5
d: Khi m=5 thì y=(5-3)x=2x
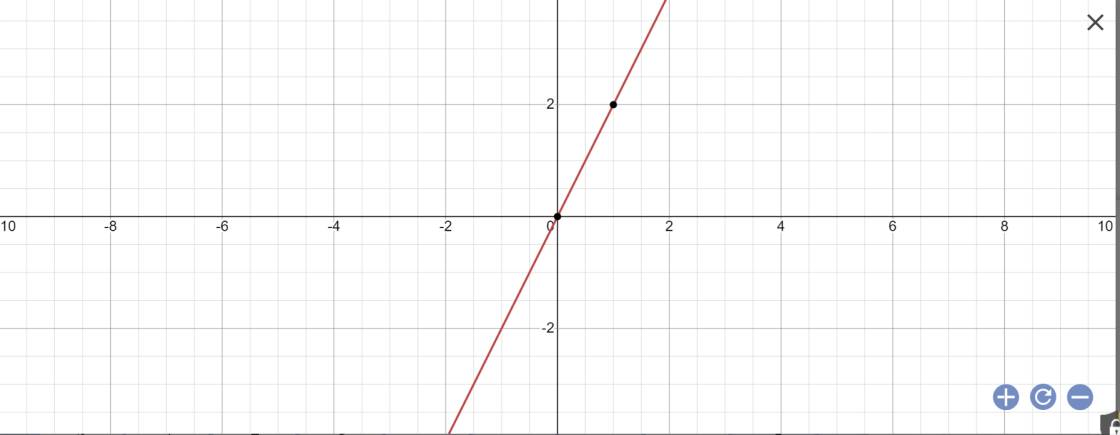
I.TỰ LUẬN
BÀI 1: a) Với giá trị nào của m thì hàm số y = (2m-1)x +5 là hàm số bậc nhất?
b) Với những giá trị nào của m thì hàm số bậc nhất y = (m – 1)x + 3 đồng biến?
c) Với những giá trị nào của k thì hàm số bậc nhất y = (5 – k)x + 1 nghịch biến?
Cho 2 hàm số bậc nhất y = (3m - 1)x + 2 và y = (m + 3)x +1
a) Với giá trị nào của m thì đồ thị của 2 hàm số là 2 đường thẳng song song với nhau?
b) Với giá trị nào của m thì đò thị của 2 hàm số là 2 đường thẳng cắt nhau?
\(a,\Leftrightarrow3m-1=m+3\Leftrightarrow2m=4\Leftrightarrow m=2\\ b,\Leftrightarrow3m-1\ne m+3\Leftrightarrow m\ne2\)
Cho hàm số bậc nhất y=(m-1/2)x+2
a, với giá trị nào của m để hàm số là hàm số bậc nhất? Xác định các hệ số a,b
b, cho hàm số bậc nhất y=(m-1/2)x+2. Với giá trị nào của m thì hàm số đồng biến,nghịch biến.
c, cho hàm số bậc nhất y=0.5x+2. Tính giá trị của y khi biết giá trị của x=2