Cho a, b, c là ba số thực dương, khác 1 và a b c ≠ 1 . Biết log a 3 = 2 , log b 3 = 1 4 và log a b c 3 = 2 15 . Khi đó, giá trị của log c 3 bằng bao nhiêu?
A. log c 3 = 1 3
B. log c 3 = 1 2
C. log c 3 = 3
D. log c 3 = 2
Những câu hỏi liên quan
SGK Cánh Diều
13 tháng 8 2023 lúc 21:41
Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số lôgarit \(y = {\log _a}x;\,y = {\log _b}x;\,y = {\log _c}x\) được cho bởi Hình 15. Kết luận nào sau đây là đúng với ba số a, b, c?
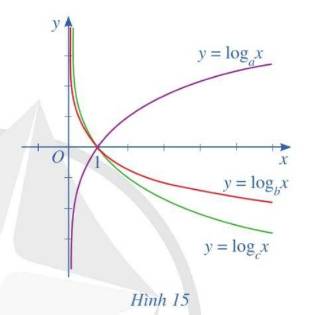
A. c < a < b
B. c < b < a
C. a < b < c
D. b < c < a
SGK Cánh Diều
13 tháng 8 2023 lúc 21:07
Hoạt động 5
Cho ba số thực dương a, b, c với \(a \ne 1\,;\,c \ne 1\)
a) Bằng cách sử dụng tính chất \(b = {a^{{{\log }_a}b}}\), chứng tỏ rằng \({\log _c}b = {\log _a}b.{\log _c}a\)
b) So sánh \({\log _a}b\,\,\,và \frac{{{{\log }_c}b}}{{{{\log }_c}a}}\)
a) \({\log _c}b = {\log _a}b.{\log _c}a \Leftrightarrow {a^{{{\log }_c}b}} = {a^{{{\log }_a}b.{{\log }_c}a}} \Leftrightarrow {c^{{{\log }_c}b}} = {\left( {{c^{{{\log }_c}a}}} \right)^{{{\log }_a}b}} \Leftrightarrow b = {a^{{{\log }_a}b}} \Leftrightarrow b = b\) (luôn đúng)
Vậy \({\log _c}b = {\log _a}b.{\log _c}a\)
b) Từ \({\log _c}b = {\log _a}b.{\log _c}a \Leftrightarrow {\log _a}b = \frac{{{{\log }_c}b}}{{{{\log }_c}a}}\)
Đúng 0
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
15 tháng 8 2023 lúc 19:52
Cho hai số thực dương a, b với \(a \ne 1\). Khẳng định nào sau đây là đúng?
A. \({\log _a}\left( {{a^3}{b^2}} \right) = 3 + {\log _a}b\).
B. \({\log _a}\left( {{a^3}{b^2}} \right) = 3 + 2{\log _a}b\).
C. \({\log _a}\left( {{a^3}{b^2}} \right) = \frac{3}{2} + {\log _a}b\).
D. \({\log _a}\left( {{a^3}{b^2}} \right) = \frac{1}{3} + \frac{1}{2}{\log _a}b\).
\(log_a\left(a^3b^2\right)=log_aa^3+log_ab^2=3+2\cdot log_ab\)
=>B
Đúng 0
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
15 tháng 8 2023 lúc 19:53
Cho bốn số thực dương a, b, x, y với \(a,b \ne 1\). Khẳng định nào sau đây là sai?
A. \({\log _a}(xy) = {\log _a}x + {\log _b}y\).
B. \({\log _a}\frac{x}{y} = {\log _a}x - {\log _a}y\).
C. \({\log _a}\frac{1}{x} = \frac{1}{{{{\log }_a}x}}\).
D. \({\log _a}b \cdot {\log _b}x = {\log _a}x\).
1) Cho a,b là các số thực dương khác 1 và thoả mãn ab khác 1. Rút gọn biểu thức sau: P=(logab + logba + 2)(logab - logabb).logba - 1
SGK Cánh Diều
13 tháng 8 2023 lúc 21:39
Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số mũ \(y = {a^x};\,y = {b^x};\,y = {c^x}\) được cho bởi Hình 14. Kết luận nào sau đây là đúng đối với ba số a, b, c ?
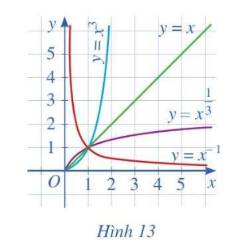
A. c < a < b
B. c < b < a
C. a < b < c
D. b < c < a
\(-\) Do \(c^x\) nghịch biến\(,a^x,b^x\) đồng biến\(\Rightarrow c< 1,a>1,b>1\Rightarrow c\) nhỏ nhất \(\Rightarrow\)Loại \(C,D\)
\(-\) Dựa vào đồ thị ta thấy\(,b^x\) có đồ thị đi lên cao hơn so với \(a^x\Rightarrow b>a\Rightarrow\) Chọn \(A\)
Đúng 1
Bình luận (0)
Cho a, b, c là các số thực dương khác 1. Biết
log
a
c
2
,
log
b
c
3.
Tính
P
l
o
g
c
a
b
A.
P
5
6
B.
P
1
C.
P...
Đọc tiếp
Cho a, b, c là các số thực dương khác 1.
Biết log a c = 2 , log b c = 3. Tính P = l o g c a b
A. P = 5 6
B. P = 1
C. P = 2 3
D. P = 1 2
Đáp án A
Ta có:
P = log c a b = log c a + log c b = 1 log a c + 1 log b c = 1 2 + 1 3 = 5 6 .
Đúng 0
Bình luận (0)
Giả sử a, b là các số thực sao cho x3 + y3 a.103x + b.102x đúng với mọi số thực dương x, y, z thỏa mãn log (x + y) z và log(x2 + y2) z + 1. Giá trị của a+b bằng: A.
-
31
2
B.
-
25
2
C.
31
2
D.
29
2
Đọc tiếp
Giả sử a, b là các số thực sao cho x3 + y3 = a.103x + b.102x đúng với mọi số thực dương x, y, z thỏa mãn log (x + y) = z và log(x2 + y2) = z + 1. Giá trị của a+b bằng:
A. - 31 2
B. - 25 2
C. 31 2
D. 29 2
Đáp án D.
Ta có
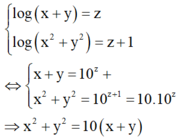
Khi đó
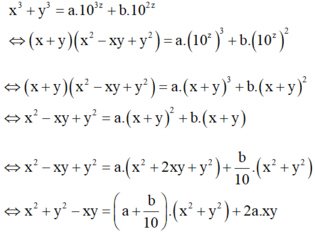
Đồng nhất hệ số, ta được
Đúng 0
Bình luận (0)
Cho các số thực dương a, b với a≠1 và log a b 0. Khẳng định nào sau đây là đúng? A.
0
a
,
b
1
0
a
1...
Đọc tiếp
Cho các số thực dương a, b với a≠1 và log a b >0. Khẳng định nào sau đây là đúng?
A. 0 < a , b < 1 0 < a < 1 < b
B. 0 < a , b < 1 1 < a , b
C. 0 < a , b < 1 0 < b < 1 < a
D. 0 < b < 1 < a 1 < a , b
