Gọi M, N là giao điểm của y = x+1 và y = 2 x + 4 x - 1 Khi đó hoành độ trung điểm của I của đoạn thẳng MN bằng
A. 2
B. 1
C. 0
D. -1
Những câu hỏi liên quan
a) Vẽ trên cùng một mặt phẳng toạ độ Oxy đồ thị các hàm số sau (d_{i}) / y = - 1/2 * x - 2(d_{2}) / y = 1/4 * x + 2 b) Gọi giao điểm của hai đường thăng (d) và (d2) với trục tung lần lượt là M và N ; giao điểm của (d)và (d) là P. Xác định toạ độ của M, N và P
a)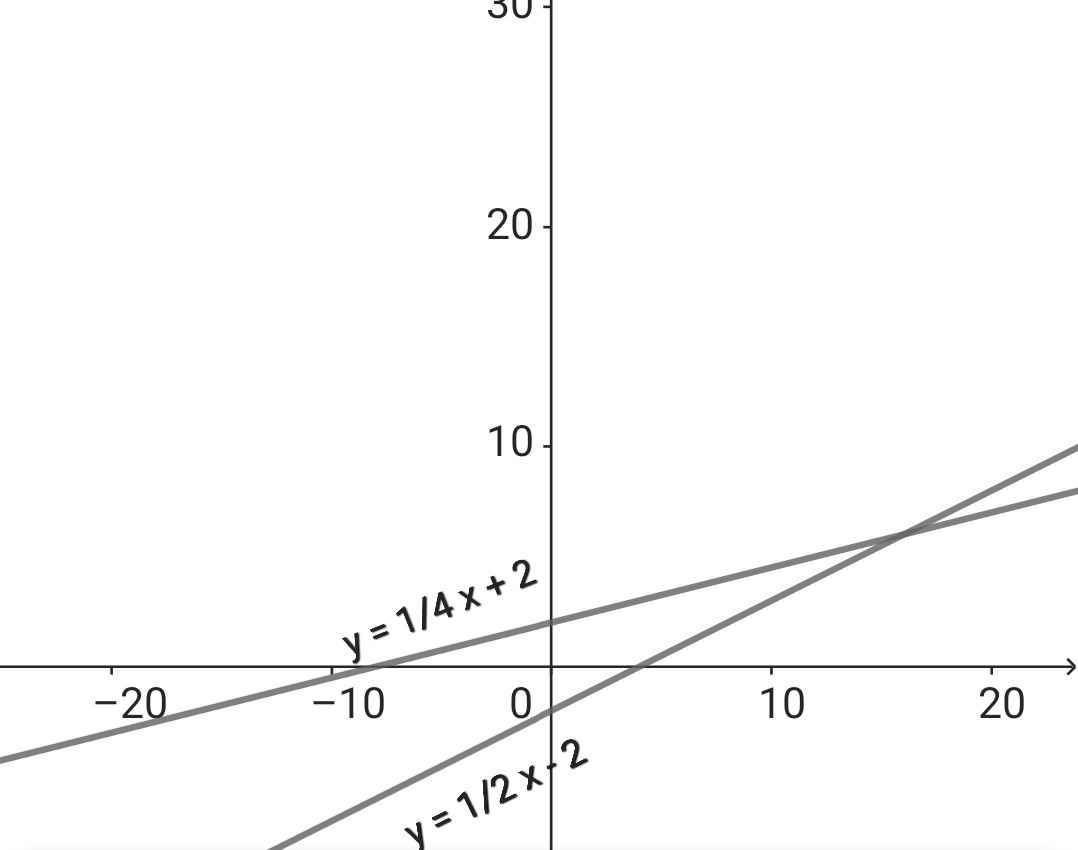 
b) *) Thay x = 0 vào (d) ta có:
y = 1/2 . 0 - 2 = -2
⇒ M(0; -2)
Thay x = 0 vào (d) ta có:
y = 1/4 . 0 + 2 = 2
⇒ N(0; 2)
Phương trình hoành độ giao điểm của (d) và (d)
1/2 x - 2 = 1/4 x + 2
⇔ 1/2 x - 1/4 x = 2 + 2
⇔ 1/4 x = 4
⇔ x = 4 : (1/4)
⇔ x = 16
Thay x = 16 vào (d) ta có:
y = 1/2 . 16 - 2 = 6
⇒ P(16; 6)
Đúng 2
Bình luận (0)
Cho một parabol y = a.x2. Gọi M , N là các giao điểm của đường thẳng y = x + 4 với parabol. Tìm toạ độ của M và N theo a
Gọi A là giao điểm của 2 đường thẳng y=-x+1 và y=x+3. Tìm số nguyên dương m để A thuộc đồ thị hàm số y = (m-1)x+m^2-1
Pt hoành độ giao điểm:
\(-x+1=x+3\Rightarrow2x=-2\)
\(\Rightarrow x=-1\Rightarrow y=x+3=2\)
\(\Rightarrow A\left(-1;2\right)\)
Để A thuộc \(y=\left(m-1\right)x+m^2-1\) thì:
\(-1.\left(m-1\right)+m^2-1=2\)
\(\Leftrightarrow m^2-m-2=0\Rightarrow\left[{}\begin{matrix}m=-1\left(loại\right)\\m=2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
trên mặt phẳn toạ độ Oxy cho parabol (P):y=x^2 và đường thẳng (d): y=2(m 1)x-2m 4 a)tìm toạ độ giao điểm của (P) và (d) khi m=2 b) gọi x1 và x2 là hoành độ các giao điểm của (P) và (d).cm biểu thức A=x1(1-x2/2) x2(1-x1/2) không phụ thuộc m
Xem chi tiết
Gọi (d1) là đồ thị hàm số y = m x + 2 và
(d2) là đô thị hàm số y = 1 x – 1 2
a) Với m = - 12 , xác định toạ độ giao điểm của (d1) và (d2)
b) Xác định giá trị của m để M(- 3; - 3) là giao điểm của (d1) , (d2)
Gọi M, N là giao điểm của đồ thị
y
7
x
+
6
x
-
2
và đường thẳng yx+2. Khi đó hoành độ trung điểm của đoạn MN bằng A.
7
2
B.
-
11
2
C.
11
2
D. ...
Đọc tiếp
Gọi M, N là giao điểm của đồ thị y = 7 x + 6 x - 2 và đường thẳng y=x+2. Khi đó hoành độ trung điểm của đoạn MN bằng
A. 7 2
B. - 11 2
C. 11 2
D. - 7 2
Gọi M, N là giao điểm của đồ thị
y
7
x
+
6
x
−
2
và đường thẳng
y
x
+
2
. Khi đó hoành độ trung điểm của đoạn MN bằng A.
7
2
B.
−
11
2
C.
11...
Đọc tiếp
Gọi M, N là giao điểm của đồ thị y = 7 x + 6 x − 2 và đường thẳng y = x + 2 . Khi đó hoành độ trung điểm của đoạn MN bằng
A. 7 2
B. − 11 2
C. 11 2
D. − 7 2
Đáp án A
Xét phương trình hoành độ giao điểm của 2 đồ thị
Đúng 0
Bình luận (0)
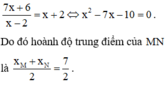
cho hàm số y=f(x) = -x+m-2 (d)
gọi x1,x2 là hoành dộ giao điểm của đường thẳng (d) và parapol y=x2. tìm m để x12x22 - 4x1 - 4x2 = 4
Xét phương trình hoành độ giao điểm của (d) và (P):
x2 + x - m + 2 = 0
Phương trình có nghiệm ⇔ △ ≥ 0 ⇔ 1-4(2-m) ≥ 0 ⇔ 4m-7 ≥ 0 ⇔ m ≥ 1,75
Theo hệ thức Vi-ét có: \(\left\{{}\begin{matrix}x_1+x_2=-1\\x_1.x_2=2-m\end{matrix}\right.\)
=> x12.x22 - 4x1 - 4x2 = 4 ⇔ x12.x22 - 4(x1 + x2) = 4
⇔ (2 - m)2 - 4.(-1) = 4
⇔ (2 - m)2 + 4 = 4
⇔ (2 - m)2 = 0
⇔ 2 - m = 0
⇔ m = 2 (t/m)
Đúng 2
Bình luận (0)
Gọi M, N là các giao điểm của đường thẳng
y
x
−
4
với đồ thị của hàm số
y
−
2
x
+
5
x
−
2
. Tìm tọa độ trung điểm I của MN? A.
I
2
;
−
2...
Đọc tiếp
Gọi M, N là các giao điểm của đường thẳng y = x − 4 với đồ thị của hàm số y = − 2 x + 5 x − 2 . Tìm tọa độ trung điểm I của MN?
A. I 2 ; − 2
B. I 1 ; − 3
C. I 3 ; − 1
D. I − 2 ; 2
Đáp án A
Hoành độ giao điểm là nghiệm của PT:
x − 4 = − 2 x + 5 x − 2 ⇔ x 2 − 6 x + 8 = − 2 x + 5 x ≠ 2
⇔ x 2 − 4 x − 13 = 0 . Vậy trung điểm I của MN có hoành độ x = 2 ⇒ y = − 2 .
Đúng 0
Bình luận (0)