Cho hai số thực dương a, b với a khác 1. Đặt M = log a b . Tính M theo N = log a b .
A. M = N
B. M = 2N
C. M = 1 2 N
D. M = N 2
Giả sử đã cho \({\log _a}M\) và ta muốn tính \({\log _b}M.\) Để tìm mối liên hệ giữa \({\log _a}M\) và \({\log _b}M,\) hãy thực hiện các yêu cầu sau:
a) Đặt \(y = {\log _a}M,\) tính M theo y;
b) Lấy loogarit theo cơ số b cả hai vế của kết quả nhận được trong câu a, từ đó suy ra công thức mới để tính y.
a) \(y = {\log _a}M \Leftrightarrow M = {a^y}\)
b) Lấy loogarit theo cơ số b cả hai vế của \(M = {a^y}\) ta được
\({\log _b}M = {\log _b}{a^y} \Leftrightarrow {\log _b}M = y{\log _b}a \Leftrightarrow y = \frac{{{{\log }_b}M}}{{{{\log }_b}a}}\)
Hoạt động 5
Cho ba số thực dương a, b, c với \(a \ne 1\,;\,c \ne 1\)
a) Bằng cách sử dụng tính chất \(b = {a^{{{\log }_a}b}}\), chứng tỏ rằng \({\log _c}b = {\log _a}b.{\log _c}a\)
b) So sánh \({\log _a}b\,\,\,và \frac{{{{\log }_c}b}}{{{{\log }_c}a}}\)
a) \({\log _c}b = {\log _a}b.{\log _c}a \Leftrightarrow {a^{{{\log }_c}b}} = {a^{{{\log }_a}b.{{\log }_c}a}} \Leftrightarrow {c^{{{\log }_c}b}} = {\left( {{c^{{{\log }_c}a}}} \right)^{{{\log }_a}b}} \Leftrightarrow b = {a^{{{\log }_a}b}} \Leftrightarrow b = b\) (luôn đúng)
Vậy \({\log _c}b = {\log _a}b.{\log _c}a\)
b) Từ \({\log _c}b = {\log _a}b.{\log _c}a \Leftrightarrow {\log _a}b = \frac{{{{\log }_c}b}}{{{{\log }_c}a}}\)
Cho hai số thực dương a, b với \(a \ne 1\). Khẳng định nào sau đây là đúng?
A. \({\log _a}\left( {{a^3}{b^2}} \right) = 3 + {\log _a}b\).
B. \({\log _a}\left( {{a^3}{b^2}} \right) = 3 + 2{\log _a}b\).
C. \({\log _a}\left( {{a^3}{b^2}} \right) = \frac{3}{2} + {\log _a}b\).
D. \({\log _a}\left( {{a^3}{b^2}} \right) = \frac{1}{3} + \frac{1}{2}{\log _a}b\).
\(log_a\left(a^3b^2\right)=log_aa^3+log_ab^2=3+2\cdot log_ab\)
=>B
1) Cho a,b là các số thực dương khác 1 và thoả mãn ab khác 1. Rút gọn biểu thức sau: P=(logab + logba + 2)(logab - logabb).logba - 1
Cho các số thực dương a,b thỏa mãn log a = x , log b = y . Tính P = log ( a 2 b 3 )
![]()
![]()
![]()
![]()
Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số lôgarit \(y = {\log _a}x;\,y = {\log _b}x;\,y = {\log _c}x\) được cho bởi Hình 15. Kết luận nào sau đây là đúng với ba số a, b, c?
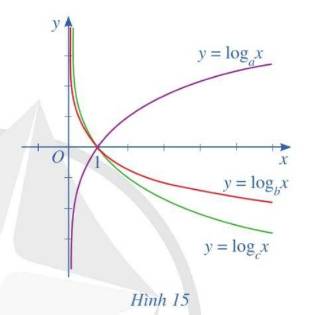
A. c < a < b
B. c < b < a
C. a < b < c
D. b < c < a
Cho bốn số thực dương a, b, x, y với \(a,b \ne 1\). Khẳng định nào sau đây là sai?
A. \({\log _a}(xy) = {\log _a}x + {\log _b}y\).
B. \({\log _a}\frac{x}{y} = {\log _a}x - {\log _a}y\).
C. \({\log _a}\frac{1}{x} = \frac{1}{{{{\log }_a}x}}\).
D. \({\log _a}b \cdot {\log _b}x = {\log _a}x\).
Đề bài
Cho hai số thực dương a, b thỏa mãn \({a^3}{b^2} = 100\). Tính giá trị của biểu thức \(P = 3\log a + 2\log b\)
\(P=loga^3+logb^2=log\left(a^3b^2\right)=log\left(100\right)=10\)
Giả sử a, b là các số thực sao cho x3 + y3 = a.103x + b.102x đúng với mọi số thực dương x, y, z thỏa mãn log (x + y) = z và log(x2 + y2) = z + 1. Giá trị của a+b bằng:
A. - 31 2
B. - 25 2
C. 31 2
D. 29 2
Đáp án D.
Ta có
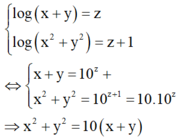
Khi đó
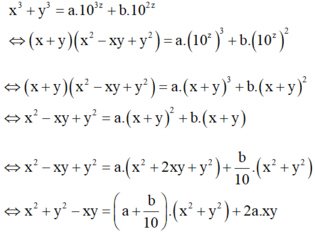
Đồng nhất hệ số, ta được
