Lập phương trình đường tròn đi qua ba điểm:
a, A(1; 2), B(5; 2), C(1; -3)
b, M(-2; 4), N(5; 5), P(6; -2)
Lập phương trình đường tròn đi qua ba điểm A(1; 2), B(5; 2), C(1 ; – 3).
Giả sử tâm đường tròn là điểm \(I\left( {a;b} \right)\). Ta có: \(IA = IB = IC \Leftrightarrow I{A^2} = I{B^2} = I{C^2}\)
Vì \(I{A^2} = I{B^2},I{B^2} = I{C^2}\) nên: \(\left\{ \begin{array}{l}{\left( {1 - a} \right)^2} + {\left( {2 - b} \right)^2} = {\left( {5 - a} \right)^2} + {\left( {2 - b} \right)^2}\\{\left( {5 - a} \right)^2} + {\left( {2 - b} \right)^2} = {\left( {1 - a} \right)^2} + {\left( { - 3 - b} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 3\\b = \frac{{ - 1}}{2}\end{array} \right.\)
Vậy \(I\left( {3; - \frac{1}{2}} \right)\) và \(R = IA = \sqrt {{{\left( { - 2} \right)}^2} + {{\left( {\frac{5}{2}} \right)}^2}} = \frac{{\sqrt {41} }}{2}\)
Vậy phương trình đường tròn đi qua 3 điểm A,B, C là: \({\left( {x - 3} \right)^2} + {\left( {y + \frac{1}{2}} \right)^2} = \frac{{41}}{4}\)
Lập phương trình đường tròn đi qua ba điểm: A(1; 2); B(5; 2); C(1; -3)
Sử dụng phương trình đường tròn : x2 – y2 – ax – 2by +c = 0
Đường tròn đi qua điểm A(1; 2):
12 + 22 – 2a -4b + c = 0 <=> 2a + 4b – c = 5
Đường tròn đi qua điểm B(5; 2):
52 + 22 – 10a -4b + c = 0 <=> 10a + 4b – c = 29
Đường tròn đi qua điểm C(1; -3):
12 + (-3)2 – 2a + 6b + c = 0 <=> 2a – 6b – c = 10
Để tìm a, b, c ta giải hệ:
Lấy (2) trừ cho (1) ta được phương trình: 8a = 24 => a = 3
Lấy (3) trừ cho (1) ta được phương trình: -10b = 5 => b = – 0,5
Thế a = 3 ; b = -0.5 vào (1) ta tính được c = -1
Ta được phương trình đường tròn đi qua ba điểm A, B, C là :
x2 + y2 – 6x + y – 1 = 0
Chú ý:
Tâm I(x; y) của đường tròn đi qua ba điểm A, B, C là điểm cách đều ba điểm ấy, hay
IA = IB = IC => IA2 = IB2 = IC2
Từ đây suy ra x, y là nghiệm của hệ:
<=> I(3; )
Từ đây ta tìm được R và viết được phương trình đường tròn.
Cho A(-3;4) B(2;1) C(-4;5)
a lập phương trình tổng quát của AC
b, lập phương trình đường tròn tâm B tiếp xúc AC
c, lập phương trình tổng quát đường cao AH
d, lập phương trình đường trung tuyến AM
e, Lập phương trình đường tròn đi qua A B C
Trong mặt phẳng tọa độ cho hai điểm A(3;0), B(0;2) và đường thẳng d: x + y = 0.
a) Lập phương trình tham số của đường thẳng Δ đi qua A và song song với d
b) Lập phương trình đường tròn đi qua A,B và có tâm thuộc đường thẳng d
c) Lập phương trình chính tắc của elip đi qua điểm B và có tâm sai e = 5 3
Đường thẳng Δ song song với d ⇒ Δ: x + y + c = 0, (c ≠ 0)
Vì Δ đi qua A ⇒ 3 + 0 + c = 0 ⇒ c = -3(tm)
Vậy đường thẳng Δ có dạng: x+y-3=0
Vì đường tròn có tâm I thuộc d nên I(a;-a)
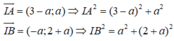
Vì đường tròn đi qua A, B nên I A 2 = I B 2 ⇒ (3 - a ) 2 + a 2 = a 2 + (2 + a ) 2 ⇔ (3 - a ) 2 = (2 + a ) 2
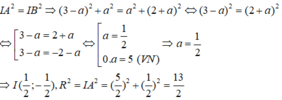
Vậy phương trình đường tròn có dạng:
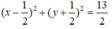
Ta có:
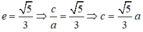
Giả sử elip (E) có dạng:
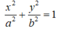
Vì (E) đi qua B nên:
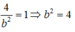
Mà
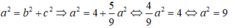
Vậy phương trình chính tắc của elip (E) là:
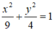
Phương trình đường tròn đi qua ba điểm A(1; 2), B(-1; 1), C(2;3) là:
A. x 2 + y 2 + 5 x − 13 y + 16 = 0
B. x 2 + y 2 + 5 x − 13 y − 16 = 0
C. x 2 + y 2 + 5 2 x − 13 2 y + 16 = 0
D. x 2 + y 2 + 5 2 x − 13 2 y − 16 = 0
Gọi phương trình đường tròn là x 2 + y 2 − 2 a x − 2 b y + c = 0 . Do đường tròn qua A(1;2),
B( -1;1), C(2;3) nên ta có
1 2 + 2 2 − 2.1. a − 2.2. b + c = 0 − 1 2 + 1 2 − 2. − 1 . a − 2.1. b + c = 0 2 2 + 3 2 − 2.2. a − 2.3. b + c = 0 ⇔ − 2 a − 4 b + c = − 5 2 a − 2 b + c = − 2 − 4 a − 6 b + c = − 13 ⇔ a = − 5 2 b = 13 2 c = 16
Phương trình đường tròn là: x 2 + y 2 + 5 x – 13 y + 16 = 0
ĐÁP ÁN A
Phương trình đường tròn đi qua ba điểm A(-1; 3), B(1; 0), C(3; 5) là:
A. x 2 + y 2 - 5 / 8 x - 11 / 4 y + 21 / 8 = 0
B. x 2 + y 2 - 27 / 8 x - 21 / 4 y + 19 / 8 = 0
C. x 2 + y 2 - 5 / 6 x - 11 / 6 x - 2 / 3 = 0
D. x 2 + y 2 - 27 / 8 x - 21 / 4 y - 19 / 8 = 0
Phương trình đường tròn đi qua ba điểm A(-1; 3), B(1; 4), C(3; 2) là:
A. x 2 + y 2 − 5 3 x − 11 3 y + 2 3 = 0
B. x 2 + y 2 − 5 3 x − 11 3 y − 2 3 = 0
C. x 2 + y 2 − 5 6 x − 11 6 y − 2 3 = 0
D. x 2 + y 2 − 5 6 x − 11 6 y + 2 3 = 0
Gọi phương trình đường tròn là . x 2 + y 2 − 2 a x − 2 b y + c = 0
Do đường tròn qua A(-1; 3), B(1; 4), C(3; 2) nên ta có
− 1 2 + 3 2 − 2. − 1 a − 2.3 b + c = 0 1 2 + 4 2 − 2.1. a − 2.4 b + c = 0 3 2 + 2 2 − 2.3 a − 2.2 b + c = 0
⇒ 2 a − 6 b + c = − 10 − 2 a − 8 b + c = − 17 − 6 a − 4 b + c = − 13 ⇔ a = 5 6 b = 11 6 c = − 2 3
Phương trình đường tròn là x 2 + y 2 − 5 3 x − 11 3 y − 2 3 = 0 . Đáp án B.
Chú ý. Học sinh có thể tìm tâm và bán kính trước rồi suy ra phương trình của đường tròn, tuy nhiên cách làm này dài hơn. Khi có phương trình tổng quát của đường tròn rồi thì có ngay thông tin của tâm và bán kính của đường tròn.
Phương trình của đường tròn (C) đi qua ba điểm A(0;4), B(2;4), C(4;0) có phương trình:
A. x 2 + y 2 - 8x + 2y - 1 = 0
B. x 2 + y 2 - 2x + 8y - 1 = 0
C. x 2 + y 2 - 2x - 2y - 8 = 0
D. x 2 + y 2 - 8x - 6y - 2 = 0
Đáp án: C
Giả sử (C) có dạng: x 2 + y 2 - 2ax - 2by + c = 0
Vì 3 điểm A, B, C thuộc đường tròn (C) nên ta có hệ phương trình:
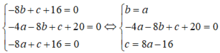
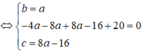
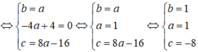
Vậy phương trình đường tròn (C) có dạng: x 2 + y 2 - 2x - 2y - 8 = 0
trong mặt phẳng Oxy cho ba điểm A(0;4), B(3;4), C(3;0)
a viết phương trình đường tròn (C) đi qua ba điểm A,B,C
b viết phương trình đường tròn (C) tâm C, tiếp xúc đường thẳng (d) 3x+4y-5=0
a.
Gọi phương trình đường tròn (C) có dạng:
\(x^2+y^2-ax-by+c=0\)
Do A;B;C thuộc (C) nên: \(\left\{{}\begin{matrix}0+16-0.a-4b+c=0\\9+16-3a-4b+c=0\\9+0-3a-0.b+c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-4b+c=-16\\-3a-4b+c=-25\\-3a+c=-9\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=3\\b=4\\c=0\end{matrix}\right.\)
Hay pt (C) có dạng: \(x^2+y^2-3x-4y=0\)
b.
Đường tròn (C) tiếp xúc (d) nên có bán kính \(R=d\left(C;d\right)=\dfrac{\left|3.3+0.4-5\right|}{\sqrt{3^2+4^2}}=\dfrac{4}{5}\)
Phương trình: \(\left(x-3\right)^2+y^2=\dfrac{16}{25}\)