Chỉ ra khoảng đồng biến, nghịch biến của hàm số : y = ax + b, trong mỗi trường hợp a > 0 ; a < 0.

Những câu hỏi liên quan
Chỉ ra khoảng đồng biến, nghịch biến của hàm số: y = ax2 + bx + c, trong mỗi trường hợp a > 0 ; a < 0.
Chỉ ta khoảng đồng biến, khoảng nghịch biến của hàm số \(y=ax^2+bx+c\) trong mỗi trường hợp \(a>0;a< 0\) ?
Nếu \(a>0\) thì hàm số \(y=ax^2+bx+c\)
Nghịch biến trên khoảng: \(\left(-\infty;-\dfrac{b}{2a}\right)\);
Đồng biến trên khoảng: \(\left(\dfrac{-b}{2a};+\infty\right)\).
Nếu \(a< 0\) thì hàm số \(y=ax^2+bx+c\):
Nghịch biến trên khoảng: \(\left(\dfrac{-b}{2a};+\infty\right)\);
Đồng biến trên khoảng: \(\left(-\infty;-\dfrac{b}{2a}\right)\).
Đúng 0
Bình luận (0)
Chỉ ra khoảng đồng biến, khoảng nghịch biến của hàm số \(y=ax+b\) ?
a > 0
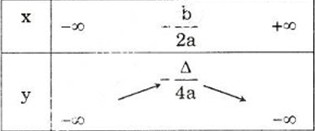
Hàm số đồng biến trên (-∞,\(\dfrac{-b}{2a}\))
Hàm số nghịch biến trên (\(\dfrac{-b}{2a}\), +∞)
a < 0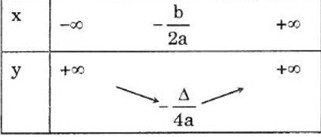
Hàm số đồng biến trên (\(\dfrac{-b}{2a}\), +∞)
Hàm số nghịch biến trên (-∞,\(\dfrac{-b}{2a}\))
Đúng 0
Bình luận (0)
Từ đồ thị hàm số bậc hai cho ở hai hình sau, tìm khoảng đồng biến và nghịch biến của hàm số trong mỗi trường hợp.
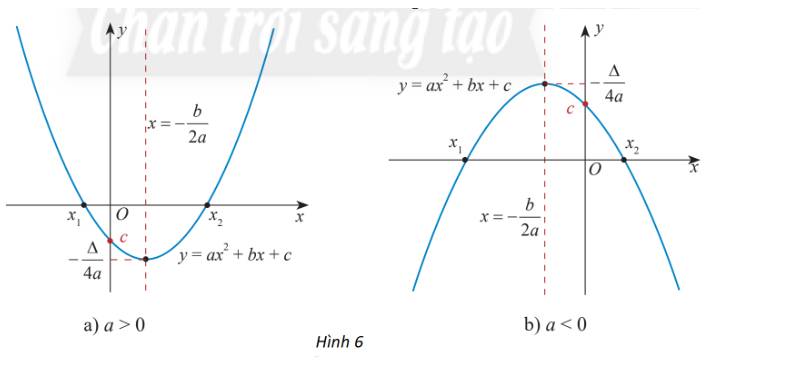
a)
Trên \(( - \infty ; - \frac{b}{{2a}})\) đồ thị có dạng đi xuống từ trái sang phải nên hàm số đó nghịch biến trên \(( - \infty ; - \frac{b}{{2a}})\)
Trên \(( - \frac{b}{{2a}}; + \infty )\) đồ thị có dạng đi lên từ trái sang phải nên hàm số đó đồng biến trên \(( - \frac{b}{{2a}}; + \infty )\)
Vậy hàm số có khoảng đồng biến là \(( - \frac{b}{{2a}}; + \infty )\), khoảng nghịch biến là \(( - \infty ; - \frac{b}{{2a}})\)
b)
Trên \(( - \infty ; - \frac{b}{{2a}})\) đồ thị có dạng đi lên từ trái sang phải nên hàm số đó đồng biến trên \(( - \infty ; - \frac{b}{{2a}})\)
Trên \(( - \frac{b}{{2a}}; + \infty )\) đồ thị có dạng đi xuống từ trái sang phải nên hàm số đó nghịch biến trên \(( - \frac{b}{{2a}}; + \infty )\)
Vậy hàm số có khoảng đồng biến là \(( - \infty ; - \frac{b}{{2a}})\), khoảng nghịch biến là \(( - \frac{b}{{2a}}; + \infty )\)
Đúng 0
Bình luận (0)
c/m tính chất đồng biến nghịch biến của hàm số y= ax2 trong các trường hợp sau
TH1: nếu a>0 => đồng biến khi x thuộc R+
TH2: nếu a<0 => nghịch biến khi x thuộc R+
TH3: nếu a<0 => đồng biến khi x thuộc R-
TH1: Lấy \(x_1;x_2\in R\) sao cho \(0< x_1< x_2\)
\(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{a\cdot\left(x_1^2-x_2^2\right)}{x_1-x_2}=a\cdot\left(x_1+x_2\right)\)>0 vì \(x_1+x_2>0;a>0\)
=>Hàm số y=f(x)=ax2 đồng biến khi x>0 nếu a>0
TH2: Lấy \(x_1;x_2\in R^+;0< x_1< x_2\)
\(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{a\cdot\left(x_1^2-x_2^2\right)}{x_1-x_2}=\dfrac{a\left(x_1-x_2\right)\left(x_1+x_2\right)}{x_1-x_2}\)
\(=a\left(x_1+x_2\right)< 0\)(vì x1+x2>0 và a<0)
=>Hàm số nghịch biến khi x>0
TH3: Lấy \(x_1;x_2\in R^-\) sao cho \(x_1< x_2< 0\)
\(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{a\left(x_1^2-x_2^2\right)}{x_1-x_2}=\dfrac{a\left(x_1+x_2\right)\left(x_1-x_2\right)}{x_1-x_2}\)
\(=a\left(x_1+x_2\right)>0\) vì a<0 và x1+x2<0
=>Hàm số đồng biến khi x<0
Đúng 0
Bình luận (0)
Vẽ đồ thị của các hàm số \(y=3x+1\) và \(y=-2x^2\). Hãy cho biết:
a) Hàm số \(y=3x+1\) đồng biến hay nghịch biến trên R.
b) Hàm số \(y=-2x^2\) đồng biến hay nghịch biến trên mỗi khoảng: \(\left(-\infty;0\right)\) và \(\left(0;+\infty\right)\)
Vẽ đồ thị \(y = 3x + 1;y = - 2{x^2}\)

a) Trên \(\mathbb{R}\), đồ thị \(y = 3x + 1\) đi lên từ trái sang phải, như vậy hàm số \(y = 3x + 1\) đồng biến trên \(\mathbb{R}\)
b) Trên khoảng \(\left( { - \infty ;0} \right)\), đồ thị \(y = - 2{x^2}\)đi lên từ trái sang phải với mọi \(x \in \left( { - \infty ;0} \right)\) , như vậy hàm số đồng biến trên \(\left( { - \infty ;0} \right)\)
Trên khoảng \(\left( {0; + \infty } \right)\), đồ thị \(y = - 2{x^2}\)đi xuống từ trái sang phải với mọi \(x \in \left( {0; + \infty } \right)\) , như vậy hàm số nghịch biến trên \(\left( {0; + \infty } \right)\)
Đúng 0
Bình luận (0)
Vẽ đồ thị các hàm số sau và chỉ ra các khoảng đồng biến, nghịch biến của chúng.
a) \(y=-2x+1\);
b) \(y=-\dfrac{1}{2}x^2.\)

Nhìn vào đồ thị, ta thấy:
a) Hàm số \(y = - 2x + 1\)nghịch biến trên \(\mathbb{R}\)
b) Hàm số \(y = - \frac{1}{2}{x^2}\) đồng biến trên khoảng \(\left( { - \infty ;0} \right)\); nghịch biến trên khoảng \(\left( {0; + \infty } \right)\)
Đúng 0
Bình luận (0)
Cho hàm số \(y = f\left( x \right)\) có đồ thị như Hình 9. Chỉ ra khoảng đồng biến và khoảng nghịch biến của hàm số \(y = f\left( x \right)\).
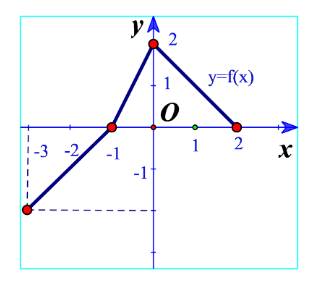
Từ đồ thị hàm số ta thấy khi x tăng từ -3 đến -1 và từ -1 đến 0 thì đồ thị đi lên nên hàm số đồng biến trên các khoảng (-3;-1) và (-1;0).
Khi x tăng từ 0 đến 2 thì đồ thị đi xuống nên hàm số nghịch biến trên (0;2).
Đúng 0
Bình luận (0)
Cho hàm số y = ax = b (a ≠ 0).
a) Khi nào thì hàm số đồng biến?
b) Khi nào thì hàm số nghịch biến?
a) Hàm số đồng biến khi a > 0
b) Hàm số nghịch biến khi a < 0
Đúng 0
Bình luận (0)













