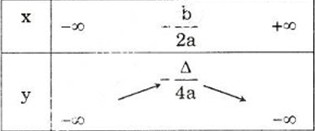
Hàm số đồng biến trên (-∞,\(\dfrac{-b}{2a}\))
Hàm số nghịch biến trên (\(\dfrac{-b}{2a}\), +∞)
a < 0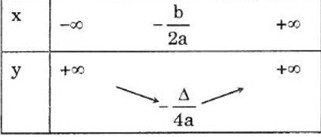
Hàm số đồng biến trên (\(\dfrac{-b}{2a}\), +∞)
Hàm số nghịch biến trên (-∞,\(\dfrac{-b}{2a}\))

Hàm số đồng biến trên (-∞,\(\dfrac{-b}{2a}\))
Hàm số nghịch biến trên (\(\dfrac{-b}{2a}\), +∞)
a < 0
Hàm số đồng biến trên (\(\dfrac{-b}{2a}\), +∞)
Hàm số nghịch biến trên (-∞,\(\dfrac{-b}{2a}\))
Chỉ ta khoảng đồng biến, khoảng nghịch biến của hàm số \(y=ax^2+bx+c\) trong mỗi trường hợp \(a>0;a< 0\) ?
Thế nào là hàm số đồng biến (nghịch biến) trên khoảng (a; b) ?
Cho hàm số y=x^2 +bx+c có đồ thị P , P đi qua A(0;6) có trục đối xứng x=1 Tìm các khoảng đồng biến , nghịch biến và vẽ đồ thị x= -x^2+4x
Cho hàm số \(y=f\left(x\right)\) nghịch biến trên khoảng \(\left(a;b\right)\), khi đó hàm số \(y=-f\left(x\right)\) có chiều biến thiên như thế nào trên khoảng \(\left(a;b\right)\) ?
Tìm tất cả số nguyên a sao cho hàm số f(x)= ax+ \(\sqrt{a+5}\) nghịch biến trên R
Tìm tất cả số nguyên a sao cho hàm số f(x)= ax+ \(\sqrt{a+5}\) nghịch biến trên R
Cho hai hàm số f(x) và g(x) cùng đồng biến trên khoảng (a;b). Có thể kết luận gì về chiều biến thiên của hàm số y=f(x)+g(x) trên khoảng (a;b)? Giải thích.
Tìm tất cả các giá trị của tham số m để hàm số y= -x2 + 2(m-1)x + 3 nghịch biến trên khoảng (1; dương vô cùng).
1. Trong các hàm số sau , hàm số nào tăng trên khoảng ( -1;0)
A. y =x
B. y = 1/x
C. y = |x|
D. y = x^2
2. Tìm điều kiện của tham số để các hàm số f(x) = ax^2 + bx +C là hàm số chẵn.
A. a tùy ý , b =0 , C=0
B. a tùy ý , b=0 , c tùy ý
C. a,b,C tùy ý
D. a tùy ý , b tùy ý,C =0
3. Trồng các hàm số sau , hàm nào nghịch biến trên R
A. y = -πx +3
B. y = 2x +3
C. y = πx -2
D. y =2
15. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ -2017;2017] đề hàm số y = (m-2)x +2m đồng biến trên R
A. 2015
B. 2016
C. Vô số
D. 2014