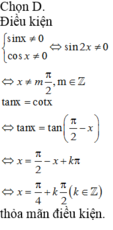Giải các phương trình sau cotx - cot2x = tanx + 1

Những câu hỏi liên quan
giải phương trình
\(\frac{1}{tanx+cot2x}=\frac{\sqrt{2}\left(cosx-sinx\right)}{cotx-1}\)
ĐKXĐ: \(\left\{{}\begin{matrix}sinx\ne0\\cosx\ne0\\cotx\ne1\end{matrix}\right.\)
\(\frac{1}{\frac{sinx}{cosx}+\frac{cos2x}{sin2x}}=\frac{\sqrt{2}\left(cosx-sinx\right)}{\frac{cosx}{sinx}-1}\)
\(\Leftrightarrow\frac{sin2x.cosx}{cos2x.cosx+sin2x.sinx}=\frac{\sqrt{2}sinx\left(cosx-sinx\right)}{cosx-sinx}\)
\(\Leftrightarrow\frac{sin2x.cosx}{cosx}=\sqrt{2}sinx\)
\(\Leftrightarrow2sinx.cosx=\sqrt{2}sinx\)
\(\Leftrightarrow cosx=\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+k2\pi\left(l\right)\\x=-\frac{\pi}{4}+k2\pi\end{matrix}\right.\)
Vậy \(x=-\frac{\pi}{4}+k2\pi\)
Giải phương trình sau: tanx – 2.cotx + 1 = 0
Điều kiện 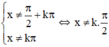
tanx – 2.cotx + 1 = 0
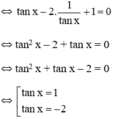
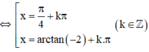 (Thỏa mãn điều kiện).
(Thỏa mãn điều kiện).
Vậy phương trình có tập nghiệm
{ + kπ; arctan(-2) + kπ} (k ∈ Z)
+ kπ; arctan(-2) + kπ} (k ∈ Z)
Đúng 0
Bình luận (0)
Giải các phương trình sau:
\(a,cos3x=-cos\left(x+\dfrac{\pi}{3}\right)\)
\(b,tanx+cotx=0\)
a) cos3x = \(cos\left(\pi-x-\dfrac{\pi}{3}\right)\)
<=> cos3x = \(cos\left(\dfrac{2\pi}{3}-x\right)\)
<=> 3x = \(\dfrac{2\pi}{3}-x\) hoặc 3x = \(\dfrac{-2\pi}{3}+x\)
<=> 4x = \(\dfrac{2\pi}{3}+k2\pi\) hoặc 2x = \(\dfrac{-2\pi}{3}+k2\pi\)
<=> x = \(\dfrac{\pi}{6}+\dfrac{k\pi}{2}\) hoặc x = \(\dfrac{-\pi}{3}+k\pi\)
<=> x = \(\left\{\dfrac{\pi}{6}+\dfrac{k\pi}{2};\dfrac{-\pi}{3}+k\pi;k\in Z\right\}\)
b ) Điều kiện sinx\(\ne0;cosx\ne0\)
<=> sin2x\(\ne0\) <=> x \(\ne\dfrac{k\pi}{2}\);k\(\in Z\)
tanx + cotx =0
<=> tan2x + tanx =0
<=> tanx(tanx+1)=0
<=> tanx=0 hoặc tanx = -1
<=> x=\(k\pi\) (loại) hoặc x = \(\dfrac{-\pi}{4}+k\pi\)
Vậy x = \(\dfrac{-\pi}{4}+k\pi;k\in Z\)
Đúng 0
Bình luận (0)
Giải phương trình
c
o
t
x
-
1
cos
2
x
1
+
tan
x
+
sin
2
x
-
1
2
sin...
Đọc tiếp
Giải phương trình c o t x - 1 = cos 2 x 1 + tan x + sin 2 x - 1 2 sin 2 x
Điều kiện của phương trình: sinx ≠ 0, cos ≠ 0, tan ≠ -1.
Biến đổi tương đương đã cho, ta được
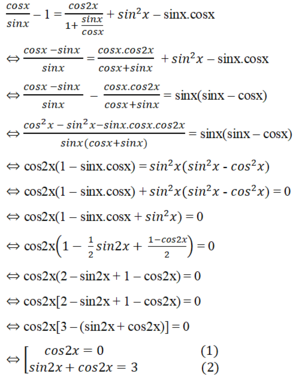
Phương trình (2) vô nghiệm vì |sin2x + cos2x| ≥ √2.
Phương trình (1) có nghiệm 2x = π/2+kπ,k ∈ Z
⇒ x = π/4+ k π/2,k ∈ Z.
Giá trị x = π/4+ k π/2, k = 2n + 1,
với n ∈ Z bị loại do điều kiện tanx ≠ -1.
Đúng 0
Bình luận (0)
Giải phương trình : tanx + cotx=2
ĐKXĐ: \(x\ne k\dfrac{\pi}{2}\)
\(tanx+\dfrac{1}{tanx}=2\)
\(\Rightarrow tan^2x+1=2tanx\)
\(\Leftrightarrow\left(tanx-1\right)^2=0\)
\(\Leftrightarrow tanx=1\)
\(\Rightarrow x=\dfrac{\pi}{4}+k\pi\) (thỏa mãn)
Đúng 0
Bình luận (0)
Giải phương trình cotx - tanx + 4sin2x = 2/sin2x
Đối với những phương trình lượng giác chứa tanx, cotx, sin2x hoặc cos2x, ta có thể đưa về phương trình chứa cosx, sinx, sin2x, hoặc cos2x ngoài ra cũng có thể đặt ẩn phụ t = tanx để đưa về một phương trình theo t.
Cách 1: Điều kiện của phương trình:
sin2x ≠ 0 ⇔ cos2x ≠ 1 hoặc cos2x ≠ -1 (1)
Ta có:
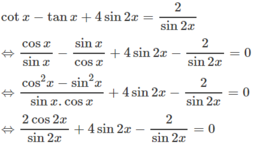
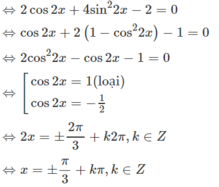
Cách 2. Đặt t = tanx
Điều kiện t ≠ 0
Phương trình đã cho có dạng
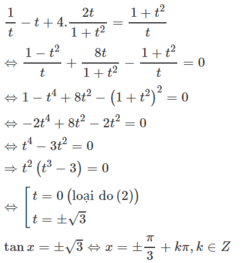
Đúng 0
Bình luận (0)
Giải phương trình: \(cotx-tanx-2tan2x=1\)
giải phương trình: sin^4x+cos^4x/sin2x=1/2(tanx+cotX)
Tất cả các nghiệm của phương trình tanx=cotx là
![]()
![]()
![]()
![]()