Điều kiện 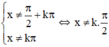
tanx – 2.cotx + 1 = 0
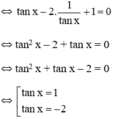
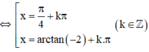 (Thỏa mãn điều kiện).
(Thỏa mãn điều kiện).
Vậy phương trình có tập nghiệm
{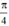 + kπ; arctan(-2) + kπ} (k ∈ Z)
+ kπ; arctan(-2) + kπ} (k ∈ Z)
Điều kiện 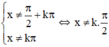
tanx – 2.cotx + 1 = 0
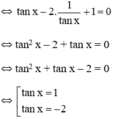
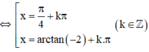 (Thỏa mãn điều kiện).
(Thỏa mãn điều kiện).
Vậy phương trình có tập nghiệm
{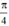 + kπ; arctan(-2) + kπ} (k ∈ Z)
+ kπ; arctan(-2) + kπ} (k ∈ Z)
Giải các phương trình sau cotx - cot2x = tanx + 1
Giải phương trình cotx - tanx + 4sin2x = 2/sin2x
Giải phương trình c o t x - 1 = cos 2 x 1 + tan x + sin 2 x - 1 2 sin 2 x
Tập nghiệm của phương trình tanx + cotx -2 = 0 là:
A. {-π/4+kπ,k∈Z}
B. {π/4+kπ,k∈Z}
C. {±π/4+k2π,k∈Z}
D. ∅
Tính tổng tất cả các nghiệm của phương trình tanx+cotx = 4 3 3 trên đoạn 0 ; π
A. π 2
B. 3 π 2
C. π 3
D. 2 π 3
Tính tổng tất cả các nghiệm của phương trình tan x + c o t x = 4 3 3 trên đoạn 0 ; π
A. π 2
B. 3 π 2
C. π 3
D. 2 π 3
Tính tổng tất cả các nghiệm của phương trình tan x + c o t x = 4 3 3 trên đoạn 0 ; π
A. π 2
B. 3 π 2
C. π 3
D. 2 π 3
Nghiệm của phương trình tanx + cotx = - 2 là
![]()
![]()
![]()
![]()
Nghiệm của phương trình tan x + c o t x = sin 2 x – 1 là:
A. x = π 4 + k 2 π , k ∈ ℤ
B. x = - π 4 + k π , k ∈ ℤ
C. x = - π 4 + k 2 π , k ∈ ℤ
D. x = π 4 + k π , k ∈ ℤ