Hàm số y = x n + x n - 1 + . . . + x = 1 ( n ∈ ℕ , n ⩾ 1 ) có đạo hàm tại x=1 bằng
A . n ( n + 1 ) 2
B . n ( n - 1 ) 2
C . n ( n - 1 )
D . n ( n + 1 )
cho hàm số: \(y=\left(2m-1\right)x+n\) với \(\left(m\ne\dfrac{1}{2}\right)\)
Tìm giá trị của m, n biết n=2m và đồ thị hàm số \(y=\left(2m-1\right)x+n\) cắt đồ thị hàm số \(y=\dfrac{1}{2}x-4\) tại một điểm trên trục tung
Vì hai đồ thị cắt nhau tại một điểm trên trục tung nên n=-4
=>m=-2
a) Dùng định nghĩa tỉnh đạo hàm của hàm số \(y = x\) tại điểm \(x = {x_0}\).
b) Nhắc lại đạo hàm của các hàm số \(y = {x^2},y = {x^3}\) đã tìm được ở bài học trước. Từ đó, dự đoán đạo hàm của hàm số \(y = {x^n}\) với \(n \in {\mathbb{N}^*}\).
a) Với bất kì \({x_0} \in \mathbb{R}\), ta có:
\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{x - {x_0}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} 1 = 1\)
Vậy \(f'\left( x \right) = {\left( x \right)^\prime } = 1\) trên \(\mathbb{R}\).
b) Ta có:
\(\begin{array}{l}{\left( {{x^2}} \right)^\prime } = 2{\rm{x}}\\{\left( {{x^3}} \right)^\prime } = 3{{\rm{x}}^2}\\...\\{\left( {{x^n}} \right)^\prime } = n{{\rm{x}}^{n - 1}}\end{array}\)
a) Tính đạo hàm của hàm số \(y = {x^3}\) tại điểm x bất kì.
b) Dự đoán công thức đạo hàm của hàm số \(y = {x^n}\left( {n \in {\mathbb{N}^*}} \right)\)
a) Với \({x_0}\) bất kì, ta có:
\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{{x^3} - x_0^3}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\left( {x - {x_0}} \right)\left( {{x^2} + x{x_0} + x_0^2} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \left( {{x^2} + x{x_0} + x_0^2} \right) = 3x_0^2\)
Vậy hàm số \(y = {x^3}\) có đạo hàm là hàm số \(y' = 3{x^2}\)
b) \(y' = \left( {{x^n}} \right)' = n{x^{n - 1}}\)
Cho hàm số y = (2m + 1) x + n . Biết rằng đồ thị hàm số trùng với đường thẳng y = 3x - 2. Tính m + n?
A. -1
B. 0
C. 1
D. 2
Đáp án A
Để đồ thị hàm số y = (2m + 1)x + n trùng với đường thẳng y = 3x - 2 thì:
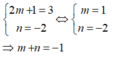
Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Biết rằng hàm số y=f(x) có m điểm cực trị, hàm số
y
=
f
(
x
)
có n điểm cực trị, hàm số
y
=
f
x
có p điểm cực trị. Giá trị m+n+p là 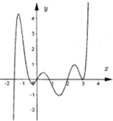
A. 26
B. 30
C. 27
D. 31
Cho hàm số y = mx + 1 x + n . Biết đồ thị hàm số có tiệm cận đứng là x = -1 và y'(0) = 2. Giá trị của m + n là
A. 2
B. 4
C. 1
D. 3
Tìm điều kiện của m, n để các hàm số sau là hàm số bậc nhất:
y= m(x+1)2+n(x-2)2
cho hàm số bậc nhất y(m-1)x+n ; y=(2m+4)x+2n -2 . tìm giá trị m , n để đồ thị của hai hàm đã cho là hai đường thẳng song song
Để hai đồ thị này song song thì
\(\left\{{}\begin{matrix}2m+4=m-1\\n< >2n-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=-5\\n< >2\end{matrix}\right.\)