Cho dãy số ( x n ) xác định bởi x 1 = 2 , x n + 1 = 2 + x n , n ∈ N. Mệnh đề nào là mệnh đề đúng ?
![]()
![]()
![]()
![]()
1) cho dãy số được xác định bởi
a) Tính
2) cho dãy số được xác định bởi
b) \(\dfrac{13}{7}\) là số hạng thứ mấy của dãy
a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = n^2 - 1:
u1 = 1^2 - 1 = 0 u2 = 2^2 - 1 = 3 u3 = 3^2 - 1 = 8 u4 = 4^2 - 1 = 15
Vậy u1 = 0, u2 = 3, u3 = 8, u4 = 15.
b) Để tìm số hạng thứ mấy trong dãy có giá trị 99, ta giải phương trình n^2 - 1 = 99:
n^2 - 1 = 99 n^2 = 100 n = 10 hoặc n = -10
Vì số hạng của dãy phải là số tự nhiên nên ta chọn n = 10. Vậy số hạng thứ mấy có giá trị 99 là u10.
a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = (2n - 1)/(n + 1):u1 = (21 - 1)/(1 + 1) = 1/2 u2 = (22 - 1)/(2 + 1) = 3/3 = 1 u3 = (23 - 1)/(3 + 1) = 5/4 u4 = (24 - 1)/(4 + 1) = 7/5
Vậy u1 = 1/2, u2 = 1, u3 = 5/4, u4 = 7/5.
b) Để tìm số hạng thứ mấy trong dãy có giá trị 137137, ta giải phương trình (2n - 1)/(n + 1) = 137137:
(2n - 1)/(n + 1) = 137137 2n - 1 = 137137(n + 1) 2n - 1 = 137137n + 137137 137135n = 137138 n = 1
Vậy số hạng thứ mấy có giá trị 137137 là u1.
Cho dãy số u n được xác định bởi u 1 = 2 u n + 1 = 4 u n + 9
Dãy số v n xác định bởi v n = u n + 3 , với mọi n ≥ 1 . Khẳng định nào dưới đây đúng?
A. Dãy v n là cấp số cộng với công sai d=3 .
B. Dãy v n là cấp số nhân với công bội q=4.
C. Dãy v n là cấp số cộng với công sai d=4 .
D. Dãy v n là cấp số nhân với công bội q= 9
1) cho dãy số \(\left(u_n\right)\) xác định bởi \(u_n=n^2-1\)
a) tính \(u_1,u_2,u_3,u_4\)
b) 99 là số hạng thứ mấy của dãy
2) cho dãy số \(\left(u_n\right)\) xác định bởi \(u_n=\dfrac{2n-1}{n+1}\)
a) tính \(u_1,u_2,u_3,u_4\)
b) \(\dfrac{13}{7}\) là số hạng thứ mấy của dãy
2:
a: \(u_1=\dfrac{2-1}{1+1}=\dfrac{1}{2}\)
\(u_2=\dfrac{2\cdot2-1}{2+1}=1\)
\(u_3=\dfrac{2\cdot3-1}{3+1}=\dfrac{5}{4}\)
\(u_4=\dfrac{2\cdot4-1}{4+1}=\dfrac{7}{5}\)
b: Đặt \(\dfrac{2n-1}{n+1}=\dfrac{13}{7}\)
=>7(2n-1)=13(n+1)
=>14n-7=13n+13
=>n=20
=>13/7 là số hạng thứ 20 trong dãy
1:
a: u1=1^2-1=0
u2=2^2-1=3
u3=3^2-1=8
u4=4^2-1=15
b: 99=n^2-1
=>n^2=100
mà n>=0
nên n=10
=>99 là số thứ 10 trong dãy
1) cho dãy số \(\left(u_n\right)\) xác định bởi \(u_n=n^2+1\)
a) tính \(u_1,u_2,u_3,u_4\)
b) 101 là số hạng thứ mấy của dãy
2) cho dãy số \(\left(u_n\right)\) xác định bởi \(u_n=\dfrac{n+1}{2n-1}\)
a) tính \(u_1,u_2,u_3,u_4\)
b) \(\dfrac{31}{59}\) là số hạng thứ mấy của dãy
1:
a:
u1=1^2+1=2
u2=2^2+1=5
u3=3^2+1=10
u4=4^2+1=17
b: Đặt 101=n^2+1
=>n^2=100
=>n=10
=>101 là số hạng thứ 10
2:
a: \(u1=\dfrac{1+1}{2-1}=2\)
\(u2=\dfrac{2+1}{2\cdot2-1}=\dfrac{3}{3}=1\)
\(u_3=\dfrac{3+1}{2\cdot3-1}=\dfrac{4}{5}\)
\(u_4=\dfrac{4+1}{2\cdot4-1}=\dfrac{5}{7}\)
b: Đặt \(\dfrac{n+1}{2n-1}=\dfrac{31}{59}\)
=>59(n+1)=31(2n-1)
=>62n-31=59n+59
=>3n=90
=>n=30
=>31/59 là số hạng thứ 30 trong dãy
Cho dãy số thực \(\left(u_n\right)\)xác định bởi: \(\left\{{}\begin{matrix}u_1=\sin1\\u_n=u_{n-1}+\dfrac{\sin n}{n^2},\forall n\in N,n\ge2\end{matrix}\right.\)
Chứng minh rằng dãy số xác định như trên là một dãy số bị chăn
Từ công thức truy hồi ta được:
\(u_n=sin1+\dfrac{sin2}{2^2}+\dfrac{sin3}{3^2}+...+\dfrac{sinn}{n^2}\)
\(\Rightarrow\left|u_n\right|=\left|sin1+\dfrac{sin2}{2^2}+...+\dfrac{sinn}{n^2}\right|\le\left|sin1\right|+\left|\dfrac{sin2}{2^2}\right|+...+\left|\dfrac{sinn}{n^2}\right|\)
\(\Rightarrow\left|u_n\right|< \left|1\right|+\left|\dfrac{1}{2^2}\right|+\left|\dfrac{1}{3^2}\right|+...+\left|\dfrac{1}{n^2}\right|=1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{n^2}\)
Lại có:
\(1+\dfrac{1}{2^2}+...+\dfrac{1}{n^2}< 1+\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{\left(n-1\right)n}=2-\dfrac{1}{n}< 2\)
\(\Rightarrow\left|u_n\right|< 2\Rightarrow u_n\) là dãy bị chặn
Cho dãy số (an) xác định bởi: a1=5; an= an-1 + 3n ∀ n ≥ 2. Chứng minh dãy số bn= an+1 - an ∀ n ≥ 2 là một cấp số cộng.
Cho dãy số (Un) xác định bởi công thức truy hồi: u 1 = - 2 u n = u n - 1 + 2 n , ∀ n ≥ 2 , n ∈ N * . Tìm số hạng tổng quát của dãy số
![]()
![]()
![]()
![]()
Cho dãy số (Un) được xác định bởi \(u_n=\dfrac{n^2+3n+7}{n+1}\). Dãy số có bao nhiêu số hạng nhận giá trị nguyên
Để \(u_n\) nguyên thì \(n^2+3n+7⋮n+1\)
=>\(n^2+n+2n+2+5⋮n+1\)
=>\(5⋮n+1\)
=>\(n+1\in\left\{1;-1;5;-5\right\}\)
=>\(n\in\left\{0;-2;4;-6\right\}\)
Vậy: \(u_n\) có 4 số hạng nhận giá trị nguyên
Cho dãy số u n được xác định bởi u 1 = 3 2 n + 1 u n + 1 = n u n + n + 2 . Tính lim u n .
A. lim u n = 1
B. lim u n = 4
C. lim u n = 3
D. lim u n = 0
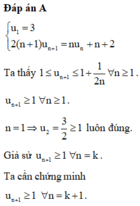
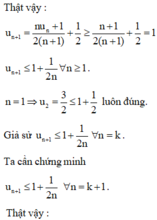
u n + 1 = n u n + 1 2 ( n + 1 ) + 1 2 ≤ n 1 + 1 2 n 2 ( n + 1 ) + 1 2 ≤ 1 + 1 4 ( n + 1 ) ≤ 1 + 1 2 n
suy ra lim u n = 1
Cho dãy số u n xác định bởi u 1 = 1 , u n + 1 = 1 3 2 u n + n - 1 n 2 + 3 n + 2 , n ∈ N * . Khi đó u 2018 bằng
A. 2 2016 3 2017 + 1 2019
B. 2 2018 3 2017 + 1 2019
C. 2 2017 3 2018 + 1 2019
D. 2 2017 3 2018 - 1 2019