Ta có 

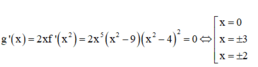
Bảng biến thiên của hàm số y= g( x)

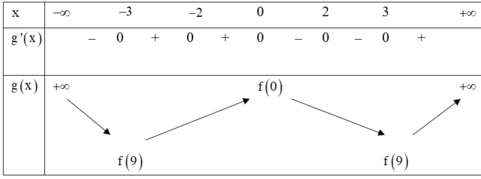
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng ( 3: + ∞)  hàm số nghịch biến trong khoảng (-∞; -3) .

Hàm số có 3 cực trị, hàm số đạt giá trị nhỏ nhất tại x= ±3

Vậy có 3 khẳng định đúng là khẳng định I, II, IV

Chọn C.

Hàm số ở câu a) \(y = 9{x^2} + 5x + 4\) là hàm số bậc hai với \(a = 9,b = 5,c = 4\)

Hàm số ở câu b), c) không phải là hàm số bậc hai vì chứa \({x^3}\)

Hàm số ở câu d) \(y = 5{x^2} + \sqrt x  + 2\) không phải là hàm số bậc hai vì chứa \(\sqrt x \)

Câu 5: C

Câu 7: A

5 là c

7 là a

1) \(f\left(x\right)=2x-5\)

\(f'\left(x\right)=2\)

\(\Rightarrow f'\left(4\right)=2\)

2) \(y=x^2-3\sqrt[]{x}+\dfrac{1}{x}\)

\(\Rightarrow y'=2x-\dfrac{3}{2\sqrt[]{x}}-\dfrac{1}{x^2}\)

3) \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt[]{x}\)

\(\Rightarrow f'\left(x\right)=\dfrac{1.\left(x+3\right)-1.\left(x+9\right)}{\left(x-3\right)^2}+\dfrac{4}{2\sqrt[]{x}}\)

\(\Rightarrow f'\left(x\right)=\dfrac{x+3-x-9}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)

\(\Rightarrow f'\left(x\right)=\dfrac{12}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)

\(\Rightarrow f'\left(x\right)=2\left[\dfrac{6}{\left(x-3\right)^2}+\dfrac{1}{\sqrt[]{x}}\right]\)

\(\Rightarrow f'\left(1\right)=2\left[\dfrac{6}{\left(1-3\right)^2}+\dfrac{1}{\sqrt[]{1}}\right]=2\left(\dfrac{3}{2}+1\right)=2.\dfrac{5}{2}=5\)

3:

\(\Delta=\left(2m-1\right)^2-4\left(-2m-11\right)\)

=4m^2-4m+1+8m+44

=4m^2+4m+45

=(2m+1)^2+44>=44>0

=>Phương trình luôn có hai nghiệm pb

|x1-x2|<=4

=>\(\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}< =4\)

=>\(\sqrt{\left(2m-1\right)^2-4\left(-2m-11\right)}< =4\)

=>\(\sqrt{4m^2-4m+1+8m+44}< =4\)

=>0<=4m^2+4m+45<=16

=>4m^2+4m+29<=0

=>(2m+1)^2+28<=0(vô lý)

\(a,f\left(1\right)=3\cdot1^2+1+1=5\\ f\left(-\dfrac{1}{3}\right)=3\cdot\left(-\dfrac{1}{3}\right)^2-\dfrac{1}{3}+1=\dfrac{1}{3}-\dfrac{1}{3}+1=1\\ f\left(\dfrac{2}{3}\right)=3\cdot\left(\dfrac{2}{3}\right)^2-\dfrac{2}{3}+1=\dfrac{4}{3}-\dfrac{2}{3}+1=\dfrac{5}{3}\\ f\left(-2\right)=3\cdot\left(-2\right)^2-2+1=11\\ f\left(-\dfrac{4}{3}\right)=3\cdot\left(-\dfrac{4}{3}\right)^2-\dfrac{4}{3}+1=\dfrac{16}{3}-\dfrac{4}{3}+1=5\)

\(b,f\left(\dfrac{2}{3}\right)=\left|2\cdot\dfrac{2}{3}-9\right|-3=\dfrac{23}{3}-3=\dfrac{14}{3}\\ f\left(-\dfrac{5}{4}\right)=\left|2\cdot\left(-\dfrac{5}{4}\right)-9\right|-3=\dfrac{23}{2}-3=\dfrac{17}{2}\\ f\left(-5\right)=\left|2\left(-5\right)-9\right|-3=19-3=16\\ f\left(4\right)=\left|2\cdot4-9\right|-3=1-3=-2\\ f\left(-\dfrac{3}{8}\right)=\left|2\cdot\left(-\dfrac{3}{8}\right)-9\right|-3=\dfrac{39}{4}-3=\dfrac{27}{4}\)

\(c,x=0\Rightarrow y=2\cdot0^2-7=-7\\ x=-3\Rightarrow y=2\cdot\left(-3\right)^2-7=11\\ x=-\dfrac{1}{2}\Rightarrow y=2\cdot\left(-\dfrac{1}{2}\right)^2-7=\dfrac{-13}{2}\\ x=\dfrac{2}{3}\Rightarrow y=2\cdot\left(\dfrac{2}{3}\right)^2-7=-\dfrac{55}{9}\)

Gọi `M(x,y)` là điểm thuộc TT.

`y'=3x^2+2x`

TT song song với `y=8x+9=> f'(x_0)=8`

`=> 3x_0^2+2x_0=8`

`<=>` \(\left[{}\begin{matrix}x_0=\dfrac{4}{3}\\x_0=-2\end{matrix}\right.\)

TH1: `x_0=4/3 => y_0 = 193/27`

`=>` PTTT: `y=8(x-4/3)+193/27=8x-96/27`

TH2: `x_0=-2 => y_0=-1`

`=>` PTTT: `y=8(x+2)-1=8x+15`

a: \(f\left(x\right)=\sqrt{x^2-6x+9}=\sqrt{\left(x-3\right)^2}=\left|x-3\right|\)

\(f\left(-1\right)=\left|-1-3\right|=4\)

\(f\left(5\right)=\left|5-3\right|=\left|2\right|=2\)

b: f(x)=10

=>\(\left[{}\begin{matrix}x-3=10\\x-3=-10\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=13\\x=-7\end{matrix}\right.\)

c: \(A=\dfrac{f\left(x\right)}{x^2-9}=\dfrac{\left|x-3\right|}{\left(x-3\right)\left(x+3\right)}\)

TH1: x<3 và x<>-3

=>\(A=\dfrac{-\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{-1}{x+3}\)

TH2: x>3

\(A=\dfrac{\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{1}{x+3}\)