Tìm giá trị của tham số m để hàm số
y = (m - 1) x 4 - m x 2 + 3 có đúng một cực trị
Câu 1: Tìm giá trị thực của tham số m để hàm số
y= \(\dfrac{1}{3}x^3-mx^{2^{ }}+\left(m^2-4\right)x+3\) tại x=3
Câu 2:Tìm m để hàm số \(y=x^3-2mx^2+mx+1\) đạt cực tiểu tại x=1
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị
Tìm giá trị của tham số m để hàm số
y = (m - 1) x 4 - m x 2 + 3 có đúng một cực trị
y' = 4(m - 1) x 3 - 2mx = 2x[2(m - 1) x 2 - m]
Hàm số có đúng một cực trị khi y' = 0 có đúng một nghiệm, tức là
2x[2(m - 1) x 2 - m] = 0 chỉ có nghiệm x = 0
Muốn vậy, phải có m = 1 hoặc 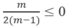
⇒ 0 ≤ m ≤ 1.
Vậy với 0 ≤ m ≤ 1 hàm số đã cho có một cực trị duy nhất.
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = x 2 ( x + 1 ) ( x 2 + 2 m x + 4 ) . Có bao nhiêu giá trị nguyên âm của tham số m để hàm số y = f ( x ) 2 có đúng một điểm cực trị.
A. 1.
B. 4.
C. 2.
D. 3.
Tìm tất cả các giá trị của tham số \(m\) để hàm số \(y=x^4+4mx^3+3\left(m+1\right)x^2+1\) có cực tiểu mà không có cực đại
\(y'=4x^3+12mx^2+6\left(m+1\right)x=2x\left[2x^2+6mx+3\left(m+1\right)\right]\)
Hàm có cực tiểu mà ko có cực đại khi và chỉ khi \(y'=0\) có đúng 1 nghiệm đơn
TH1: \(2x^2+6mx+3\left(m+1\right)=0\) có nghiệm \(x=0\)
\(\Leftrightarrow m=-1\)
TH2: \(2x^2+6mx+3\left(m+1\right)=0\) có ít hơn 2 nghiệm
\(\Leftrightarrow\Delta'=9m^2-6\left(m+1\right)\le0\)
\(\Leftrightarrow\dfrac{1-\sqrt{7}}{3}\le m\le\dfrac{1+\sqrt{7}}{3}\)
Bài 4: Tìm giá trị của tham số m để hàm số: a) y=mx3 +mx2 −x+1 có cực đại, cực tiểu. b) y=x4 +(m−1)x2+1 có 3 cực trị.
Cho hàm số f(x) = (m - 1)x3 - 5x2 + (m+3)x + 3. Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y = f(\(\left|x\right|\)) có đúng 3 điểm cực trị?
- Với \(m=1\) thỏa mãn
- Với \(m\ne1\):
\(f'\left(x\right)=3\left(m-1\right)x^2-10x+m+3\)
\(f\left(\left|x\right|\right)\) có số cực trị bằng \(2k+1\) với \(k\) là số cực trị dương của \(f\left(x\right)\) nên hàm có 3 cực trị khi \(f'\left(x\right)=0\) có đúng 1 nghiệm dương
TH1: \(f'\left(x\right)=0\) có 1 nghiệm bằng 0 \(\Rightarrow m=-3\Rightarrow f'\left(x\right)=-12x^2-10x\) ko có nghiệm dương (loại)
TH2: \(f'\left(x\right)=0\) ko có nghiệm bằng 0 nào \(\Rightarrow f'\left(x\right)=0\) khi và chỉ khi nó có 2 nghiệm trái dấu
\(\Rightarrow ac< 0\Leftrightarrow3\left(m-1\right)\left(m+3\right)< 0\)
\(\Rightarrow-3< m< 1\)
Vậy \(-3< m\le1\)
Tìm các giá trị của tham số m để hàm số y = m x 4 + ( m - 1 ) x 2 + m chỉ có đúng một cực trị
A. 0 < m ≤ 1 .
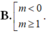
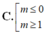
D. 0 ≤ m ≤ 1 .
Chọn C
Trường hợp 1: m = 0
Ta có hàm số: y = - x 2 , hàm số này có 1 cực trị.
Vậy m = 0 thỏa mãn.
Trường hợp 2: m ≠ 0
y ' = 4 m x 3 + 2 ( m - 1 ) x
Hàm số có đúng 1 cực trị.
![]()
Kết hợp TH1 và TH2
![]()