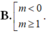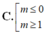y' = 4(m - 1) x 3 - 2mx = 2x[2(m - 1) x 2 - m]
Hàm số có đúng một cực trị khi y' = 0 có đúng một nghiệm, tức là
2x[2(m - 1) x 2 - m] = 0 chỉ có nghiệm x = 0
Muốn vậy, phải có m = 1 hoặc 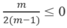
⇒ 0 ≤ m ≤ 1.
Vậy với 0 ≤ m ≤ 1 hàm số đã cho có một cực trị duy nhất.