Ta có: \(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\)

Vì CD là phân giác trong góc C 

\(\Rightarrow\dfrac{AD}{BD}=\dfrac{AC}{BC}\Rightarrow\dfrac{AD}{BD}=\dfrac{8}{10}=\dfrac{4}{5}\Rightarrow BD=\dfrac{5}{4}AD\)

Ta có: \(AD+BD=AB\Rightarrow AD+\dfrac{5}{4}AD=6\Rightarrow\dfrac{9}{4}AD=6\Rightarrow AD=\dfrac{8}{3}\)

Vì CD,CE lần lượt là phân giác trong và ngoài góc C

\(\Rightarrow CD\bot CE\Rightarrow\Delta DCE\) vuông tại C có \(AC\bot DE\)

\(\Rightarrow AD.AE=AC^2\Rightarrow AE=\dfrac{AC^2}{AD}=\dfrac{8^2}{\dfrac{8}{3}}=24\)

Bài 1. Em hãy chọn trong các phương án dưới đây để được một phát biểu đúng.

Qua hai điểm A và B phân biệt có

(A) vô số đường thẳng                                (B) Chỉ có 1 đường thẳng

(C) không có đường thẳng nào

Đáp án: B

Bài 2. Vẽ hình cho các trường hợp sau:

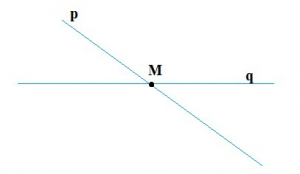
a) Hai đường thẳng p và q cắt nhau tại điểm M

b) Đường thẳng a cắt hai đường thẳng m và n theo thứ tự tại X và Y trong hai trường hợp m và n cắt nhau, hoặc m và n song song với nhau

a)

Dính chùm😤

a) Xét ΔCBA vuông tại B có

\(\tan\widehat{ACB}=\frac{AB}{BC}=\frac{6}{8}=\frac{3}{4}\)

\(\Rightarrow\widehat{ACB}\simeq36^052'\)

Vậy: \(\widehat{ACB}\simeq36^052'\)

b)

Áp dụng định lí Pytago vào ΔCBA vuông tại B, ta được:

\(AC^2=BA^2+BC^2\)

\(\Leftrightarrow AC^2=6^2+8^2=100\)

hay \(AC=\sqrt{100}=10\)

Xét ΔCBA có AD là tia phân giác của \(\widehat{BAC}\)(gt)

nên \(\frac{AB}{BD}=\frac{AC}{CD}\)(Tính chất đường phân giác của tam giác)

hay \(\frac{6}{BD}=\frac{10}{CD}\)

Ta có: BD+CD=BC(D nằm giữa B và C)

hay BD+CD=8

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\frac{6}{BD}=\frac{10}{CD}=\frac{6+10}{BD+CD}=\frac{16}{8}=2\)

\(\Leftrightarrow BD=\frac{6}{2}=3\)

Xét ΔABD vuông tại B có

\(\tan\widehat{ADB}=\frac{AB}{BD}=\frac{6}{3}=2\)

a: \(BC=\sqrt{8^2+15^2}=17\left(cm\right)\)

\(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{120}{17}\left(cm\right)\)

b: Xét ΔAHB vuông tại H có HM là đường cao

nên \(AM\cdot AB=AH^2\left(1\right)\)

Xét ΔAHC vuông tại H có HN là đường cao

nên \(AN\cdot AC=AH^2\left(2\right)\)

Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)

Bạn tự vẽ hình nha :

a, Tứ giác AMHN có : \(\widehat{A}=\widehat{M}=\widehat{N}=90^o\)

\(\Rightarrow\) Tứ giác AMHN là hình chữ nhật

b, \(\Delta ABC:\)    \(\widehat{A}=90^o\)

\(\Rightarrow\) \(BC^2=AB^2+AC^2\)  ( Định lý Py - ta - go )

hay  \(BC^2=8^2+15^2=289\)

\(\Rightarrow\) BC = 17 ( cm )

Xét  \(\Delta AHB\) và  \(\Delta CAB\) có :

\(\widehat{AHB}=\widehat{CAB}=90^o\)

\(\widehat{B}:chung\)

\(\Rightarrow\) \(\Delta AHB\) đồng dạng  \(\Delta CAB\left(g.g\right)\)

\(\Rightarrow\) \(\frac{AH}{AB}=\frac{AC}{BC}\)          \(\Rightarrow\) \(AH=\frac{AB.AC}{BC}=\frac{8.15}{17}=\frac{120}{17}\left(cm\right)\)

Mà AMHN là hình chữ nhật

=> \(MN=AH=\frac{120}{17}\left(cm\right)\)

c, Xét \(\Delta AMH\) và \(\Delta AHB\) có :

\(\widehat{A}:chung\)

\(\widehat{AMH}=\widehat{AHB}=90^o\)

\(\Rightarrow\) \(\Delta AMH\) đồng dạng \(\Delta AHB\left(g.g\right)\)

\(\Rightarrow\) \(\frac{AM}{AH}=\frac{AH}{AB}\)       \(\Rightarrow\) \(AM.AB=AH^2\) ( 1 )

Tương tự :  \(\Delta ANH\) đồng dạng \(\Delta AHC\left(g.g\right)\)

\(\Rightarrow\) \(\frac{AN}{AH}=\frac{AH}{AC}\)    \(\Rightarrow\) \(AN.AC=AH^2\)    ( 2 )

Từ ( 1 ) và ( 2 )      => đpcm

a: Xét tứ giác ACBD có 

M là trung điểm của AB

M là trung điểm của CD

Do đó: ACBD là hình bình hành

b: Xét ΔABC có 

N là trung điểm của BC

P là trung điểm của AC

Do đó: NP là đường trung bình

=>NP=AB/2 và NP//AB

Xét tứ giác ABNQ có 

NQ//AB

AQ//BN

Do đó: ABNQ là hình bình hành

Suy ra: NQ=AB

=>NQ=2NP

=>P là trung điểm của NQ

Xét tứ giác ANCQ có

P là trung điểm của AC

P là trung điểm của NQ

Do đó: ANCQ là hình bình hành

mà NA=NC

nên ANCQ là hình thoi