cho tam giác abc vuông tại a có ab=12cm,ac=16cm.vẽ đường cao ah chứng minh Δhba Δabc

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A,vẽ đường cao AH.ChoAB=6cm;AC=8cm
a/ Chứng minh ΔHBA đồng dạng ΔABC
b/ Tính BC,AH,BH
a.
Xét hai tam giác vuông HBA và ABC có:
\(\left\{{}\begin{matrix}\widehat{HBA}\text{ chung}\\\widehat{AHB}=\widehat{BAC}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta HBA\sim\Delta ABC\left(g.g\right)\)
b.
Áp dụng định lý Pitago:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Do \(\Delta HBA\sim\Delta ABC\left(cmt\right)\Rightarrow\dfrac{AH}{AC}=\dfrac{AB}{BC}\)
\(\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{6.8}{10}=4,8\left(cm\right)\)
Áp dụng định lý Pitago trong tam giác vuông HBA:
\(BH=\sqrt{AB^2-AH^2}=\sqrt{6^2-4,8^2}=3,6\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB=12cm,AC=16cm.Vẽ đường cao AH
a)Chứng minh tam giác HBA đồng dạng với tam giác ABC
b)Tính BC,AH,BH.
c)Vẽ đường phân giác AD của tam giác ABC(D thuộc BC).Tính BD,CD
d)Trên Ah lấy điểm K sao cho AK=3.6cm.Từ K kẻ đường thẳng song song BC cắt AB và AC lần lượt tại M và N.Tính diện tích tứu giác BMNC
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
Do đó:ΔHBA\(\sim\)ΔABC
b: \(BC=\sqrt{AB^2+AC^2}=20\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=9.6\left(cm\right)\)
\(BH=\dfrac{AB^2}{BC}=\dfrac{12^2}{20}=7.2\left(cm\right)\)
c: Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/3=CD/4
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{20}{7}\)
Do đó; BD=60/7(cm); CD=80/7(cm)
Đúng 1
Bình luận (0)
Cho TAm Giác ABC vuông tại A , AB =6cm , AC = 8cm .Đường cao AH
a) Chứng minh ΔABC∞ΔHBA
b) Tính cạnh BC và AH
c) Tính tỉ số diện tích của ΔHAB và ΔHAC
d) Đường phân giác AD .TÍnh BD,CD và tỉ số diện tích của ΔABC và ΔACD
a, Xét ΔABC và ΔHBA có:
∠BAC chung, ∠BHA=∠BAC (=90o)
=> ΔABC ∼ ΔHBA (g.g)
b, Áp dụng đ/l Pitago vào △ABC ta có:
BC2=AB2+AC2 => BC=√(62+82)=10 (cm)
Ta có: SABC=\(\dfrac{1}{2}\)AB.AC=\(\dfrac{1}{2}\)AH.BC
=> 6.8=AH.10 => AH=4,8 (cm)
c, Xét △HAB và △HCA có:
∠BHA=∠CHA (=90o), ∠ABC=∠HAC (cùng phụ ∠BCA)
=> △HAB ∼ △HCA (g.g)
=> \(\dfrac{AB}{AC}=\dfrac{\text{△HAB}}{\text{△HCA}}\)=\(\dfrac{6}{8}\)=\(\dfrac{3}{4}\)
d, AD là đường p/g của △ABC => \(\dfrac{AB}{BD}=\dfrac{AC}{DC}\)=\(\dfrac{AB+AC}{BD+DC}=\dfrac{14}{10}=\dfrac{7}{5}\)
=> \(\dfrac{AB}{BD}=\dfrac{7}{5}\) => \(\dfrac{6}{BD}=\dfrac{7}{5}\) => BD=\(\dfrac{30}{7}\) (cm)
=> \(\dfrac{AC}{DC}\)\(=\dfrac{7}{5}\) => \(\dfrac{8}{DC}=\dfrac{7}{5}\) => DC=\(\dfrac{40}{7}\) (cm)
Đúng 1
Bình luận (0)
Cho TAm Giác ABC vuông tại A , AB =6cm , AC = 8cm .Đường cao AH
a) Chứng minh ΔABC∞ΔHBA
b) Tính cạnh BC và AH
c) Tính tỉ số diện tích của ΔHAB và ΔHAC
d) Đường phân giác AD .TÍnh BD,CD và tỉ số diện tích của ΔABC và ΔACD
Cho ΔABC vuông tại A ( AB < AC ), đường cao AH ( H ϵ BC ).
1. Chứng minh: ΔHBA đồng dạng ΔABC và BA.BA=BH.BC.
2. Kẻ phân giác BE của góc ABC ( E ϵ AC ) , BE cát AH tại I .
Chứng minh : ΔHBI đồng dạng ΔABE .
3. Chứng minh : AI=AE
1.Xét ΔHBA và ΔABC có:
góc AHB=góc BAC=90o
Góc B chung
=> ΔABC đồng dạng ΔHBA (g.g)
=>\(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)\(\Rightarrow BA.BA=BH.BC\)
2. Xét ΔHBI và ΔABE có:
góc ABE=IBH (Vì BE là tia phân giác của góc B, I nằm trên BE)
góc BAE=góc IHB=90o
=>ΔHBI đồng dạng ΔABE (g.g)
Đúng 1
Bình luận (1)
Cho ΔABC vuông tại A (AB<AC), đường cao AH (H∈BC). BD là phân giác của ∠ABC (D∈AC). Gọi I là giao điểm của AH và BD.
a. Chứng minh: ΔHBA đồng dạng ΔABC và ΔHBI đồng dạng ΔABD
b. Chứng minh: \(\frac{IA}{IH}=\frac{BC}{AB}\)
c. Đường thẳng vuông góc với BD tại B cắt đường thẳng AH tại M. CHứng minh: MA.IH = MH.IA
Giúp mình ý b,c với ạ
Cho tam giác ABC vuông tại A có AH là đường cao.
V
ẽ
H
D
⊥
A
B
(
D
∈
A
B
)
.
H
E
⊥
A
C
(
E
∈
A
C
)
.
A...
Đọc tiếp
Cho tam giác ABC vuông tại A có AH là đường cao. V ẽ H D ⊥ A B ( D ∈ A B ) . H E ⊥ A C ( E ∈ A C ) . A B = 12 c m , A C = 16 c m
a) Chứng minh : Δ H A C ~ Δ A B C
b) Chứng minh : A H 2 = A D . A B
c) Chứng minh : A D . A B = A E . A C .

a) Xét ΔHAC và ΔABC có:
∠(ACH ) là góc chung
∠(BAC)= ∠(AHC) = 90o
⇒ ΔHAC ∼ ΔABC (g.g)
b) Xét ΔHAD và ΔBAH có:
∠(DAH ) là góc chung
∠(ADH) = ∠(AHB) = 90o
⇒ ΔHAD ∼ ΔBAH (g.g)
![]()
c) Tứ giác ADHE có 3 góc vuông ⇒ ADHE là hình chữ nhật.
⇒ ΔADH= ΔAEH ( c.c.c) ⇒ ∠(DHA)= ∠(DEA)
Mặt khác: ΔHAD ∼ ΔBAH ⇒ ∠(DHA)= ∠(BAH)
∠(DEA)= ∠(BAH)
Xét ΔEAD và ΔBAC có:
∠(DEA)= ∠(BAH)
∠(DAE ) là góc chung
ΔEAD ∼ ΔBAC (g.g)

d) ΔEAD ∼ ΔBAC

ΔABC vuông tại A, theo định lí Pytago:

Theo b, ta có:
![]()


Đúng 2
Bình luận (0)
Cho ΔABC vuông tại A (ABAC), đường cao AH.a)Chứng minh ΔABC đồng dạng ΔHBA từ đó suy ra AB2BC.BH; AB.ACBC.AH.b)Chứng minh ΔABC đồng dạng ΔHAC từ đó suy ra AC2BC.CH.c)Tia phân giác của góc ABC cắt AH tại K, cắt AC tại I. Chứng minh: ΔABK đồng dạng ΔCBI.d)Chứng minhdfrac{AI}{IC}dfrac{KH}{AK}e)Tính tỉ số diện tích của ΔBHK và ΔBAI khi AB3cm, AC4cm.f)Tính diện tích ΔBIC
Đọc tiếp
Cho ΔABC vuông tại A (AB<AC), đường cao AH.
a)Chứng minh ΔABC đồng dạng ΔHBA từ đó suy ra AB2=BC.BH; AB.AC=BC.AH.
b)Chứng minh ΔABC đồng dạng ΔHAC từ đó suy ra AC2=BC.CH.
c)Tia phân giác của góc ABC cắt AH tại K, cắt AC tại I. Chứng minh: ΔABK đồng dạng ΔCBI.
d)Chứng minh\(\dfrac{AI}{IC}=\dfrac{KH}{AK}\)
e)Tính tỉ số diện tích của ΔBHK và ΔBAI khi AB=3cm, AC=4cm.
f)Tính diện tích ΔBIC
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng vơi ΔHBA
=>AC/HA=AB/HB=BC/AB
=>AB^2=BH*BC; AC*AB=AH*BC
b: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc C chung
=>ΔABC đồng dạngvới ΔHAC
=>CA/CH=CB/CA
=>CA^2=CH*CB
d: AI/IC=AB/BC
KH/AH=BH/BA
mà AB/BC=BH/BA
nên AI/IC=KH/AH
Đúng 1
Bình luận (0)
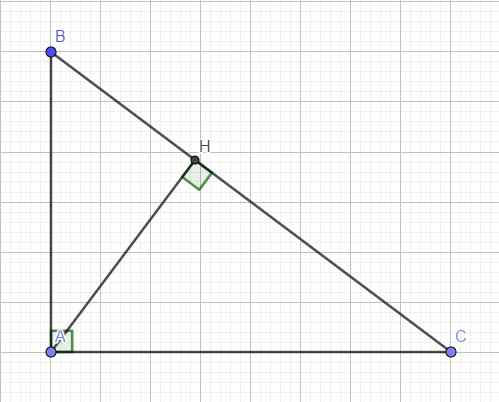
1.Cho tam giác ABC vuông tại A, có AB = 15cm, AC = 20cm. Vẽ đường cao AH (H∈BC).
a/ Chứng minh rằng ΔHBA ~ ΔABC.
b/ Chứng minh rằng AC² = BC.HC
c/ Tính độ dài các đoạn thẳng BC, HC.
a)Xét tam giác HAB và tam giác ABC
góc ABC : chung
góc BHA=góc BAC=90o
Suy ra: tam giác HAB ~ tam giác ABC (g-g)
b)Ta có: tam giác ABC vuông tại A
=>AC2=BC.HC (hệ thức lượng)
c)Ta có: \(BC^2=AB^2+AC^2=15^2+20^2=625\Rightarrow BC=25\left(cm\right)\)
Ta lại có: \(AC^2=BC.HC\left(HTL\right)\Rightarrow HC=\frac{AC^2}{BC}=\frac{20^2}{25}=16\left(cm\right)\)
Đúng 0
Bình luận (0)

a) Xét ΔHBA và ΔABC có:
∠BHA = ∠BAC = 900 ( GT)
Góc B: Chung
Vậy ΔHBA ~ ΔABC (g.g)
b) Xét ΔHAC và ΔABC.có:
∠AHC = ∠BAC =900 ( GT)
Góc C : Chung
Vậy ΔHAC ~ ΔABC (g.g)
Suy ra:
![]()
c) Áp dụng định lí Pytago cho vuông tại A, ta có:
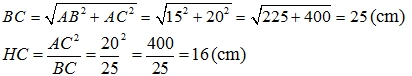
Đúng 0
Bình luận (0)
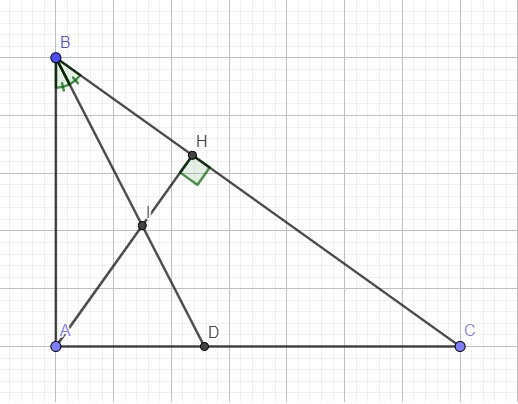
Cho tam giác ABC vuông tại A có đường cao AH (H ϵ BC) cắt đường phân giác BD tại I . Chứng minh rằng
a; ΔABC đồng dạng với ΔHBA
b; HI / IA = AD / DC
em cần gấp ai giúp em với
a.
Xét hai tam giác vuông ABC và HBA có:
\(\left\{{}\begin{matrix}\widehat{HBA}\text{ chung}\\\widehat{BAC}=\widehat{BHA}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta ABC\sim\Delta HBA\left(g.g\right)\)
b.
Do BD là phân giác góc B, áp dụng định lý phân giác cho tam giác ABC:
\(\dfrac{AD}{DC}=\dfrac{AB}{BC}\) (1)
Do BI là phân giác góc B, áp dụng định lý phân giác cho tam giác ABH:
\(\dfrac{HI}{AI}=\dfrac{BH}{AB}\) (2)
Mặt khác, từ câu a do \(\Delta ABC\sim\Delta HBA\Rightarrow\dfrac{AB}{BH}=\dfrac{BC}{BA}\Rightarrow\dfrac{AB}{BC}=\dfrac{BH}{AB}\) (3)
(1);(2);(3) \(\Rightarrow\dfrac{HI}{IA}=\dfrac{AD}{DC}\)
Đúng 1
Bình luận (0)