BT5; Lớp 7B trồng được 184 cây . Tìm số cây mỗi tổ trồng, biết rằng tổ 1 có 10 bạn ,tổ 2 có 11 bạn , tổ 3 có 12 bạn,tổ 4 có 13 bạn và số cây của bốn tổ trồng tỉ lệ với số học sinh của mỗi tổ
BT5. Make conditional sentences type 2 from the clues.
1. If / i / be / you / , i / plant / vegetables / garden.
_______________________________________
2. More / tourist / come / here / if / beach / be / cleaner .
________________________________________
3. What / happen / if / there / be / no / car / world ?
__________________________________________
Giups tui vs nha . ![]()
1: If I were you, I would plant many vegetables in the garden
2: More tourists will come here if the beach is cleaner
3: What would happen if there were no cars in the world?
BT5 Chứng minh:
1) \(\dfrac{1}{2}< \dfrac{1}{101}+\dfrac{1}{102}+...+\dfrac{1}{999}+\dfrac{1}{200}< 1\)
\(Tacó\)
\(\dfrac{1}{101}>\dfrac{1}{200}\)
\(\dfrac{1}{102}>\dfrac{1}{200}\)
...
\(\dfrac{1}{999}>\dfrac{1}{200}\)
Do đó :\(\dfrac{1}{101}+\dfrac{1}{102}+...+\dfrac{1}{999}+\dfrac{1}{200}>\dfrac{1}{200}+...+\dfrac{1}{200}=100.\dfrac{1}{200}=\dfrac{100}{200}=\dfrac{1}{2}\)
Ta lại có:
\(\dfrac{1}{102}< \dfrac{1}{101}\)
\(\dfrac{1}{103}< \dfrac{1}{101}\)
...
\(\dfrac{1}{200}< \dfrac{1}{101}\)
Do đó : \(\dfrac{1}{101}+\dfrac{1}{102}+\dfrac{1}{103}+...+\dfrac{1}{200}< \dfrac{1}{101}+\dfrac{1}{101}+...+\dfrac{1}{101}=\dfrac{1}{101}.100=\dfrac{100}{101}< 1\)Vậy ...( theo tớ , cậu nên đánh dấu (1) và (2) rồi suy ra ) .. khẳng định trên , học tốt
BT5: Thu gọn, chỉ ra phần hệ số và tìm bậc của các đơn thức sau:
\(a,\dfrac{1}{4}.\left(x^2y^3\right)^2.\left(-2xy\right)\)
\(\dfrac{1}{4}.\left(x^2y^3\right)^2.\left(-2xy\right)\\ =\dfrac{1}{4}.x^4y^6.\left(-2xy\right)\\ =\left[\dfrac{1}{4}.\left(-2\right)\right].\left(x^4.x\right)\left(y^6.y\right)\\ =-\dfrac{1}{2}x^5y^7\)
Hệ số : `-1/2`
Bậc : `12`
\(a,\dfrac{1}{4}.\left(x^2y^3\right)^2.\left(-2xy\right)\\
=\dfrac{1}{4}.\left(-2\right).x^4.y^6.x.y\\
=-\dfrac{1}{2}x^5y^7\)
hệ số \(:-\dfrac{1}{2}\)
Bậc của đơn thức : \(12\)
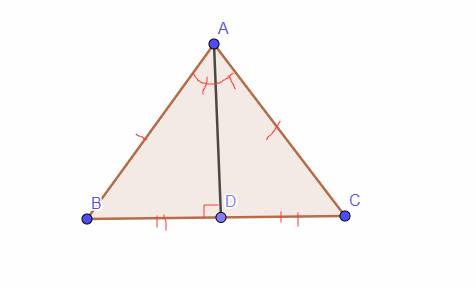
BT5: Cho ΔABC có AB = AC. Gọi D là trung điểm của BC. Chứng minh rằng:
a)ΔABD = ΔADC
b) AD là tia phân giác của BAC^
c) AD ⊥ BC
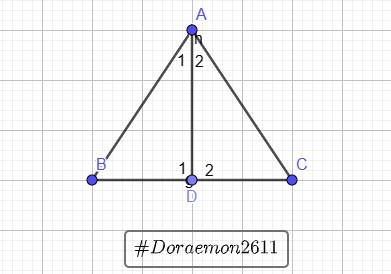
`a)` Vì `D` là trung điểm `BC=>DB=DC`
Xét `\triangle ABD` và `\triangle ACD` có:
`{:(AB=AC),(AD\text{ là cạnh chung}),(BD=CD):}}=>\triangle ABD=\triangle ACD` (c-c-c)
`b)` Vì `D` là tđ của `BC=>AD` là đường trung tuyến trong `\triangle ABC` cân tại `A`
`=>AD` đồng thời là đường phân giác của `\triangle ABC`
`=>AD` là tia phân giác của `\hat{BAC}`
`c)` Vì `D` là tđ của `BC=>AD` là đường trung tuyến trong `\triangle ABC` cân tại `A`
`=>AD` đồng thời là đường cao của `\triangle ABC`
`=>AD \bot BC`
`a,` Xét Tam giác `ABD` và Tam giác `ACD` có (bạn lưu ý ghi đúng tên của Tam giác để có các cạnh và góc tương ứng nhé)
`AB = AC (g``t)`
AD chung
`DB = DC (g``t)`
`=>` Tam giác `ABD =` Tam giác `ACD (c-c-c)`
`b,` Vì Tam giác `ABD =` Tam giác `ACD (a)`
`=>` \(\widehat{BAD}=\widehat{CAD}\) (2 góc tương ứng)
`=> AD` là tia phân giác của \(\widehat{BAC}\)
`c,` Vì Tam giác `ABD =` Tam giác `ACD (a)`
`=>` \(\widehat{ADB}=\widehat{ADC}\) (2 góc tương ứng)
Mà 2 góc này ở vị trí kề bù
`=>`\(\widehat{ADB}+\widehat{ADC}=180^0\)
`=>` \(\widehat{ADB}=\widehat{ADC}=\) \(\dfrac{180}{2}=90^0\)
`=>`\(AD\perp BC\) `(đpcm)`
BT5: Chứng minh rằng:
\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{100^2}< 1\)
Đặt:
\(A=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+.....+\dfrac{1}{100^2}\)
\(A< \dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+.....+\dfrac{1}{99.100}\)
\(A< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+.....+\dfrac{1}{99}-\dfrac{1}{100}\)
\(A< 1-\dfrac{1}{100}\)
\(A< 1\rightarrowđpcm\)
BT5: Cho hai đa thức \(C=x-\left[b-\left(c-a-b\right)\right]\)và\(D=b+\left[a-\left(c-b-a\right)\right]\)
Tính C+D và C-D
Sao ở đa thức C có x vậy, đề cho x hay sao thế?
\(C=x-\left[b-\left(c-a-b\right)\right]=x-\left(b-c+a+b\right)=x-b+c-a-b\)
\(=x-2b+c-a\)
\(D=b+\left[a-\left(c-b-a\right)\right]=b+\left(a-c+b+a\right)=b+a-c+b+a\)
\(=2a+2b-c\)
\(C+D=x-2b+c-a+2a+2b-c\)
\(=x+\left(-a+2a\right)+\left(-2b+2b\right)+\left(c-c\right)\)
\(=x+a\)
\(C-D=\left(x-2b+c-a\right)-\left(2a+2b-c\right)\)
\(=x-2b+c-a-2a-2b+c\)
\(=x+\left(-a-2a\right)+\left(-2b-2b\right)+\left(c+c\right)\)
\(=x-3a-4b+2c\)
BT5 : Chứng minh
2) \(\dfrac{3}{5}< \dfrac{1}{31}+\dfrac{1}{32}+\dfrac{1}{33}+....+\dfrac{1}{59}+\dfrac{1}{60}< \dfrac{4}{5}\)
Giải:
Đặt \(A=\dfrac{1}{31}+\dfrac{1}{32}+\dfrac{1}{33}+...+\dfrac{1}{59}+\dfrac{1}{60}\)
Ta có:
\(A=\dfrac{1}{31}+\dfrac{1}{32}+\dfrac{1}{33}+...+\dfrac{1}{59}+\dfrac{1}{60}\)
\(\Rightarrow A=\left(\dfrac{1}{31}+\dfrac{1}{32}+...+\dfrac{1}{40}\right)+\left(\dfrac{1}{41}+\dfrac{1}{42}+...+\dfrac{1}{50}\right)+\left(\dfrac{1}{51}+\dfrac{1}{52}+...+\dfrac{1}{60}\right)\)
Nhận xét:
\(\dfrac{1}{31}+\dfrac{1}{32}+...+\dfrac{1}{40}< \dfrac{1}{30}+\dfrac{1}{30}+...+\dfrac{1}{30}=\dfrac{1}{3}\)
\(\dfrac{1}{41}+\dfrac{1}{42}+...+\dfrac{1}{50}< \dfrac{1}{40}+\dfrac{1}{40}+...+\dfrac{1}{40}=\dfrac{1}{4}\)
\(\dfrac{1}{51}+\dfrac{1}{52}+...+\dfrac{1}{60}< \dfrac{1}{50}+\dfrac{1}{50}+...+\dfrac{1}{50}=\dfrac{1}{5}\)
\(\Rightarrow A< \dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}=\dfrac{47}{60}< \dfrac{48}{60}=\dfrac{4}{5}\)
\(\Rightarrow A< \dfrac{4}{5}\left(1\right)\)
Lại có:
\(\dfrac{1}{31}+\dfrac{1}{32}+...+\dfrac{1}{40}>\dfrac{1}{40}+\dfrac{1}{40}+...+\dfrac{1}{40}=\dfrac{1}{4}\)
\(\dfrac{1}{41}+\dfrac{1}{42}+...+\dfrac{1}{50}>\dfrac{1}{50}+\dfrac{1}{50}+...+\dfrac{1}{50}=\dfrac{1}{5}\)
\(\dfrac{1}{51}+\dfrac{1}{52}+...+\dfrac{1}{60}>\dfrac{1}{60}+\dfrac{1}{60}+...+\dfrac{1}{60}=\dfrac{1}{6}\)
\(\Rightarrow A>\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}=\dfrac{37}{60}>\dfrac{36}{60}=\dfrac{3}{5}\)
\(\Rightarrow A>\dfrac{3}{5}\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\)
\(\Rightarrow\dfrac{3}{5}< A< \dfrac{4}{5}\)
Vậy \(\dfrac{3}{5}< \dfrac{1}{31}+\dfrac{1}{32}+\dfrac{1}{33}+...+\dfrac{1}{59}+\dfrac{1}{60}< \dfrac{4}{5}\) (Đpcm)
Đặt A=131+132+133+...+159+160A=131+132+133+...+159+160
Ta có:
A=131+132+133+...+159+160A=131+132+133+...+159+160
⇒A=(131+132+...+140)+(141+142+...+150)+(151+152+...+160)⇒A=(131+132+...+140)+(141+142+...+150)+(151+152+...+160)
Nhận xét:
131+132+...+140<130+130+...+130=13131+132+...+140<130+130+...+130=13
141+142+...+150<140+140+...+140=14141+142+...+150<140+140+...+140=14
151+152+...+160<150+150+...+150=15151+152+...+160<150+150+...+150=15
⇒A<13+14+15=4760<4860=45⇒A<13+14+15=4760<4860=45
⇒A<45(1)⇒A<45(1)
Lại có:
131+132+...+140>140+140+...+140=14131+132+...+140>140+140+...+140=14
141+142+...+150>150+150+...+150=15141+142+...+150>150+150+...+150=15
151+152+...+160>160+160+...+160=16151+152+...+160>160+160+...+160=16
⇒A>14+15+16=3760>3660=35⇒A>14+15+16=3760>3660=35
⇒A>35(2)⇒A>35(2)
Từ (1)(1) và (2)(2)
⇒35<A<45⇒35<A<45
Vậy 35<131+132+133+...+159+160<4535<131+132+133+...+159+160<45
BT5: Nguyên tố R tạo thành hợp chất khí với hidro có CTHH chung là RH4. Trong đó hợp chất oxit cao nhất có 72,73% là oxi. a) Hãy xác định tên của nguyên tố R. b) Viết CTHH của hợp chất của R với Oxi và hidro.
a) CTHH oxit cao nhất là RO2
Có \(\dfrac{16.2}{M_R+16.2}.100\%=72,73\%=>M_R=12\left(g/mol\right)\)
=> R là Cacbon
b) CTHH của hợp chất R với oxi và hidro lần lượt là CO2, CH4
Ta có CTHH của h/c R với H là: RH4
<=> R mang hóa trị 4
<=> CTHH của h/c R với O là: RO2
Khối lượng mol của h/c RO2 là:
\(M_{RO_2}=\dfrac{m_O}{\%O}=\dfrac{16.2}{72,73\%}=44\left(\dfrac{g}{mol}\right)\)
\(\Leftrightarrow R+16.2=44\\ \Leftrightarrow R=12\left(\dfrac{g}{mol}\right)\\ \Rightarrow R.là.C\)
b, CTHH với oxi mik có ở trên rùi và CTHH với H có trong đề bài rùi
BT5: Thu gọn, chỉ ra phần hệ số và tìm bậc của các đơn thức sau: a, 5xy^2.(-3y)^2 b, x^2yz.(-2xy)^3 c, (-2x^2y)^2.8x^3yz^3 d, (-2xy^3)^2.(-2xyz)^3 e, (-5xy^3z).(-4x^2)^2 f, (2x^2y^3)^2.(-2xy)
a) 5xy² . (-3y)²
= 5xy² . 9y²
= (5.9).x.(y².y²)
= 45xy⁴
Hệ số: 45
Bậc: 5
b) x²yz . (-2xy)³
= x²yz . (-8x³y³)
= -8.(x².x³).(y.y³).z
= -8x⁵y⁴z
Hệ số: -8
Bậc: 10
c) (-2x²y)².8x³yz³
= 4x⁴y².8x³yz³
= (4.8).(x⁴.x³).(y².y).z³
= 32x⁷y³z³
Hệ số: 32
Bậc: 13
d) (-2xy³)².(-2xyz)³
= 4x²y⁶.(-8x³y³z³)
= [4.(-8)].(x².x³).(y⁶.y³).z³
= -32x⁵y⁹z³
Hệ số: -32
Bậc: 17
e) (-5xy³z).(-4x²)²
= (-5xy³z).(16x⁴)
= (-5.16).(x.x⁴).y³.z
= -80x⁵y³z
Hệ số: -80
Bậc: 9
f) (2x²y³)².(-2xy)
= (4x⁴y⁶).(-2xy)
= [4.(-2)].(x⁴.x).(y⁶.y)
= -8x⁵y⁷
Hệ số: -8
Bậc: 12
a: =5xy^2*9y^2=45xy^4
b: =x^2yz*(-8)x^3y^3=-8x^5y^4z
c: =4x^4y^2*8x^3yz^3=32x^7y^3z^3
d: =4x^2y^6*(-8)x^3y^3z^3=-32x^5y^9z^3
e: =-5xy^3z*16x^4=-80x^5y^3z
f: =4x^4y^6*(-2xy)=-8x^5y^7
BT4: Cho các chất sau: Cl2; HCl; MgCl2; CuCl2; ZnCl2;H2SO4 đặc, nguội; S. Chất nào tác dụng được với kim loại Al, Fe trong điều kiện thích hợp. Viết PTHH xảy ra BT5: Hoà tan hoàn toàn 8,1g bột kim loại Al vào dung dịch axit HCl 12%. a) Tính thể tích khí H2 sinh ra ở đktc b) Tính khối lượng dung dịch HCl phản ứng c) Tính khối lượng muối nhôm tạo thành.
Bài 4:
- Chất có pư với Al trong điều kiện thích hợp: Cl2, HCl, CuCl2, ZnCl2, S.
PT: \(2Al+3Cl_2\underrightarrow{t^o}2AlCl_3\)
\(2Al+6HCl\rightarrow2AlCl_3+3H_2\)
\(2Al+3CuCl_2\rightarrow2AlCl_3+3Cu\)
\(2Al+3ZnCl_2\rightarrow2AlCl_3+3Zn\)
\(2Al+3S\underrightarrow{t^o}Al_2S_3\)
- Chất có pư với Fe trong điều kiện thích hợp: Cl2, HCl, CuCl2, S.
PT: \(2Fe+3Cl_2\underrightarrow{t^o}2FeCl_3\)
\(Fe+2HCl\rightarrow FeCl_2+H_2\)
\(Fe+CuCl_2\rightarrow FeCl_2+Cu\)
\(Fe+S\underrightarrow{t^o}FeS\)
Bài 5:
Ta có: \(n_{Al}=\dfrac{8,1}{27}=0,3\left(mol\right)\)
PT: \(2Al+6HCl\rightarrow2AlCl_3+3H_2\)
a, \(n_{H_2}=\dfrac{3}{2}n_{Al}=0,45\left(mol\right)\Rightarrow V_{H_2}=0,45.24,79=11,1555\left(l\right)\)
b, \(n_{HCl}=3n_{Al}=0,9\left(mol\right)\)
\(\Rightarrow m_{ddHCl}=\dfrac{0,9.36,5}{12\%}=273,75\left(g\right)\)
c, \(n_{AlCl_3}=n_{Al}=0,3\left(mol\right)\)
\(\Rightarrow m_{AlCl_3}=0,3.133,5=40,05\left(g\right)\)