Giải phương trình \(\cos7x.\sin2x=-1\)

Những câu hỏi liên quan
Giải các phương trình
a) \(\dfrac{\cos2x}{\sin2x-1}=0\)
b) \(\cos\left(\sin x\right)=1\)
c) \(2\sin^2x-1+\cos3x=0\)
d) \(tan3x.tanx=1\)
e) \(\cos3x=-\cos7x\)
a: ĐKXĐ: sin 2x<>1
=>2x<>pi/2+k2pi
=>x<>pi/4+kpi
\(\dfrac{cos2x}{sin2x-1}=0\)
=>cos2x=0
=>2x=pi/2+kpi
=>x=pi/4+kpi/2
Kết hợp ĐKXĐ, ta được:
x=3/4pi+k2pi hoặc x=7/4pi+k2pi
b: cos(sinx)=1
=>sin x=kpi
=>sin x=0
=>x=kpi
c: \(2\cdot sin^2x-1+cos3x=0\)
=>cos3x+cos2x=0
=>cos3x=-cos2x=-sin(pi/2-2x)=sin(2x-pi/2)
=>cos3x=cos(pi/2-2x+pi/2)=cos(pi-2x)
=>3x=pi-2x+k2pi hoặc 3x=-pi+2x+k2pi
=>x=-pi+k2pi hoặc x=pi/5+k2pi/5
e: cos3x=-cos7x
=>cos3x=cos(pi-7x)
=>3x=pi-7x+k2pi hoặc 3x=-pi+7x+k2pi
=>x=pi/10+kpi/5 hoặc x=pi/4-kpi/2
Đúng 2
Bình luận (0)
Giải các phương trình sau:
a) √3.sin2x - cos2x + 1 = 0
b) 3sin4x + 4cos4x = 1
c) sin3x - √3.cos3x = 2cos5x
d) sinx(sinx + 2cosx) = 2
e) √3(sin2x + cos7x) = sin7x - cos2x
\(\text{c) }sin3x-\sqrt{3}cos3x=2cos5x\\ \Leftrightarrow\frac{1}{2}sin3x-\frac{\sqrt{3}}{2}cos3x=cos5x\\ \Leftrightarrow sin\frac{\pi}{6}\cdot sin3x-cos\frac{\pi}{6}\cdot cos3x=cos5x\\ \Leftrightarrow cos\left(3x+\frac{\pi}{6}\right)=-cos5x\\ \Leftrightarrow cos\left(3x+\frac{\pi}{6}\right)=cos\left(\pi-5x\right)\\ \Leftrightarrow\left[{}\begin{matrix}3x+\frac{\pi}{6}=\pi-5x+m2\pi\\3x+\frac{\pi}{6}=5x-\pi+n2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{5\pi}{48}+\frac{m\pi}{4}\\x=\frac{7\pi}{12}-n\pi\end{matrix}\right.\)
\(d\text{) }sinx\left(sinx+2cosx\right)=2\\ \Leftrightarrow cos^2x+\left(sinx-cosx\right)^2=0\\ \Leftrightarrow cosx=sinx=0\left(VN\right)\)
\(e\text{) }\sqrt{3}\left(sin2x+cos7x\right)=sin7x-cos2x\\ \Leftrightarrow\sqrt{3}sin2x+cos2x=sin7x-\sqrt{3}cos7x\\ \Leftrightarrow sin2x\cdot\frac{\sqrt{3}}{2}+cos2x\cdot\frac{1}{2}=sin7x\cdot\frac{1}{2}-cos7x\cdot\frac{\sqrt{3}}{2}\\ \Leftrightarrow sin2x\cdot cos\frac{\pi}{3}+cos2x\cdot sin\frac{\pi}{3}=sin7x\cdot cos\frac{\pi}{3}-cos7x\cdot sin\frac{\pi}{3}\\ \Leftrightarrow sin\left(2x-\frac{\pi}{3}\right)=sin\left(7x-\frac{\pi}{3}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{3}=7x-\frac{\pi}{3}+m2\pi\\2x-\frac{\pi}{3}=\frac{4\pi}{3}-7x+n2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{-m2\pi}{5}\\x=\frac{5\pi}{27}+\frac{n2\pi}{9}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
\(\text{a) }\sqrt{3}sin2x-cos2x+1=0\\ \Leftrightarrow\frac{\sqrt{3}}{2}sin2x-\frac{1}{2}cos2x=-\frac{1}{2}\\ \Leftrightarrow cos\frac{\pi}{3}\cdot cos2x-sin\frac{\pi}{3}\cdot sin2x=\frac{1}{2}\\ \Leftrightarrow cos\left(2x-\frac{\pi}{3}\right)=cos\frac{\pi}{3}\\ \Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{3}=\frac{\pi}{3}+m2\pi\\2x-\frac{\pi}{3}=-\frac{\pi}{3}+n2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{3}+m\pi\\x=n\pi\end{matrix}\right.\)
\(\text{b) }pt\Leftrightarrow sin4x=\frac{1-4cosx}{3}\\ \Leftrightarrow sin^24x+cos^24x=\left(\frac{1-cos4x}{3}\right)^2+cos^24x=1\\ \Leftrightarrow\left[{}\begin{matrix}cos4x=1\\cos4x=-\frac{4}{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}cos4x=1\\cos4x=-\frac{4}{5}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\frac{k\pi}{2}\\x=\frac{arccos\left(-\frac{4}{5}\right)}{4}+\frac{k\pi}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Giải phương trình
3
sin
7
x
-
cos
7
x
2
sin
5
x
-
π
6
Đọc tiếp
Giải phương trình 3 sin 7 x - cos 7 x = 2 sin 5 x - π 6

![]()
![]()

Giải các phương trình:
\(a,sin2x.sin3x=cos2x.cos3x\)
\(b,cos2x.cos5x=cos7x\)
a) cos5x.cosx= cos4x.cos2x+3cos^2x+1
b)cos7x - sin2x-1=0
Giải phương trình :
sin2x -\(\dfrac{\sqrt{3}}{2}\)sin2x+ 2cos2x =1
Thấy cosx= 0 là nghiệm của phương trình => \(x=\dfrac{\pi}{2}+k\pi\)
Xét cosx khác 0, chia cả 2 vế cho cos^2 x
\(\Leftrightarrow\tan^2x-\sqrt{3}\tan x+2=1+\tan^2x\)
\(\Leftrightarrow\tan x=\dfrac{\sqrt{3}}{3}\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\)
Đúng 0
Bình luận (0)
Giải phương trình
sin
2
x
1
. A.
x
π
2
+
k
2
π
,
k
∈
ℤ
B.
x
π
4
+
k
2
π
,
k
∈
ℤ
C.
x
π...
Đọc tiếp
Giải phương trình sin 2 x = 1 .
A. x = π 2 + k 2 π , k ∈ ℤ
B. x = π 4 + k 2 π , k ∈ ℤ
C. x = π 4 + k π , k ∈ ℤ
D. x = π + k 4 π , k ∈ ℤ
Giải phương trình:
\(\cos3x+\cos7x=2\sin^2\left(\dfrac{\pi}{4}-\dfrac{5x}{2}\right)+2\cos^2\dfrac{9\pi}{2}\)
Đề sai nhiều chỗ vậy, lần sau ghi đúng đề đi.
\(cos3x+sin7x=2sin^2\left(\dfrac{\pi}{4}-\dfrac{5x}{2}\right)+2cos^2\dfrac{9x}{2}\)
\(\Leftrightarrow cos3x+sin7x=cos\left(\dfrac{\pi}{2}-5x\right)+1-2cos^2\dfrac{9x}{2}\)
\(\Leftrightarrow cos3x+sin7x=sin5x-cos9x\)
\(\Leftrightarrow2cos6x.cos3x+2cos6x.sinx=0\)
\(\Leftrightarrow2cos6x.\left(cos3x+sinx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos6x=0\\cos3x+sinx=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}cos6x=0\\cos3x+cos\left(\dfrac{\pi}{2}-x\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}cos6x=0\\2cos\left(\dfrac{\pi}{4}+x\right).cos\left(2x-\dfrac{\pi}{4}\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}cos6x=0\\cos\left(\dfrac{\pi}{4}+x\right)=0\\cos\left(2x-\dfrac{\pi}{4}\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}6x=\dfrac{\pi}{2}+k\pi\\\dfrac{\pi}{4}+x=\dfrac{\pi}{2}+k\pi\\2x-\dfrac{\pi}{4}=\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{12}+\dfrac{k\pi}{6}\\x=\dfrac{\pi}{4}+k\pi\\x=\dfrac{3\pi}{8}+\dfrac{k\pi}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Giải phương trình
sin
2
x
+
2
sin
x
-
π
4
1
Đọc tiếp
Giải phương trình sin 2 x + 2 sin x - π 4 = 1
![]()
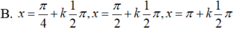
![]()
![]()