Cho hàm số \(_{\left|x+1\right|\left(x-2\right)}\). Tìm khoảng đồng biến, nghịch biến của hs.

Những câu hỏi liên quan
tìm khoảng đồng biến và nghịch biến của hàm số sau
a) y' = \(\left(2x-3\right)\left(x^2-1\right)\)
b) y' = \(-\left(x+2\right)\left(2x+5\right)\)
a: Đặt y'>0
=>(2x-3)(x^2-1)>0
Th1: 2x-3>0 và x^2-1>0
=>x>3/2 và (x>1 hoặc x<-1)
=>x>3/2
TH2: 2x-3<0 và x^2-1<0
=>x<3/2 và -1<x<1
=>-1<x<1
=>Hàm số đồng biến khi x>3/2 hoặc -1<x<1
Đặt y'<0
=>(2x-3)(x^2-1)<0
TH1: 2x-3>0 và x^2-1<0
=>x>3/2 và -1<x<1
=>Loại
TH2: 2x-3<0 và x^2-1>0
=>x<3/2 và (x>1 hoặc x<-1)
=>1<x<3/2 hoặc x<-1
=>Hàm số nghịch biến khi 1<x<3/2 hoặc x<-1
b: Đặt y'>0
=>(x+2)(2x+5)<0
=>-5/2<x<-2
=>hàm số đồng biến khi -5/2<x<-2
Đặt y'<0
=>(x+2)(2x+5)>0
=>x>-2 hoặc x<-5/2
=>Hàm số nghịch biến khi x>-2 hoặc x<-5/2
Đúng 0
Bình luận (0)
tìm khoảng đồng biến và nghịch biến của hàm số sau
a) \(y'=\left(x-3\right)^3\left(x-1\right)^{22}\left(-3x-6\right)^7\)
b) \(y'=\left(4x-3\right)^3\left(x^2-1\right)^{21}\left(3x-9\right)^7\)
a: \(y'< 0\)
=>\(\left(x-3\right)^3\cdot\left(x-1\right)^{22}\cdot\left(-3x-6\right)^7< 0\)
=>\(\left(x-3\right)\left(-3x-6\right)< 0\)
=>\(\left(x+2\right)\left(x-3\right)>0\)
=>\(\left[{}\begin{matrix}x>3\\x< -2\end{matrix}\right.\)
y'>0
=>\(\left(x+2\right)\left(x-3\right)< 0\)
=>\(-2< x< 3\)
y'=0
=>\(\left[{}\begin{matrix}x-3=0\\x-1=0\\-3x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\\x=-2\end{matrix}\right.\)
Ta có bảng xét dấu sau:
| x | \(-\infty\) -2 1 3 +\(\infty\) |
| y' | - 0 + 0 + 0 - |
Vậy: Hàm số đồng biến trên các khoảng \(\left(-2;1\right);\left(1;3\right)\)
Hàm số nghịch biến trên các khoảng \(\left(-\infty;-2\right);\left(3;+\infty\right)\)
b: y'<0
=>\(\left(4x-3\right)^3\cdot\left(x^2-1\right)^{21}\left(3x-9\right)^7< 0\)
=>\(\left(4x-3\right)\left(3x-9\right)\left(x^2-1\right)< 0\)
=>\(\left(4x-3\right)\left(x-3\right)\left(x^2-1\right)< 0\)
TH1: \(\left\{{}\begin{matrix}\left(4x-3\right)\left(x-3\right)>0\\x^2-1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left[{}\begin{matrix}x>3\\x< \dfrac{3}{4}\end{matrix}\right.\\-1< x< 1\end{matrix}\right.\Leftrightarrow-1< x< \dfrac{3}{4}\)
TH2: \(\left\{{}\begin{matrix}\left(4x-3\right)\left(x-3\right)< 0\\x^2-1>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{4}< x< 3\\\left[{}\begin{matrix}x>1\\x< -1\end{matrix}\right.\end{matrix}\right.\Leftrightarrow1< x< 3\)
y'>0
=>\(\left(4x-3\right)\left(x-3\right)\left(x^2-1\right)>0\)
TH1: \(\left\{{}\begin{matrix}\left(4x-3\right)\left(x-3\right)>0\\x^2-1>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left[{}\begin{matrix}x>3\\x< \dfrac{3}{4}\end{matrix}\right.\\\left[{}\begin{matrix}x>1\\x< -1\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x>3\\x< -1\end{matrix}\right.\)
TH2: \(\left\{{}\begin{matrix}\left(4x-3\right)\left(x-3\right)< 0\\x^2-1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{3}{4}< x< 3\\-1< x< 1\end{matrix}\right.\Leftrightarrow\dfrac{3}{4}< x< 1\)
Ta sẽ có bảng xét dấu sau đây:
| x | \(-\infty\) -1 3/4 1 3 +\(\infty\) |
| y' | + 0 - 0 + 0 - 0 + |
Vậy: Hàm số đồng biến trên các khoảng \(\left(-\infty;-1\right);\left(\dfrac{3}{4};1\right);\left(3;+\infty\right)\)
Hàm số nghịch biến trên các khoảng \(\left(-1;\dfrac{3}{4}\right);\left(1;3\right)\)
Đúng 1
Bình luận (0)
Hàm số \(y = \cos x\) đồng biến hay nghịch biến trên khoảng \(\left( { - 2\pi ; - \pi } \right)\)
Hàm số \(y = \cos x\)đồng biến trên mỗi khoảng \(\left( { - \pi + k2\pi ;k2\pi } \right)\), nghịch biến trên mỗi khoảng \(\left( {k2\pi ;\pi + k2\pi } \right)\) với \(k \in Z\)
Do \(\left( { - 2\pi ; - \pi } \right) = \left( { - 2\pi ;\pi - 2\pi } \right)\) nên hàm số \(y = \cos x\) nghịch biến trên khoảng \(\left( { - 2\pi ; - \pi } \right)\)
Đúng 0
Bình luận (0)
Cho hàm số \(y = f\left( x \right)\) có đồ thị như Hình 9. Chỉ ra khoảng đồng biến và khoảng nghịch biến của hàm số \(y = f\left( x \right)\).
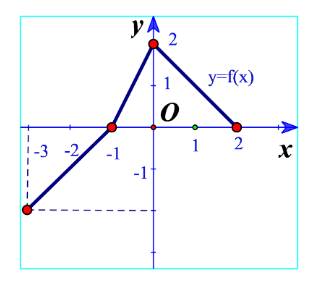
Từ đồ thị hàm số ta thấy khi x tăng từ -3 đến -1 và từ -1 đến 0 thì đồ thị đi lên nên hàm số đồng biến trên các khoảng (-3;-1) và (-1;0).
Khi x tăng từ 0 đến 2 thì đồ thị đi xuống nên hàm số nghịch biến trên (0;2).
Đúng 0
Bình luận (0)
xét tính đồng biến nghịch biến của các hàm số trên
\(y=f\left(x\right)=x^2-2x+3\) trên khoảng \(_{\left(1;+\infty\right)}\)
y=f(x)=\(\sqrt{3-x}\) trên khoảng \(\left(-\infty;3\right)\)
tìm các giá trị của m để hàm số
a) \(y=\dfrac{mx+25}{x+m}\) nghịch biến trên khoảng \(\left(-\infty;1\right)\)
b) \(y=\dfrac{x+2}{x+m}\) nghịch biến trên khoảng \(\left(-\infty;-5\right)\)
Bài 10. Xét tính đồng biến và nghịch biến của các hàm số sau trên các khoảng đã chỉ raa: fleft(xright)2x^2-4x+3 trên các khoảng left(3;+inftyright) và (-10;1)b: fleft(xright)-3x^2+6x+1 trên các khoảng left(1;+inftyright) và (-10;-2)c: fleft(xright)dfrac{x}{x-2} trên khoảng left(-infty;2right)d: fleft(xright)-dfrac{1}{x+1} trên các khoảng (-3;-2) và left(-1;+inftyright)e: fleft(xright)x^{2020}+x^2-3 trên khoảng left(0;+inftyright)
Đọc tiếp
Bài 10. Xét tính đồng biến và nghịch biến của các hàm số sau trên các khoảng đã chỉ ra
a: \(f\left(x\right)=2x^2-4x+3\) trên các khoảng \(\left(3;+\infty\right)\) và (-10;1)
b: \(f\left(x\right)=-3x^2+6x+1\) trên các khoảng \(\left(1;+\infty\right)\) và (-10;-2)
c: \(f\left(x\right)=\dfrac{x}{x-2}\) trên khoảng \(\left(-\infty;2\right)\)
d: \(f\left(x\right)=-\dfrac{1}{x+1}\) trên các khoảng (-3;-2) và \(\left(-1;+\infty\right)\)
e: \(f\left(x\right)=x^{2020}+x^2-3\) trên khoảng \(\left(0;+\infty\right)\)
a) Đk:\(x\in R\)
TH1:Xét \(x\in\left(3;+\infty\right)\)
Lấy \(x_1;x_2\in\left(3;+\infty\right)\) thỏa mãn \(x_1\ne x_2\)
Xét \(I=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{2x_1^2-4x_1+3-\left(2x_2^2-4x_2+3\right)}{x_1-x_2}\)\(=2\left(x_1+x_2\right)-4\)
Do \(x_1;x_2\in\left(3;+\infty\right)\)\(\Rightarrow2\left(x_1+x_2\right)>12\Leftrightarrow2\left(x_1+x_2\right)-4>8>0\)
\(\Rightarrow I>0\)
Hàm đồng biến trên \(\left(3;+\infty\right)\)
TH2:Xét \(x\in\left(-10;1\right)\)
Lấy \(x_1;x_2\in\left(-10;1\right):x_1\ne x_2\)
Xét \(I=2\left(x_1+x_2\right)-4\)
Do \(x_1< 1;x_2< 1\Rightarrow2\left(x_1+x_2\right)< 4\Rightarrow I=2\left(x_1+x_2\right)-4< 0\)
Hàm nb trên khoảng \(\left(-10;1\right)\)
b)Làm tương tự,hàm nb trên \(\left(1;+\infty\right)\) và đb trên \(\left(-10;-2\right)\)
c)Đk: \(x\in R\backslash\left\{2\right\}\)
=>Hàm số xác định trên \(\left(-\infty;2\right)\)
Lấy \(x_1;x_2\in\left(-\infty;2\right):x_1\ne x_2\)
Xét \(I=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{\dfrac{x_1}{x_1-2}-\dfrac{x_2}{x_2-2}}{x_1-x_2}=\dfrac{-2}{\left(x_1-2\right)\left(x_2-2\right)}\)
Do \(x_1;x_2< 2\Rightarrow\left(x_1-2\right)\left(x_2-2\right)>0\)
\(\Rightarrow I=-\dfrac{2}{\left(x_1-2\right)\left(x_2-2\right)}< 0\)
Hàm nb trên \(\left(-\infty;2\right)\)
d)\(I=\dfrac{1}{\left(x_1+1\right)\left(x_2+1\right)}\)
Hàm đb trên \(\left(-1;+\infty\right)\) ; \(\left(-3;-2\right)\)
e)TXĐ:D=R
Lấy \(x_1;x_2\in\left(0;+\infty\right):x_1< x_2\)
\(T=f\left(x_1\right)-f\left(x_2\right)=x_1^{2020}+x_1^2-3-x_2^{2020}-x_2^2+3=x_1^{2020}-x_2^{2020}+x_1^2-x_2^2\)
Do \(x_1< x_2\Rightarrow x_1^{2020}< x_2^{2020};x_1^2< x_2^2\)
\(\Rightarrow T=x_1^{2020}-x_2^{2020}+x_1^2-x_2^2< 0\)
Hàm đb trên \(\left(0;+\infty\right)\)
Đúng 5
Bình luận (0)
Vẽ đồ thị của các hàm số \(y=3x+1\) và \(y=-2x^2\). Hãy cho biết:
a) Hàm số \(y=3x+1\) đồng biến hay nghịch biến trên R.
b) Hàm số \(y=-2x^2\) đồng biến hay nghịch biến trên mỗi khoảng: \(\left(-\infty;0\right)\) và \(\left(0;+\infty\right)\)
Vẽ đồ thị \(y = 3x + 1;y = - 2{x^2}\)

a) Trên \(\mathbb{R}\), đồ thị \(y = 3x + 1\) đi lên từ trái sang phải, như vậy hàm số \(y = 3x + 1\) đồng biến trên \(\mathbb{R}\)
b) Trên khoảng \(\left( { - \infty ;0} \right)\), đồ thị \(y = - 2{x^2}\)đi lên từ trái sang phải với mọi \(x \in \left( { - \infty ;0} \right)\) , như vậy hàm số đồng biến trên \(\left( { - \infty ;0} \right)\)
Trên khoảng \(\left( {0; + \infty } \right)\), đồ thị \(y = - 2{x^2}\)đi xuống từ trái sang phải với mọi \(x \in \left( {0; + \infty } \right)\) , như vậy hàm số nghịch biến trên \(\left( {0; + \infty } \right)\)
Đúng 0
Bình luận (0)
Cho hàm số \(y = \frac{1}{x}\). Chứng tỏ hàm số đã cho:
a) Nghịch biến trên khoảng \(\left( {0; + \infty } \right)\);
b) Nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
a) Tập xác định \(D = \mathbb{R}\backslash \left\{ 0 \right\}\).
Lấy \({x_1},{x_2} \in \left( {0; + \infty } \right)\) sao cho \({x_1} < {x_2}\).
Xét \(f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = \frac{1}{{{x_1}}} - \frac{1}{{{x_2}}} = \frac{{{x_2} - {x_1}}}{{{x_1}{x_2}}}\)
Do \({x_1} < {x_2}\) nên \({x_2} - {x_1} > 0\)
\({x_1},{x_2} \in \left( {0; + \infty } \right) \Rightarrow {x_1}{x_2} > 0\)
\( \Rightarrow f\left( {{x_1}} \right) - f\left( {{x_2}} \right) > 0 \Leftrightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
Vậy hàm số nghịch biến trên \(\left( {0; + \infty } \right)\).
b) Lấy \({x_1},{x_2} \in \left( { - \infty ;0} \right)\) sao cho \({x_1} < {x_2}\).
Xét \(f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = \frac{1}{{{x_1}}} - \frac{1}{{{x_2}}} = \frac{{{x_2} - {x_1}}}{{{x_1}{x_2}}}\)
Do \({x_1} < {x_2}\) nên \({x_2} - {x_1} > 0\)
\({x_1},{x_2} \in \left( { - \infty ;0} \right) \Rightarrow {x_1}{x_2} > 0\)(Cùng dấu âm nên tích cũng âm)
\( \Rightarrow f\left( {{x_1}} \right) - f\left( {{x_2}} \right) > 0 \Leftrightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
Vậy hàm số nghịch biến trên \(\left( { - \infty ;0} \right)\).
Đúng 0
Bình luận (0)











