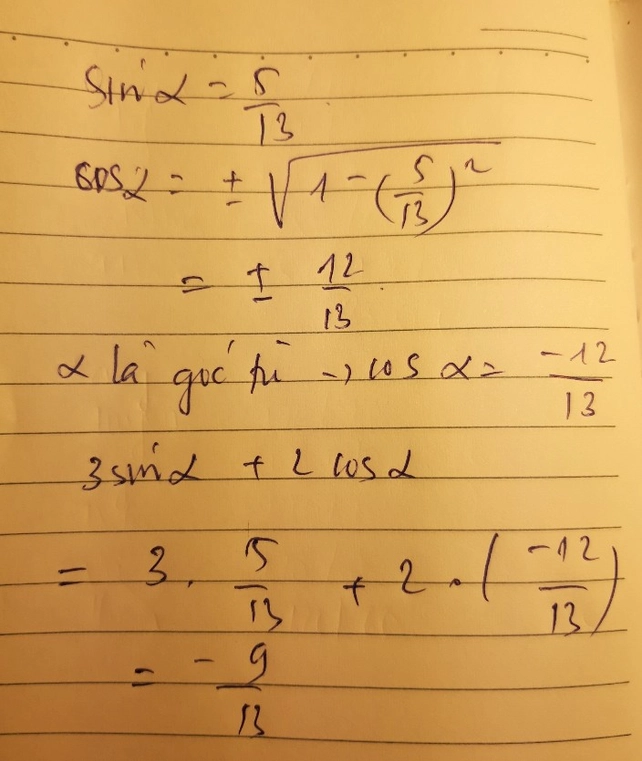cho tan\(x\)=-3. tính giá trị của biểu thức A= \(\frac{sin^2x+sinx.cosx+5}{3sin^2x-2cos^2x}\)

Những câu hỏi liên quan
Cho biểu thức: B=\(\left[\dfrac{x+1}{2x-2}+\dfrac{3}{x^2-1}-\dfrac{x+3}{2x+2}\right].\dfrac{4x^2-4}{5}\)
a, Tìm điều kiện của x để giá trị của biểu thức được xác định
b, Chứng minh rằng: Khi giá trị của biểu thức được xác định thì nó không phụ thuộc vào giá trị
a, ĐKXĐ: \(x\ne1;x\ne-1\)
b, Với \(x\ne1;x\ne-1\)
\(B=\left[\dfrac{x+1}{2\left(x-1\right)}+\dfrac{3}{\left(x-1\right)\left(x+1\right)}-\dfrac{x+3}{2\left(x+1\right)}\right]\cdot\dfrac{4\left(x^2-1\right)}{5}\\ =\left[\dfrac{x^2+2x+1+6-x^2-2x+3}{2\left(x-1\right)\left(x+1\right)}\right]\cdot\dfrac{4\left(x^2-1\right)}{5}\\ =\dfrac{5}{x^2-1}\cdot\dfrac{4\left(x^2-1\right)}{5}\\ =4\)
=> ĐPCM
Đúng 0
Bình luận (0)
Cho biểu thức: A = (x + 1)(x – 2) – x(2x – 3) + 4 + 2x2
a) Chứng minh: A = x2 + 2x + 2
b) Tính giá trị của biểu thức A khi x =
c) Chứng minh biểu thức A luôn dương với mọi x.
a: \(A=\left(x+1\right)\left(x-2\right)-x\left(2x-3\right)+2x^2+4\)
\(=x^2-x-2-2x^2+3x+2x^2+4\)
\(=x^2+2x+2\)
Đúng 3
Bình luận (0)
\(a,A=x^2-x-2-2x^2+3x+4+2x^2=x^2+2x+2\\ c,A=\left(x^2+2x+1\right)+1=\left(x+1\right)^2+1\ge1>0\)
Đúng 2
Bình luận (0)
Cho biểu thức P=\(\frac{x+2}{x+3}-\frac{5}{x^2+x-6}+\frac{1}{2x}\)
a Tính giá trị biểu thức P khi x^2 -9 =0
điều kiện xác định của phân thức là x khác 0 và x khác -3
nên bạn nhập phân thức vào máy rồi thay x =3 ta có P =1/6
Đúng 0
Bình luận (3)
điều kiện xác định là x = 3 và x = -3 thay các giá trị của x mà mk ns vào biểu thức là ra thôi k khó![]()
Đúng 0
Bình luận (0)
Cho tan a = 1/3 . Tính giá trị của biểu thức
M= cos a - sin a / cos a + sin a
1) Tìm x, bIết:| 2x+5 |+4\(\ge\)25
2) Tìm giá trị nhỏ nhất của biểu thức:
a) A= |2x-3| - 5
b) B= |2x-1|+|3-2x|+5
3) Tìm giá trị lớn nhất của biểu thức:
A= -|2X+1|+7
B= |2x+3|-|2x+2|
1) \(\left|2x+5\right|\ge21\Rightarrow2x+5\ge21\)hoặc \(2x+5
Đúng 0
Bình luận (0)
2b) Áp dụng bất đẳng thức giá trị tuyệt đối: |a| + |b| \(\ge\) |a + b|. Dấu "=" xảy ra khi tích a.b \(\ge\) 0
Ta có: B = |2x - 1| + |3 - 2x| + 5 \(\ge\) |2x - 1+3 - 2x| + 5 = |2| + 5 = 7
=> Min B = 7 khi
(2x - 1)( 3 - 2x) \(\ge\) 0 => (2x - 1)(2x - 3) \(\le\) 0
Mà 2x - 1 > 2x - 3 nên 2x - 1 \(\ge\) 0 và 2x - 3 \(\le\) 0
=> x \(\ge\) 1/2 và x \(\le\) 3/2
Đúng 0
Bình luận (0)
Cho biểu thức P= \(\frac{x+2}{x+3}+\frac{5}{x^2+x-6}+\frac{1}{2x}\)
a, Rút gọn p
b,Tính giá trị của P khi x^2-9 = 0
c, Tìm các gì trị nguyên của x để P cũng có là Gía trị nguyên
a. Tính giá trị của phân thức N =\(\dfrac{x^3-1}{x^2-2x+1}\) tại x = -1
b. Tính giá trị của phân thức M =\(\dfrac{x^3+8}{x^2-2x+4}\) tại x = -2
a: Ta có: \(N=\dfrac{x^3-1}{x^2-2x+1}\)
\(=\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{\left(x-1\right)^2}\)
\(=\dfrac{x^2+x+1}{x-1}\)
\(=\dfrac{\left(-1\right)^2+\left(-1\right)+1}{-1-1}=\dfrac{1}{-2}=-\dfrac{1}{2}\)
b: Ta có: \(M=\dfrac{x^3+8}{x^2-2x+4}\)
\(=\dfrac{\left(x+2\right)\left(x^2-2x+4\right)}{x^2-2x+4}\)
\(=x+2=0\)
Đúng 2
Bình luận (0)
a) \(N=\dfrac{x^3-1}{x^2-2x+1}=\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{\left(x-1\right)^2}=\dfrac{x^2+x+1}{x-1}=\dfrac{\left(-1\right)^2-1+1}{-1-1}=-\dfrac{1}{2}\)b) \(M=\dfrac{x^3+8}{x^2-2x+4}=\dfrac{\left(x+2\right)\left(x^2-2x+4\right)}{x^2-2x+4}=x+2=-2+2=0\)
Đúng 1
Bình luận (0)
1. Tìm các giá trị nguyên của x để biểu thức sau có giá trị lớn nhất:
a.A=\(\frac{2}{5-x}\) b. B=\(\frac{19-2x}{9-x}\)
2. Cho hai biểu thức: A=\(\frac{4x-7}{x-2}\); B=\(\frac{3x-9x+2}{x-3}\). Tìm các giá trị nguyên của x để cả hai biểu thức cùng có giá trị nguyên.
Giúp mik cho góc apha là góc tù và sin apha =5/13 giá trị của biểu thức 3sin apha +2cos apha là
A 3 b -9/13 C-3 d 9/13
Xem chi tiết