Cho đg tròn (C) có pt \(x^2+y^2-2x.cos\alpha-2y.sin\alpha-8=0\) với α cho trước. Tính bkinh của (C)

Những câu hỏi liên quan
Câu 50**: Cho góc nhọn α tuỳ ý giá trị biểu thức dfrac{tanalpha}{cotalpha}+dfrac{cotalpha}{tanalpha}-dfrac{sin^2alpha}{cos^2alpha}bằng A. tan^2alpha ; B . cot^2 α ; C . 0 ; D. 1 .giải hộ mik vs
Đọc tiếp
Câu 50**: Cho góc nhọn α tuỳ ý giá trị biểu thức \(\dfrac{tan\alpha}{cot\alpha}+\dfrac{cot\alpha}{tan\alpha}-\dfrac{sin^2\alpha}{cos^2\alpha}\)bằng
A. \(tan^2\alpha\) ; B . \(cot^2\) α ; C . 0 ; D. 1 .
giải hộ mik vs
Trong mặt phẳng tọa độ Oxy , với α , a , b là những số cho trước , xét phép biến hình F biến mỗi điểm M(x ; y) thành điểm M(x ; y) , trong đó : begin{cases}xxcosalpha-ysinalpha+ayxsinalpha+ycosalpha+bend{cases} a) cho 2 điểm M(x1 ; y1) , N(x2 ; y2) và gọi M , N lần lượt là ảnh của M , N qua phép F . Hãy tìm tọa độ của M và N .b) tính khoảng cách d giữa M và N ; khoảng cách d giữa M và N .c) phép F có phải ;à phép dời hình hay không ?d) khi α0 , chứng tỏ rằng F là phép tịnh tiến .
Đọc tiếp
Trong mặt phẳng tọa độ Oxy , với α , a , b là những số cho trước , xét phép biến hình F biến mỗi điểm M(x ; y) thành điểm M'(x' ; y') , trong đó :
\(\begin{cases}x'=x\cos\alpha-y\sin\alpha+a\\y'=x\sin\alpha+y\cos\alpha+b\end{cases}\)
a) cho 2 điểm M(x1 ; y1) , N(x2 ; y2) và gọi M' , N' lần lượt là ảnh của M , N qua phép F . Hãy tìm tọa độ của M' và N' .
b) tính khoảng cách d giữa M và N ; khoảng cách d' giữa M' và N' .
c) phép F có phải ;à phép dời hình hay không ?
d) khi α=0 , chứng tỏ rằng F là phép tịnh tiến .
a) Gọi M' (x₁' ; y₁' ), N' (x₂' ; y₂ )
* M' là ảnh của M qua phép F, nên toạ độ M' thoả:
{x₁' = x₁.cosα – y₁.sinα + a
{y₁' = x₁.sinα + y₁.cosα + b
* N' là ảnh của N qua phép F, nên toạ độ N' thoả:
{x₂' = x₂.cosα – y₂.sinα + a
{y₂' = x₂.sinα + y₂.cosα + b
b) * Khoảng cách d giữa M và N là:
d = MN = √ [(x₂ - x₁)² + (y₂ - y₁)²]
* Khoảng cách d' giữa M' và N' là:
d' = M'N' = √ [(x₂' - x₁' )² + (y₂' - y₁' )²]
= √ {[x₂.cosα – y₂.sinα + a - (x₁.cosα – y₁.sinα + a)]² + [x₂.sinα + y₂.cosα + b - (x₁.sinα + y₁.cosα + b)]²}
= √ {[cosα(x₂ - x₁) - sinα(y₂ - y₁)]² + [sinα(x₂ - x₁) + cosα(y₂ - y₁)]²}
= √ [(x₂ - x₁)².(cos²α + sin²α) + (y₂ - y₁)².(cos²α + sin²α)]
= √ [(x₂ - x₁)² + (y₂ - y₁)²]
c) Phép F là phép dời hình vì: MN = M'N' = √ [(x₂ - x₁)² + (y₂ - y₁)²]
d) Khi α = 0 ⇒ cosα = 1, sinα = 0
Suy ra:
{x' = x + a
{y' = y + b
Đây là biểu thức toạ độ của phép tịnh tiến. Vậy F là phép tịnh tiến
Đúng 0
Bình luận (0)
Tính các giá trị lượng giác của góc α, nếu:
a) \(\sin \alpha = \frac{5}{{13}}\) và \(\frac{\pi }{2} < \alpha < \pi \)
b) \(\cos \alpha = \frac{2}{5}\) và \(0 < \alpha < 90^\circ \)
c) \(\tan \alpha = \sqrt 3 \) và \(\pi < \alpha < \frac{{3\pi }}{2}\)
d) \(\cot \alpha = \frac{1}{2}\) và \(270^\circ < \alpha < 360^\circ \)
Trong các hệ thức sau , hệ thức nào sai ?Nếu sai hãy sửa lại cho đúng và chứng minh các hệ thức đúng còn lại ?
A.frac{sin^2alpha+1}{2left(1-sin^2alpharight)}+frac{1+cos^2alpha}{2left(1-cos^2alpharight)}+1left(tanalpha+cotalpharight)^2
B.frac{1-4sin^2x.cos^2x}{4sin^2x.cos^2x}frac{1+tan^4x-2tan^2x}{4tan^2x}
C.frac{sinx+tanx}{tanx}1+sinx+cotx
D.tanx+frac{cosx}{1+sinx}frac{1}{cosx}
Đọc tiếp
Trong các hệ thức sau , hệ thức nào sai ?Nếu sai hãy sửa lại cho đúng và chứng minh các hệ thức đúng còn lại ?
\(A.\frac{sin^2\alpha+1}{2\left(1-sin^2\alpha\right)}+\frac{1+cos^2\alpha}{2\left(1-cos^2\alpha\right)}+1=\left(tan\alpha+cot\alpha\right)^2\)
\(B.\frac{1-4sin^2x.cos^2x}{4sin^2x.cos^2x}=\frac{1+tan^4x-2tan^2x}{4tan^2x}\)
\(C.\frac{sinx+tanx}{tanx}=1+sinx+cotx\)
\(D.tanx+\frac{cosx}{1+sinx}=\frac{1}{cosx}\)
\(\frac{sin^2a+1}{2.cos^2a}+\frac{1+cos^2a}{2.sin^2a}+1=\frac{tan^2a}{2}+\frac{1}{2cos^2a}+\frac{cot^2a}{2}+\frac{1}{2sin^2a}+1\)
\(=\frac{1}{2}\left(tan^2a+1+tan^2a+cot^2a+1+cot^2a+2\right)\)
\(=\frac{1}{2}\left(2tan^2a+4+2cot^2a\right)=tan^2a+2+cot^2a=\left(tana+cota\right)^2\)
B.
\(\frac{1-4sin^2a.cos^2a}{4sin^2a.cos^2a}=\frac{\frac{1}{cos^4a}-\frac{4sin^2a}{cos^2a}}{\frac{4sin^2a}{cos^2a}}=\frac{\left(\frac{1}{cos^2a}\right)^2-4tan^2a}{4tan^2a}=\frac{\left(1+tan^2a\right)^2-4tan^2a}{4tan^2a}\)
\(=\frac{tan^4a-2tan^2a+1}{4tan^2a}\)
C.
\(\frac{sina+tana}{tana}=\frac{sina}{tana}+1=1+sina.\frac{cosa}{sina}=1+cosa\)
D.
\(tana+\frac{cosa}{1+sina}=\frac{sina}{cosa}+\frac{cosa\left(1-sina\right)}{1-sin^2a}=\frac{sina.cosa}{cos^2a}+\frac{cosa-cosa.sina}{cos^2a}\)
\(=\frac{sina.cosa+cosa-sina.cosa}{cos^2a}=\frac{cosa}{cos^2a}=\frac{1}{cosa}\)
Câu C sai
Đúng 0
Bình luận (0)
Cho cot α = 3. Tính giá trị của các biểu thức sau
a) \(A=\dfrac{3sin\alpha-cos\alpha}{2sin\alpha+cos\alpha}\)
b)\(B=\dfrac{sin^2\alpha-3sin\alpha.cos\alpha+2}{2sin^2\alpha+sin\alpha.cos\alpha+cos^2\alpha}\)
Giúp em với ạ, em đang cần gấp!
\(A=\dfrac{\dfrac{3sina}{sina}-\dfrac{cosa}{sina}}{\dfrac{2sina}{sina}+\dfrac{cosa}{sina}}=\dfrac{3-cota}{2+cota}=\dfrac{3-3}{2+3}=0\)
\(B=\dfrac{\dfrac{sin^2a}{sin^2a}-\dfrac{3sina.cosa}{sin^2a}+\dfrac{2}{sin^2a}}{\dfrac{2sin^2a}{sin^2a}+\dfrac{sina.cosa}{sin^2a}+\dfrac{cos^2a}{sin^2a}}=\dfrac{1-3cota+2\left(1+cot^2a\right)}{2+cota+cot^2a}=\dfrac{1-3.3+2\left(1+3^2\right)}{2+3+3^2}=...\)
Đúng 7
Bình luận (2)
a. \(A=\dfrac{3sin\alpha-cos\alpha}{2sin\alpha+cos\alpha}=\dfrac{3\dfrac{sin\alpha}{cos\alpha}-1}{2\dfrac{sin\alpha}{cos\alpha}+1}=\dfrac{3.\dfrac{1}{3}-1}{2.\dfrac{1}{3}+1}=0\)
b.\(B=\dfrac{sin^2\alpha-3sin\alpha.cos\alpha+2}{2sin^2\alpha+sin\alpha.cos\alpha+cos^2\alpha}\)\(=\dfrac{1-\dfrac{3cos\alpha}{sin\alpha}+\dfrac{2}{sin^2\alpha}}{2+\dfrac{cos\alpha}{sin\alpha}+\dfrac{cos^2\alpha}{sin^2\alpha}}=\dfrac{1-3.3+\dfrac{2}{sin^2\alpha}}{2+3+3^2}\)
Mà \(\dfrac{cos\alpha}{sin\alpha}=3,cos^2\alpha+sin^2\alpha=1\Rightarrow sin^2\alpha=\dfrac{1}{10}\)
\(B=\dfrac{1-3.3+\dfrac{2}{\dfrac{1}{10}}}{2+3+3^2}=\dfrac{6}{7}\)
Đúng 2
Bình luận (0)
Giải pt sau với \(\alpha\)là tham số ; x là ẩn
\(\alpha\frac{9x^8+84x^6+126x^4+36x^2+1}{x^8+36x^6+126x^4+84x^2+9}+x\frac{9\alpha^8+84\alpha^6+126\alpha^4+36\alpha^2+1}{\alpha^8+36\alpha^6+126\alpha^4+84\alpha^2+9}=0\)
\(\Leftrightarrow\frac{\left(x+a\right)\left(3a^2x^2+a^2+8ax+x^2+3\right)\left(3a^6x^6+27a^6x^4+33a^6x2+a^6+72a^5x^5+24a^5x^3+72a^{5x}+27a^4x^6+459a^4x^4+441a^4x^2+33a^4+240a^3x^5+800a^3x^3+240a^3x+33a^2x^6+441a^2x^4+459x^2a^2+27a^2+75ax^5+240ax^3+72ax+x^6+33x^4+27x^2+3\right)}{\left(a^2+3\right)\left(a^6+33a^4+27a^{2+3}\right)\left(x^{2+3}\right)\left(x^6+33x^4+27x^2+3\right)}=0\)
mấy nhân tử sau ko cần chú ý đâu :)) chỉ cần chú ý đến x+a=0 <=>x=-a thôi :))
bài này đúng 100% nhé chỉ sợ gõ sai thôi, ko tin có thể dùng máy tính kiểm tra
Đúng 0
Bình luận (0)
a) Trong Hình 5, M là điểm biểu diễn của góc lượng giác α trên đường tròn lượng giác. Giải thích vì sao {sin ^2}alpha + {cos ^2}alpha 1b) Chia cả hai vế của biểu thức ở câu a) cho {cos ^2}alpha ta được đẳng thức nào?c) Chia cả hai vế của biểu thức ở câu a) cho {sin ^2}alpha ta được đẳng thức nào?
Đọc tiếp
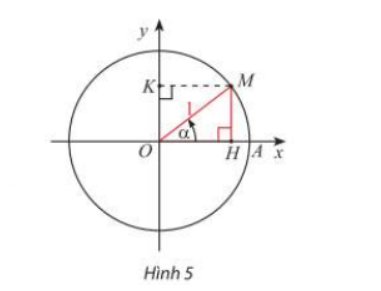
a) Trong Hình 5, M là điểm biểu diễn của góc lượng giác α trên đường tròn lượng giác. Giải thích vì sao \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
b) Chia cả hai vế của biểu thức ở câu a) cho \({\cos ^2}\alpha \) ta được đẳng thức nào?
c) Chia cả hai vế của biểu thức ở câu a) cho \({\sin ^2}\alpha \) ta được đẳng thức nào?
a) Do \(\begin{array}{l}\sin \alpha = MH \Rightarrow {\sin ^2}\alpha = M{H^2}\\\cos \alpha = OH \Rightarrow {\cos ^2}\alpha = O{H^2}\end{array}\)
Áp dụng định lý Py – Ta – Go vào tam giác OMH vuông tại H ta có:
\(\begin{array}{l}M{H^2} + O{H^2} = O{M^2} = 1\\ \Rightarrow {\sin ^2}\alpha + {\cos ^2}\alpha = 1\end{array}\)
b) Chia cả hai vế cho \({\cos ^2}\alpha \), ta được:
\(\begin{array}{l}\frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\\ \Leftrightarrow {\tan ^2}\alpha + 1 = \frac{1}{{{{\cos }^2}\alpha }}\end{array}\)
c) Chia cả hai vế cho \({\sin ^2}\alpha \), ta được:
\(\begin{array}{l}\frac{{{{\sin }^2}\alpha }}{{{{\sin }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\\ \Leftrightarrow {\cot ^2}\alpha + 1 = \frac{1}{{{{\sin }^2}\alpha }}\end{array}\)
Đúng 0
Bình luận (0)
Cho 0<α<π va α≠\(\dfrac{\pi}{2}\). Chung minh rang
\(\sqrt{1+cos\alpha}\) + \(\sqrt{1-cos\alpha}\) = 2sin\((\dfrac{\alpha}{2}+\dfrac{\pi}{4}\))
Bài 1: Cho đường thẳng d : (1 - m2)x + 2my + m2 - 4m + 1 0. Viết phương trình đường tròn (C) luôn tiếp xúc với d với mọi m.
Bài 2: Cho (Cα) : (x2 + y2)sin α 2( x cos α + y sin α - cos α) (α ≠ k π)
a, CMR: (Cα) luôn là một đường tròn. Định tâm và bán kính của (Cα).
b, CMR: (Cα) có một tiếp tuyến cố định mà ta sẽ xác định phương trình.
Bài 3: Biện luận tùy theo m sự tương giao của đường thẳng (△) và đường tròn (C).
a, (C): x2 + y2 + 2x - 4y + 4 0 và (△): mx - y + 2 0.
b, (C): x2 + y2 - 4...
Đọc tiếp
Bài 1: Cho đường thẳng d : (1 - m2)x + 2my + m2 - 4m + 1 = 0. Viết phương trình đường tròn (C) luôn tiếp xúc với d với mọi m.
Bài 2: Cho (Cα) : (x2 + y2)sin α = 2( x cos α + y sin α - cos α) (α ≠ k π)
a, CMR: (Cα) luôn là một đường tròn. Định tâm và bán kính của (Cα).
b, CMR: (Cα) có một tiếp tuyến cố định mà ta sẽ xác định phương trình.
Bài 3: Biện luận tùy theo m sự tương giao của đường thẳng (△) và đường tròn (C).
a, (C): x2 + y2 + 2x - 4y + 4 = 0 và (△): mx - y + 2 = 0.
b, (C): x2 + y2 - 4x + 6y + 3 = 0 và (△): 3x - y + m = 0.
Bài 4: Cho đường tròn (C): x2 + y2 - 2x - 4y - 4 = 0 và (C'): x2 + y2 + 6x - 2y + 1 = 0.
a, Chứng minh (C) và (C') cắt nhau tại hai điểm A, B.
b, Cho điểm M(4;1). Chứng minh qua M có hai tiếp tuyến đến (C). Gọi E, F là hai tiếp điểm của hai tiếp tuyến trên với (C). Hãy lập phương trình đường tròn (C) ngoại tiếp với △ MEF.






















