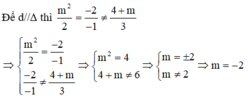Chuyển đường thẳng d: 2x-y+1=0 sang dạng tham số

Những câu hỏi liên quan
Trong mặt phẳng Oxy cho ba điểm A(-6;3), B(0;-1), C(3;2) a) Viết phương trình tham số với đường thẳng AB b) Viết phương trình đường thẳng d đi qua C và vuông góc với đường thẳng AB c) Tìm tọa độ điểm m trên đường thẳng d 2x- y + 3 = 0 sao cho | vectơ MA + vectơ MB + MC| nhỏ nhất
Trong mặt phẳng Oxy cho ba điểm A(-6;3), B(0;-1), C(3;2) a) Viết phương trình tham số với đường thẳng AB b) Viết phương trình đường thẳng d đi qua C và vuông góc với đường thẳng AB c) Tìm tọa độ điểm m trên đường thẳng d 2x- y + 3 = 0 sao cho | vectơ MA + vectơ MB + MC| nhỏ nhất
a: vecto AB=(6;-4)
PTTS là:
x=-6+6t và y=3-4t
b: Vì (d) vuông góc AB nên (d) có VTPT là (3;-2)
Phương trình(d) là:
3(x-3)+(-2)(y-2)=0
=>3x-9-2y+4=0
=>3x-2y-5=0
Đúng 0
Bình luận (0)
Phương trình nào sau đây là phương trình tham số của đường thẳng?
A. \(2x - y + 1 = 0\)
B. \(\left\{ \begin{array}{l}x = 2t\\y = t\end{array} \right.\)
C. \({x^2} + {y^2} = 1\)
D. \(y = 2x + 3\)
Cho đường thẳng d: x - 2y + 1 = 0. Viết phương trình đường thẳng d dưới dạng chính tắc và tham số.
Ta có: \(d\) có 1 vec-tơ pháp tuyến \(\overrightarrow{n}\left(1;-2\right)\). Suy ra, \(d\) có 1 vec-tơ chỉ phương \(\overrightarrow{u}\left(2;1\right)\).
Ta có: \(d\) qua \(M\left(-1;0\right)\).
Vậy, phương trình tham số của \(d:\left\{\begin{matrix}x=-1+2t\\y=t\end{matrix}\right.\)
Phương trình chính tắc của \(d:\frac{x+1}{2}=\frac{y}{1}\)
Đúng 0
Bình luận (3)
Cho A(1;-3;2) và mặt phẳng (P):2x-y+3z-10. Viết phương trình tham số đường thẳng d đi qua A, vuông góc với (P). A.
x
2
+
t
y
-
1
-...
Đọc tiếp
Cho A(1;-3;2) và mặt phẳng (P):2x-y+3z-1=0. Viết phương trình tham số đường thẳng d đi qua A, vuông góc với (P).
A. x = 2 + t y = - 1 - 3 t z = 3 + 2 t
B. x = 1 + 2 t y = - 3 + t z = 2 + 3 t
C. x = 1 + 2 t y = - 3 - t z = 2 + 3 t
D. x = 1 + 2 t y = - 3 - t z = 2 - 3 t
Cho mặt phẳng
α
:
4
x
+
y
+
2
z
+
1
0
và
β
:
2
x
-
2
y
+
z
+
3
0
. Viết phương trình tham số của đường thẳng d là giao của (α) và (β). A.
x...
Đọc tiếp
Cho mặt phẳng α : 4 x + y + 2 z + 1 = 0 và β : 2 x - 2 y + z + 3 = 0 . Viết phương trình tham số của đường thẳng d là giao của (α) và (β).
A. x = t y = 1 - t z = - 1 - 2 t
B. x = t y = 1 z = - 1 - 2 t
C. x = - t y = 1 z = - 1 - 2 t
D. x = - t y = 1 + t z = - 1 - 2 t
Cho mặt phẳng
(
α
)
:
4
x
+
y
+
2
z
+
1
0
và
(
β
)
:
2
x
-
2
y
+
z
-
3
0
. Viết phương trình tham số của đường thẳng d là giao của
α
và
β
Đọc tiếp
Cho mặt phẳng ( α ) : 4 x + y + 2 z + 1 = 0 và ( β ) : 2 x - 2 y + z - 3 = 0 . Viết phương trình tham số của đường thẳng d là giao của α và β
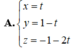
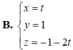
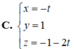
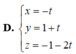
Tìm giá trị thực của tham số m để đường thẳng d: y2x+m tiếp xúc với parabol P: ym−1x2+2mx+3m−1.A.m−1.B.m0.C.m2. D.m1.
Đọc tiếp
Tìm giá trị thực của tham số m để đường thẳng d: y=2x+m tiếp xúc với parabol P: y=m−1x2+2mx+3m−1.
A.m=−1.
B.m=0.
C.m=2.
D.m=1.
Tìm tham số m để hai đường thẳng d: m 2 x - 2y + 4 + m = 0 và Δ: 2x - y + 3 = 0 song song với nhau.
A. m = 4
B. m = 2
C. m = -2
D. m = 2 va m = -2