\(\Leftrightarrow5\left(\frac{9^x}{25^x}\right)+2\left(\frac{15^x}{25^x}\right)-3\ge0\)

\(\Leftrightarrow5\left(\frac{3}{5}\right)^x+2\left(\frac{3}{5}\right)^x-3\ge0\)

\(\Leftrightarrow\left[5\left(\frac{3}{5}\right)^x-3\right]\left[\left(\frac{3}{5}\right)^x+1\right]\ge0\)

\(\Leftrightarrow5\left(\frac{3}{5}\right)^x-3\ge0\)

\(\Leftrightarrow\left(\frac{3}{5}\right)^x\ge\frac{3}{5}\)

\(\Rightarrow x\ge1\)

Đáp án B

Chọn D

Ta có: \(x-1=0\Rightarrow x=1\),\(x+3=0 \Rightarrow x = - 3\)

BXD:

Vậy \(T=(-\infty;-3]\cup[1;+\infty)\)

- Đặt \(f\left(x\right)=\left(x-1\right)\left(x+3\right)\)

- Cho \(f\left(x\right)=0\Rightarrow\left\{{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)

- Lập bảng xét dấu : 

x___________-3_________________1______________

x-1____-_____|________-_________0______+___________

x+3___-______0_______+_________|_____+____________

f(x)___+______0_______-__________0_____+____________

- Từ bảng xét dấu :- Để f(x) \(\ge0\)

Vậy phương trình có tập nghiệm \((-\infty;-3]\cup[1;+\infty)\)

\(\log_{\dfrac{1}{4}}x>-2\\ \Rightarrow\left\{{}\begin{matrix}x>0\\\log_{\dfrac{1}{4}}x>\log_{\dfrac{1}{4}}16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x>0\\x< 16\end{matrix}\right.\\ \Leftrightarrow0< x< 16\)

Chọn C.

Đặt \(f\left(x\right)=\dfrac{x-1}{\left(x-2\right)\left(x-3\right)}.\)

 \(x-1=0.\Leftrightarrow x=1.\\ x-2=0.\Leftrightarrow x=2.\\ x-3=0.\Leftrightarrow x=3.\)

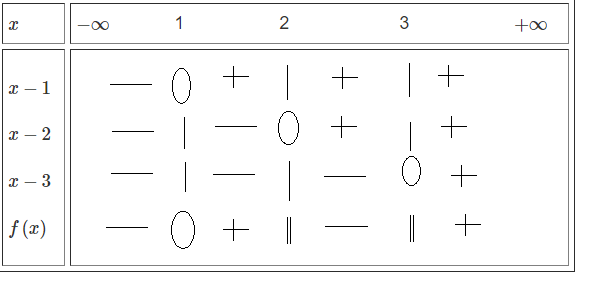
\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\) \(\left(1;2\right)\cup\left(3;+\infty\right).\)

\(\Rightarrow B.\)

b

- Với \(m=\dfrac{1}{2}\) ko thỏa mãn

- Với \(m\ne\dfrac{1}{2}\)

\(\Leftrightarrow\left(2m-1\right)x^3-\left(2m-1\right)x^2-\left(m-2\right)x^2+\left(m-4\right)x+2\ge0\)

\(\Leftrightarrow\left(2m-1\right)x^2\left(x-1\right)-\left(x-1\right)\left[\left(m-2\right)x+2\right]\ge0\)

\(\Leftrightarrow\left(x-1\right)\left[\left(2m-1\right)x^2-\left(m-2\right)x-2\right]\ge0\) (1)

Do (1) luôn chứa 1 nghiệm \(x=1\in\left(0;+\infty\right)\) nên để bài toán thỏa mãn thì cần 2 điều sau đồng thời xảy ra:

+/ \(2m-1>0\Rightarrow m>\dfrac{1}{2}\)

+/ \(\left(2m-1\right)x^2-\left(m-2\right)x-2=0\) có 2 nghiệm trong đó \(x_1\le0\) và \(x_2=1\)

Thay \(x=1\) vào ta được:

\(\left(2m-1\right)-\left(m-2\right)-2=0\Leftrightarrow m=1\)

Khi đó: \(x^2+x-2=0\) có 2 nghiệm \(\left[{}\begin{matrix}x_1=-2< 0\left(thỏa\right)\\x_2=1\end{matrix}\right.\)

Vậy \(m=1\)

\(0,5^{3x-1}>0,25\)

\(\Leftrightarrow0,5^{3x-1}>0,5^2\)

\(\Leftrightarrow3x-1< 2\)

\(\Leftrightarrow3x< 3\)

\(\Leftrightarrow x< \dfrac{3}{3}\)

\(\Leftrightarrow x< 1\)

Vậy: \(\left(-\infty;1\right)\)

Chọn A

a) Ta có: \(2x + 3 \ge 0 \Leftrightarrow x \ge \frac{{ - 3}}{2}\)

\( \Rightarrow \) Tập hợp E là: \(E = \left\{ {x \in \mathbb{R}|x \ge \frac{{ - 3}}{2}} \right\}\)

và \( - x + 5 \ge 0 \Leftrightarrow x \le 5\)

\( \Rightarrow \) Tập hợp G là \(G = \left\{ {x \in \mathbb{R}|x \le 5} \right\}\)

\( \Rightarrow E \cap G = \){\(x \in \mathbb{R}|\)\(x \ge \frac{{ - 3}}{2}\) và \(x \le 5\)} \( = \left\{ {x \in \mathbb{R}|\frac{{ - 3}}{2} \le x \le 5} \right\}\)

Vậy tập hợp D \( = \left\{ {x \in \mathbb{R}|\frac{{ - 3}}{2} \le x \le 5} \right\} = [\frac{{ - 3}}{2}; 5]\)

b) Ta có: \(x + 2 > 0 \Leftrightarrow x>-2\)

\( \Rightarrow E = \left\{ {x \in \mathbb{R}|x >-2 }\right\}\)

và \( 2x - 9 < 0 \Leftrightarrow x < \frac{9}{2}\)

\( \Rightarrow G = \left\{ {x \in \mathbb{R}|x < \frac{9}{2}} \right\}\)

\( \Rightarrow E \cap G = \){\(x \in \mathbb{R}|\)\(x > -2 \) và \(x < \frac{9}{2}\)} \( = \left\{ {x \in \mathbb{R}|-2<x< {9\over 2} } \right\}\)

Vậy \( D= \left\{ {x \in \mathbb{R}|-2<x< {9\over 2}} \right\}=(-2;{9\over 2})\)

Chọn B

B nhá bạn 

B