Với điều kiện alpha khác kpi và alpha khác pi/2 + kpi, chứng minh rằng |tan a + cot a| > bằng 2
mọi người giúp em với ạ, em xin lỗi vì không viết được các dấu ra TT
Chứng minh đẳng thức :
sin2α.tanα + cos2α.cotα+2sinα.cosα = tanα+cotα
Mọi người giúp em với ạ !!
Mình viết luôn là sin với cos, bạn tự cho thêm \(\alpha\) nhé.
VT= \(\sin^2.\dfrac{\sin}{\cos}+\cos^2.\dfrac{\cos}{\sin}+2\sin\cos\)
= \(\dfrac{\sin^3}{\cos}+\dfrac{\cos^3}{\sin}+2\sin\cos\)
= \(\dfrac{\sin^4+\cos^4+2\sin^2.\cos^2}{\cos.\sin}\)
= \(\dfrac{\left(\sin^2+\cos^2\right)^2}{\cos.\sin}\)
= \(\dfrac{1}{\sin.\cos}\)(1)
VP = \(\dfrac{\sin}{\cos}+\dfrac{\cos}{\sin}\)
= \(\dfrac{\sin^2+\cos^2}{\cos.\sin}\)
= \(\dfrac{1}{\cos.\sin}\)(2)
từ (1) và (2) => VT=VP (đpcm)
Chúc bạn học tốt!
Chứng minh rằng với mọi \(\alpha\), ta luôn có :
a) \(\sin\left(\alpha+\dfrac{\pi}{2}\right)=\cos\alpha\)
b) \(\cos\left(\alpha+\dfrac{\pi}{2}\right)=-\sin\alpha\)
c) \(\tan\left(\alpha+\dfrac{\pi}{2}\right)=-\cot\alpha\)
d) \(\cot\left(\alpha+\dfrac{\pi}{2}\right)=-\tan\alpha\)
a)\(sin\left(\alpha+\dfrac{\pi}{2}\right)=cos\left[\dfrac{\pi}{2}-\left(\alpha+\dfrac{\pi}{2}\right)\right]=cos\left(-\alpha\right)=cos\alpha\).
b) \(cos\left(x+\dfrac{\pi}{2}\right)=sin\left[\dfrac{\pi}{2}-\left(x+\dfrac{\pi}{2}\right)\right]=sin\left(-x\right)=-sinx\).
c) \(tan\left(\alpha+\dfrac{\pi}{2}\right)=\dfrac{sin\left(\alpha+\dfrac{\pi}{2}\right)}{cos\left(\alpha+\dfrac{\pi}{2}\right)}=\dfrac{cos\alpha}{-sin\alpha}=-cot\alpha\).
d) \(cot\left(\alpha+\dfrac{\pi}{2}\right)=\dfrac{cos\left(\alpha+\dfrac{\pi}{2}\right)}{sin\left(\alpha+\dfrac{\pi}{2}\right)}=\dfrac{-sin\alpha}{cos\alpha}=-tan\alpha\).
câu 29 : Nghiệm của pt cotx=-căn 3 trên 3 ?
câu 30 nghiệm của phương trình cot(x+pi/3)= căn 3 có dạng x = -pi/n -kpi/m (k thuộc z ) . khi đó n-m bằng ?
câu 31 phương trình cot (2x + pi/6) =1 có họ nghiệm dạng x =alpha + kpi/2 (k thuoc z):alpha thuoc (0 :pi/2) khi đó giá trị gần nhất của m là bnh ?>
Chứng minh rằng:
\(cot\dfrac{\alpha}{2}.cot\dfrac{\beta}{2}=2\) với \(sin\alpha+sin\beta=3sin\left(\alpha+\beta\right),\alpha+\beta\ne k2\pi\)
Bài 1:
1. Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào góc \(\alpha\)( Với \(\alpha\)là góc nhọn)
\(\left(\tan\alpha+\cot\alpha\right)^2-\left(\tan\alpha-\cot\alpha\right)^2\)
2. So sánh \(\frac{2-\sqrt{2+\sqrt{2+\sqrt{2}}}}{2-\sqrt{2+\sqrt{2}}}\)và \(\frac{1}{4}\)
(Giúp em câu này nữa thôi ạ)
1) \(\left(\tan\alpha+\cot\alpha\right)^2-\left(\tan\alpha-\cot\alpha\right)^2\)
= \(\tan^2\alpha+\cot^2\alpha+2\tan\alpha.\cot\alpha-\tan^2\alpha+2\tan\alpha.\cot\alpha-\cot^2\alpha\)
= \(4\tan\alpha.\cot\alpha\)
= \(4.\frac{\cos\alpha}{\sin\alpha}.\frac{\sin\alpha}{\cos\alpha}=4\)
2) \(\frac{2-\sqrt{2+\sqrt{2+\sqrt{2}}}}{2-\sqrt{2+\sqrt{2}}}\)
= \(\frac{4-2-\sqrt{2+\sqrt{2}}}{\left(2+\sqrt{2+\sqrt{2+\sqrt{2}}}\right)\left(2-\sqrt{2+\sqrt{2}}\right)}\)
= \(\frac{1}{\left(2+\sqrt{2+\sqrt{2+\sqrt{2}}}\right)}\)
Mặt khác: \(\sqrt{2}< 2\Rightarrow2+\sqrt{2}< 4\Rightarrow2+\sqrt{2+\sqrt{2}}< 2+\sqrt{4}=4\)
=> \(2+\sqrt{2+\sqrt{2+\sqrt{2}}}< 2+\sqrt{4}=4\)
=> \(\frac{1}{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}>\frac{1}{4}\)
=> \(\frac{2-\sqrt{2+\sqrt{2+\sqrt{2}}}}{2-\sqrt{2+\sqrt{2}}}>\frac{1}{4}\)
Chứng minh rằng với mọi góc \(\alpha \;\;({0^o} \le \alpha \le {180^o})\), ta đều có:
a) \({\cos ^2}\alpha + {\sin ^2}\alpha = 1\)
b) \(\tan \alpha .\cot \alpha = 1\;({0^o} < \alpha < {180^o},\alpha \ne {90^o})\)
c) \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\;(\alpha \ne {90^o})\)
d) \(1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\;({0^o} < \alpha < {180^o})\)
a)
Trên nửa đường tròn đơn vị, lấy điểm M sao cho \(\widehat {xOM} = \alpha \)
Gọi H, K lần lượt là các hình chiếu vuông góc của M trên Ox, Oy.
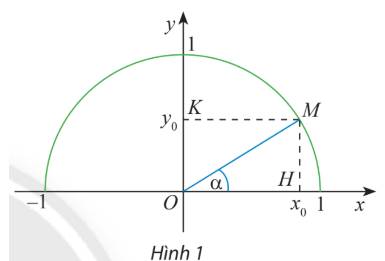
Ta có: tam giác vuông OHM vuông tại H và \(\alpha = \widehat {xOM}\)
Do đó: \(\sin \alpha = \frac{{MH}}{{OM}} = MH;\;\cos \alpha = \frac{{OH}}{{OM}} = OH.\)
\( \Rightarrow {\cos ^2}\alpha + {\sin ^2}\alpha = O{H^2} + M{H^2} = O{M^2} = 1\)
b) Ta có:
\(\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}.\\ \Rightarrow \;\tan \alpha .\cot \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{\cos \alpha }}{{\sin \alpha }} = 1\end{array}\)
c) Với \(\alpha \ne {90^o}\) ta có:
\(\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\\ \Rightarrow \;1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\;\end{array}\)
d) Ta có:
\(\begin{array}{l}\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }};\;\\ \Rightarrow \;1 + {\cot ^2}\alpha = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\;\end{array}\)
Câu2: Trong ∆ vuông với góc alpha tùy ý. Chứng minh : tan alpha × cos alpha = 1.!! ( mọi người giúp em với )
a) tính các giá trị lượng giác của góc alpha biết
1. cos \(\alpha\) = \(\dfrac{-2}{\sqrt{5}}\) và \(\dfrac{-\pi}{2}\)< \(\alpha\) < 0
2. tan \(\alpha\) = - 2 và \(\dfrac{\pi}{2}\)< \(\alpha\) < \(\pi\)
3. cot \(\alpha\) = 3 và \(\pi\) < \(\alpha\) < \(\dfrac{3\pi}{2}\)
b)
1. Cho tan x = - 2 và 90° < x < 180°. Tính A = \(\dfrac{2\sin x+\cos x}{\cos x-3\sin x}\)
2. Cho tan x = - 2 . Tính B = \(\dfrac{2\sin x+3\cos x}{3\sin x-2\cos x}\)
a:
2: pi/2<a<pi
=>sin a>0 và cosa<0
tan a=-2
1+tan^2a=1/cos^2a=1+4=5
=>cos^2a=1/5
=>\(cosa=-\dfrac{1}{\sqrt{5}}\)
\(sina=\sqrt{1-\dfrac{1}{5}}=\dfrac{2}{\sqrt{5}}\)
cot a=1/tan a=-1/2
3: pi<a<3/2pi
=>cosa<0; sin a<0
1+cot^2a=1/sin^2a
=>1/sin^2a=1+9=10
=>sin^2a=1/10
=>\(sina=-\dfrac{1}{\sqrt{10}}\)
\(cosa=-\dfrac{3}{\sqrt{10}}\)
tan a=1:cota=1/3
b;
tan x=-2
=>sin x=-2*cosx
\(A=\dfrac{2\cdot sinx+cosx}{cosx-3sinx}\)
\(=\dfrac{-4cosx+cosx}{cosx+6cosx}=\dfrac{-3}{7}\)
2: tan x=-2
=>sin x=-2*cosx
\(B=\dfrac{-4cosx+3cosx}{-6cosx-2cosx}=\dfrac{1}{8}\)
a) tính các giá trị lượng giác của góc alpha biết
1. cos \(\alpha\) = \(\dfrac{-2}{\sqrt{5}}\) và \(\dfrac{-\pi}{2}\)< \(\alpha\) < 0
2. tan \(\alpha\) = - 2 và \(\dfrac{\pi}{2}\)< \(\alpha\) < \(\pi\)
3. cot \(\alpha\) = 3 và \(\pi\) < \(\alpha\) < \(\dfrac{3\pi}{2}\)
b)
1. Cho tan x = - 2 và 90° < x < 180°. Tính A = \(\dfrac{2\sin x+\cos x}{\cos x-3\sin x}\)
2. Cho tan x = - 2 . Tính B = \(\dfrac{2\sin x+3\cos x}{3\sin x-2\cos x}\)