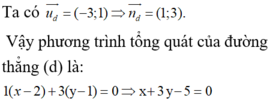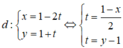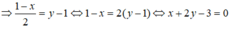Chỉ mình cách chuyển phương trình tham số sang pt tổng quát của đường thẳng. Có ví dụ nha!

Những câu hỏi liên quan
Bài tập 1: Cho đường thẳng đi qua điểm và có vectơ pháp tuyến . Viết phương trình tham số và phương trình tổng quát của đường thẳng .Bài tập 2: Cho tam giác ABC có . a) Viết phương trình tổng quát của cạnh BC. b) Viết phương trình tham số của đường t...
Xem chi tiết
Trong mặt phẳng Oxy cho A (4;1), B (-2;3), C (5;-1). a) Viết phương trình tham số và trình tổng quát của đường thẳng đi qua hai điểm A,C b) Viết phương trình tham số và trình tổng quát của đường thẳng A và vuông góc với B,C c) Viết phương trình tham số và trình tổng quát của đường thẳng qua A và song song với đường thẳng d : 2x - y + 3 = 0
Đường thẳng (d) có phương trình tham số:
x
2
-
3
t
y
1
+
t
Phương trình tổng quát của đường thẳng (d) là A. x+3y+50 B. -3x+y-70 C. -3x+y+50 D. x+3y-50
Đọc tiếp
Đường thẳng (d) có phương trình tham số: x = 2 - 3 t y = 1 + t Phương trình tổng quát của đường thẳng (d) là
A. x+3y+5=0
B. -3x+y-7=0
C. -3x+y+5=0
D. x+3y-5=0
cho tam giác ABC có A(-1;0) B(1;2) C(3;2) a, Viết phương trình tham số và phương trình tổng quát của đường thẳng AB b,Viết phương trình tổng quát của đường cao AH của tam giác ABC c, Viết phương trình tham số của trung tuyến BM ( với M là trung điểm AC) d, Viết phương trình tổng quát đường trung trực của đoạn AC e, Tìm điểm D thuộc đoạn AB sao cho CD=5
a: vecto AB=(2;2)=(1;1)
=>VTPT là (-1;1)
Phương trình tham số AB là: \(\left\{{}\begin{matrix}x=-1+t\\y=0+t=t\end{matrix}\right.\)
Phương trình tổng quát của AB là:
-1(x+1)+1(y-0)=0
=>-x-1+y=0
=>x-y+1=0
b: vecto BC=(2;0)
Vì AH vuông góc BC
nên AH nhận vecto BC làm vtpt và đi qua A
=>AH: 2(x+1)+0(y-0)=0
=>2x+2=0
=>x=-1
c: Tọa độ M la:
x=(-1+3)/2=2/2=1 và y=(0+2)/2=1
B(1;2); M(1;1)
vecto BM=(0;-1)
=>VTPT là (1;0)
Phương trình BM là:
1(x-1)+0(y-2)=0
=>x-1=0
=>x=1
Đúng 1
Bình luận (1)
Cho đường thẳng ∆ có phương trình tổng quát là 2x – y – 2 0. Phương trình nào sau đây là phương trình tham số của ∆? A.
x
3
+
2
t
y
4
−
t
B....
Đọc tiếp
Cho đường thẳng ∆ có phương trình tổng quát là 2x – y – 2 = 0. Phương trình nào sau đây là phương trình tham số của ∆?
A. x = 3 + 2 t y = 4 − t
B. x = 1 + 2 t y = − 1 + 4 t
C. x = 3 + 4 t y = 1 − 2 t
D. x = 3 + t y = 4 + 2 t
ĐÁP ÁN D
Đường thẳng ∆ có vectơ pháp tuyến n → = 2 ; − 1 ⇒ ∆ có vectơ chỉ phương là u → = 1 ; 2 hoặc các vectơ khác vectơ – không mà cùng phương với nó.
Ta chỉ quan tâm đến phương án B và D. Kiểm tra tiếp hai điểm M 1 3 ; 4 , M 2 1 ; − 1 xem điểm nào nằm trên ∆. Ta có M 1 ∈ ∆ , M 2 ∉ ∆
Vậy phương trình tham số của đường thẳng ∆: x = 3 + t y = 4 + 2 t
Chú ý. Do phương trình tham số của đường thẳng là không duy nhất nên ta sẽ đi kiểm tra các phương án trả lời được đưa ra thay cho việc tiến hành viết phương trình tham số của đường thẳng.
Đúng 0
Bình luận (0)
Cho đường thẳng ∆ có phương trình tham số là
x
−
1
+
4
t
y
3
−
2
t
. Phương trình n...
Đọc tiếp
Cho đường thẳng ∆ có phương trình tham số là x = − 1 + 4 t y = 3 − 2 t . Phương trình nào sau đây là phương trình tổng quát của ∆?
A.x – 2y + 5 = 0
B.x + 2y – 11 = 0
C.x + 2y – 5 = 0
D.x – y = 0
ĐÁP ÁN C
Đường thẳng ∆ đi qua M(-1; 3) và có vectơ chỉ phương u → = 4 ; − 2 ⇒ vectơ pháp tuyến n → = 1 ; 2 nên phương trình tổng quát của ∆ là :
(x + 1) + 2(y – 3) = 0 ⟺ x + 2y – 5 = 0.
Đúng 0
Bình luận (0)
cho đường thẳng △ có phương trình tham số: \(\left\{{}\begin{matrix}x=1+2t\\y=-3-t\end{matrix}\right.\)
a) viết phương trình tổng quát của đg thẳng △
b) cho đg thẳng d1: x+2y-8=0 và d2: x-2y=0. viết phương trình tổng quát của đg thẳng đi qua giao điểm của d1 với d2 và vuông góc với △
giúp mk vs ạ mk cần gấp
a: Δ có vtcp là (2;-1) và đi qua A(1;-3)
=>VTPT là (1;2)
PTTQ là:
1(x-1)+2(y+3)=0
=>x-1+2y+6=0
=>x+2y+5=0
b: Vì d vuông góc Δ nên d: 2x-y+c=0
Tọa độ giao của d1 và d2 là:
x+2y=8 và x-2y=0
=>x=4 và y=2
Thay x=4 và y=2 vào 2x-y+c=0, ta được
c+2*4-2=0
=>c=-2
Đúng 0
Bình luận (0)
Lập phương trình tham số và phương trình tổng quát của đường thẳng d trong mỗi trường hợp sau:
a) d đi qua điểm \(A( - 1;5)\) và có vectơ chỉ phương \(\overrightarrow u = (2;1)\)
b) d đi qua điểm \(B(4; - 2)\) và có vectơ pháp tuyến là \(\overrightarrow n = (3; - 2)\)
c) d đi qua \(P(1;1)\) và có hệ số góc \(k = - 2\)
d) d đi qua hai điểm \(Q(3;0)\)và \(R(0;2)\)
a) Đường thẳng \(d\) đi qua điểm \(A( - 1;5)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {2;1} \right)\), nên có phương trình tham số là:
\(\left\{ \begin{array}{l}x = - 1 + 2t\\y = 5 + t\end{array} \right.\)
Đường thẳng \(d\) có vectơ chỉ phương \(\overrightarrow u = \left( {2;1} \right)\),nên có vectơ pháp tuyền là \(\overrightarrow n = \left( {1; - 2} \right)\) và đi qua \(A( - 1;5)\)
Ta có phương trình tổng quát là
\((x + 1) - 2(y - 5) = 0 \Leftrightarrow x - 2y + 11 = 0\)
b) Đường thẳng \(d\) có vectơ pháp tuyến \(\overrightarrow n = \left( {3; - 2} \right)\) nên có vectơ chỉ phương \(\overrightarrow u = \left( {2;3} \right)\), và đi qua điểm \(B(4; - 2)\) nên ta có phương trình tham số của \(d\) là :
\(\left\{ \begin{array}{l}x = 4 + 2t\\y = - 2 + 3t\end{array} \right.\)
Đường thẳng \(d\) đi qua điểm \(B(4; - 2)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {3; - 2} \right)\)
Phương trình tổng quát của đường thẳng d là:
\(3(x - 4) - 2(y + 2) = 0 \Leftrightarrow 3x - 2y - 16 = 0\)
c) Đường thẳng \(d\) có dạng \(y = ax + b\)
d đi qua \(P(1;1)\) và có hệ số góc \(k = - 2\) nên ta có:
\(1 = - 2.1 + b \Rightarrow b = 3\)
Suy ra đồ thị đường thẳng d có dạng \(y = - 2x + 3\)
Vậy đường thẳng d có phương trình tổng quát là \(y + 2x - 3 = 0\)
Suy ra đường thẳng d có vectơ pháp tuyến \(\overrightarrow n = \left( {2;1} \right)\), nên có vectơ chỉ phương là \(\overrightarrow u = \left( {1; - 2} \right)\) và đi qua điểm \(P(1;1)\) nên ta có phương trình tham số của d là :
\(\left\{ \begin{array}{l}x = 1 + t\\y = 1 - 2t\end{array} \right.\)
d) Đường thẳng \(d\) đi qua hai điểm \(Q(3;0)\)và \(R(0;2)\) nên có vectơ chỉ phương \(\overrightarrow u = \overrightarrow {QR} = ( - 3;2)\) và có vectơ pháp tuyến \(\overrightarrow n = (2;3)\)
Phương trình tham số của \(\Delta \) là: \(\left\{ \begin{array}{l}x = 3 - 3t\\y = 2t\end{array} \right.\)
Phương trình tổng quát của \(\Delta \) là: \(2(x - 3) + 3(x - 0) = \Leftrightarrow 2x + 3y - 6 = 0\)
Đúng 0
Bình luận (0)
Cho phương trình tham số của đường thẳng
d
:
x
1
-
2
t
y
1
+
t
. Phương trình tổng quát của d là: A. x + 2y - 3 0 B. x - 2y - 3 0 C. x -...
Đọc tiếp
Cho phương trình tham số của đường thẳng d : x = 1 - 2 t y = 1 + t . Phương trình tổng quát của d là:
A. x + 2y - 3 = 0
B. x - 2y - 3 = 0
C. x - 2y + 3 = 0
D. x + 2y + 3 = 0