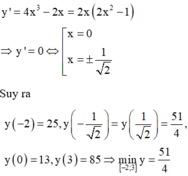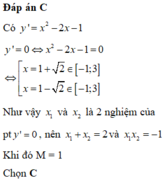Giá trị nhỏ nhất của C=(x2+13)2

Những câu hỏi liên quan
Câu 18: Giá trị nhỏ nhất của biểu thức x2 – 6x + 13 làA. 3 B. 4 C. -3 D. -4 Câu 19 : Giá trị lớn nhất của biểu thức -x2 +4x - 7 làA. 3 B. 4 C. -3 D. 5 Câu 20: Điền vào chỗ trống 4x2 + 4x – y2 + 1 (…)(2x + y + 1): A. 2x + y + 1 B. 2x – y + 1 C....
Đọc tiếp
Câu 18: Giá trị nhỏ nhất của biểu thức x2 – 6x + 13 là
A. 3 B. 4 C. -3 D. -4
Câu 19 : Giá trị lớn nhất của biểu thức -x2 +4x - 7 là
A. 3 B. 4 C. -3 D. 5
Câu 20: Điền vào chỗ trống 4x2 + 4x – y2 + 1 = (…)(2x + y + 1):
A. 2x + y + 1 B. 2x – y + 1
C. 2x – y D. 2x + y
Tìm giá trị nhỏ nhất của hàm số
y
x
4
-
x
2
+
13
trên đoạn
-
2
;
3
. A.
m
13
B.
m
13
C.
m
49
4
D.
m...
Đọc tiếp
Tìm giá trị nhỏ nhất của hàm số y = x 4 - x 2 + 13 trên đoạn - 2 ; 3 .
A. m = 13
B. m = 13
C. m = 49 4
D. m = 51 4
Ta có:
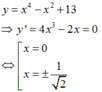
Hàm số đã cho liên tục trên - 2 ; 3 và
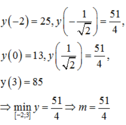
Chọn: D
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của hàm số
y
x
4
−
x
2
+
13
trên đoạn [-2;3] A.
m
51
4
B.
m
51
2
C.
m
13
D.
m
49
4
Đọc tiếp
Tìm giá trị nhỏ nhất của hàm số y = x 4 − x 2 + 13 trên đoạn [-2;3]
A. m = 51 4
B. m = 51 2
C. m = 13
D. m = 49 4
Đáp án A
Xét hàm số y = x 4 − x 2 + 13 trên [-2;3] có y ' = 4 x 3 − 2 x ; y ' = 0 ⇔ x = 0 x = ± 2 2
Tính y − 2 = 25 ; y ± 2 2 = 51 4 ; y 0 = 13 ; y 3 = 85. Vậy m = min − 2 ; 3 y = 51 4
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của hàm số
y
x
4
−
x
2
+
13
trên đoạn
−
2
;
3
A.
51
4
B.
51
2
C.
49
4
D. 13
Đọc tiếp
Tìm giá trị nhỏ nhất của hàm số y = x 4 − x 2 + 13 trên đoạn − 2 ; 3
A. 51 4
B. 51 2
C. 49 4
D. 13
Giá trị nhỏ nhất của hàm số y = x 4 - x 2 + 13 trên đoạn [−1;2] bằng
A. 85.
B. 12,75.
C. 25.
D. 13.
*Các em nên MODE 7 trên đoạn [−1;2].
Chọn đáp án B.
Đúng 0
Bình luận (0)
Hàm số
y
x
3
3
-
x
2
-
x
đạt giá trị lớn nhất, giá trị nhỏ nhất trên đoạn [-1;3]tại 2 điểm
x
1
;
x
2
. Tính giá trị của biểu thức
M
x
1
+
x
2
+
x
1
.
x
2
A. ...
Đọc tiếp
Hàm số y = x 3 3 - x 2 - x đạt giá trị lớn nhất, giá trị nhỏ nhất trên đoạn [-1;3]tại 2 điểm x 1 ; x 2 . Tính giá trị của biểu thức M = x 1 + x 2 + x 1 . x 2
A. M = 11 10
B. M = 9 10
C. M = 1
D. M = 3 4
Bài 1: Tìm giá trị nhỏ nhất của các biểu thứca ) A x2 – 2x+5b) B x2 –x +1c) C ( x -1). ( x +2). ( x+3). ( x+6)d) D x2 + 5y2 – 2xy+ 4y+3Bài 2: Tìm giá trị lớn nhất của các biểu thức sau:a) A -x2 – 4x – 2 b) B -2x2 – 3x +5c) C ( 2- x). ( x +4)d) D -8x2 + 4xy - y2 +3Bài 3 : Chứng minh rằng các giá trị của các biểu thức sau luôn dương với mọi giá trị của biếna) A 25x – 20x+7b) B 9x2 – 6xy + 2y2 +1c) E x2 – 2x + y2 + 4y+6d) D x2 – 2x +2Giúp mình nha. Cần gấp ạ Chi tiết nha
Đọc tiếp
Bài 1: Tìm giá trị nhỏ nhất của các biểu thức
a ) A= x2 – 2x+5
b) B= x2 –x +1
c) C= ( x -1). ( x +2). ( x+3). ( x+6)
d) D= x2 + 5y2 – 2xy+ 4y+3
Bài 2: Tìm giá trị lớn nhất của các biểu thức sau:
a) A= -x2 – 4x – 2
b) B= -2x2 – 3x +5
c) C= ( 2- x). ( x +4)
d) D= -8x2 + 4xy - y2 +3
Bài 3 : Chứng minh rằng các giá trị của các biểu thức sau luôn dương với mọi giá trị của biến
a) A= 25x – 20x+7
b) B= 9x2 – 6xy + 2y2 +1
c) E= x2 – 2x + y2 + 4y+6
d) D= x2 – 2x +2
Giúp mình nha. Cần gấp ạ <Chi tiết nha>
Bài 3:
a) Ta có: \(A=25x^2-20x+7\)
\(=\left(5x\right)^2-2\cdot5x\cdot2+4+3\)
\(=\left(5x-2\right)^2+3>0\forall x\)(đpcm)
d) Ta có: \(D=x^2-2x+2\)
\(=x^2-2x+1+1\)
\(=\left(x-1\right)^2+1>0\forall x\)(đpcm)
Đúng 0
Bình luận (0)
Bài 1:
a) Ta có: \(A=x^2-2x+5\)
\(=x^2-2x+1+4\)
\(=\left(x-1\right)^2+4\ge4\forall x\)
Dấu '=' xảy ra khi x=1
b) Ta có: \(B=x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
tìm giá trị nhỏ nhất của biểu thức A=(x-3)2+2
tìm giá trị nhỏ nhất của biểu thức B=11-x2
+) \(A=\left(x-3\right)^2+2\)
Vì \(\left(x-3\right)^2\)≥0 ∀x
⇒\(A\)≥2 ∀x
Min A=2⇔\(x=3\)
+) \(B=11-x^2\)
Câu này chỉ tìm được max thôi nha
Đúng 1
Bình luận (2)
\(A=\left(x-3\right)^2+2\)
Vì \(\left(x-3\right)^2\ge0\)
\(\Rightarrow\left(x-3\right)^2+2\ge2\)
Vậy GTNN của A là 2 khi x = 3
Đúng 1
Bình luận (0)
Bài 6:Tìm giá trị lớn nhất của biểu thứca) A-x2+6x-11 b) B5-8x-x2 c) C4x-x2+1Bài 7:Tìm giá trị nhỏ nhất của biểu thứca) Ax2-6x+11 b) Bx2-2x+y2+4y+8 c) Cx2-4xy+5y2+10x-22y+28
Đọc tiếp
Bài 6:Tìm giá trị lớn nhất của biểu thức
a) A=-x2+6x-11 b) B=5-8x-x2 c) C=4x-x2+1
Bài 7:Tìm giá trị nhỏ nhất của biểu thức
a) A=x2-6x+11 b) B=x2-2x+y2+4y+8 c) C=x2-4xy+5y2+10x-22y+28
Bài 6:
a) Ta có: \(A=-x^2+6x-11\)
\(=-\left(x^2-6x+11\right)\)
\(=-\left(x-3\right)^2-2\le-2\forall x\)
Dấu '=' xảy ra khi x=3
b) Ta có: \(B=-x^2-8x+5\)
\(=-\left(x^2+8x-5\right)\)
\(=-\left(x^2+8x+16-21\right)\)
\(=-\left(x+4\right)^2+21\le21\forall x\)
Dấu '=' xảy ra khi x=-4
c) Ta có: \(C=-x^2+4x+1\)
\(=-\left(x^2-4x-1\right)\)
\(=-\left(x^2-4x+4-5\right)\)
\(=-\left(x-2\right)^2+5\le5\forall x\)
Dấu '=' xảy ra khi x=2
Đúng 0
Bình luận (0)
Bài 7:
a) Ta có: \(x^2-6x+11\)
\(=x^2-6x+9+2\)
\(=\left(x-3\right)^2+2\ge2\forall x\)
Dấu '=' xảy ra khi x=3
Đúng 0
Bình luận (0)
1- Tìm x để biểu thức 3−x2+2x3−x2+2x có giá trị lớn nhất .2- Tìm x để biểu thức 3(2x+9)2−13(2x+9)2−1 có giá trị nhỏ nhất3- Tìm giá trị rút gọn của (x−1)(x+2)−(x+1)x(x−1)(x+2)−(x+1)x4- 511a11711511a11711 . Tìm số a thỏa mãn5- Giá trị nhỏ nhất của M|x+3|+|x-5|6- Giá trị lớn nhất của A|x+13|+647- Bậc của đơn thức 12x2y5z312x2y5z38- (13)2017×32016×21(13)2017×32016×219- Nghiệm của đa thức x2−60x+900x2−60x+90010- Giá trị rút gọn (2x−4)(x+3)−2x(x+1)
Đọc tiếp
1- Tìm x để biểu thức 3−x2+2x3−x2+2x có giá trị lớn nhất .
2- Tìm x để biểu thức 3(2x+9)2−13(2x+9)2−1 có giá trị nhỏ nhất
3- Tìm giá trị rút gọn của (x−1)(x+2)−(x+1)x(x−1)(x+2)−(x+1)x
4- 511<a11<711511<a11<711 . Tìm số a thỏa mãn
5- Giá trị nhỏ nhất của M=|x+3|+|x-5|
6- Giá trị lớn nhất của A=|x+13|+64
7- Bậc của đơn thức 12x2y5z312x2y5z3
8- (13)2017×32016×21(13)2017×32016×21
9- Nghiệm của đa thức x2−60x+900x2−60x+900
10- Giá trị rút gọn (2x−4)(x+3)−2x(x+1)