Ta có:
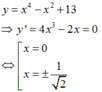
Hàm số đã cho liên tục trên - 2 ; 3 và
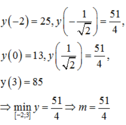
Chọn: D
Ta có:
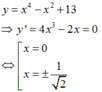
Hàm số đã cho liên tục trên - 2 ; 3 và
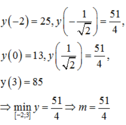
Chọn: D
Cho hàm số y = f x = log 0 , 5 x - 1 + m 2 - m (m là tham số). Biết rằng có hai giá trị ; để gía trị nhỏ nhất của hàm số trên đoạn bằng 13.
Tính T = m 1 2 - m 1 m 2 2 - m 2
A. T = 9
B. T = 36
C. T = 4
D. T = 64
Tìm m để giá trị lớn nhất của hàm số y = x 2 + 2 x + m - 4 trên đoạn - 2 ; 1 đạt giá trị nhỏ nhất. Giá trị của m là
A. 5
B. 4
C. 1
D. 3
Cho hàm số y = f ( x ) = x - m 2 x + 4 với m là số thực. Tìm giá trị lớn nhất của m để hàm số f(x) có giá trị nhỏ nhất trên [0;1] bằng -1
A. m = 2
B. m = 0
C. m 6
D. m = 3
Tổng giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f x = x - 6 x 2 + 4 trên đoạn [0;3] có dạng a - b c với a là số nguyên và b, c là các số nguyên dương. Tính S = a + b+ c
A. S = 4
B. S = -2
C. S =-22
D. S = 5
Giá trị lớn nhất của hàm số y = 2 mx + 1 m - x trên 2 ; 3 là - 1 3 khi m nhận giá trị bằng:
A. -5
B. 1
C. 0
D. -2
Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f(x) = x 2 - 16 x trên đoạn [-4;-1]. Tính T = M + m.
A. T = 32.
B. T = 16.
C. T = 37.
D. T = 25.
Gọi m 0 là giá trị nhỏ nhất của tham số thực m thỏa mãn hàm số y = x 3 3 + m x 2 + 3 m x + m nghịch biến trên một đoạn có độ dài bằng 2. Tính gần đúng P = m 0 5 + 2 m 0 + 1 3 . Kết quả làm tròn đến hàng phần trăm.
A. P ≈ 6 , 30
B. P ≈ 1 , 01
C. P ≈ 0 , 73
D. P ≈ 7 , 37
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 3 cos x - 1 3 + cos x Tổng M+m là
A. -7/3
B. 1/6
C. -5/2
D. -3/2
Cho hàm số y = f ( x ) xác định và liên tục trên ℝ , có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y = f ( x ) trên đoạn - 2 ; 2
 .
.
A. m = -5, M = 0
B. m = -5, M = -1
C. m = -1, M = 0
D. m = -2, M = 2
Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x 3 - 2 x 2 + 3 x - 4 trên đoạn [1;3] Khi đó, giá trị M-m bằng:
A. 12
B. 14
C. 2
D. 16