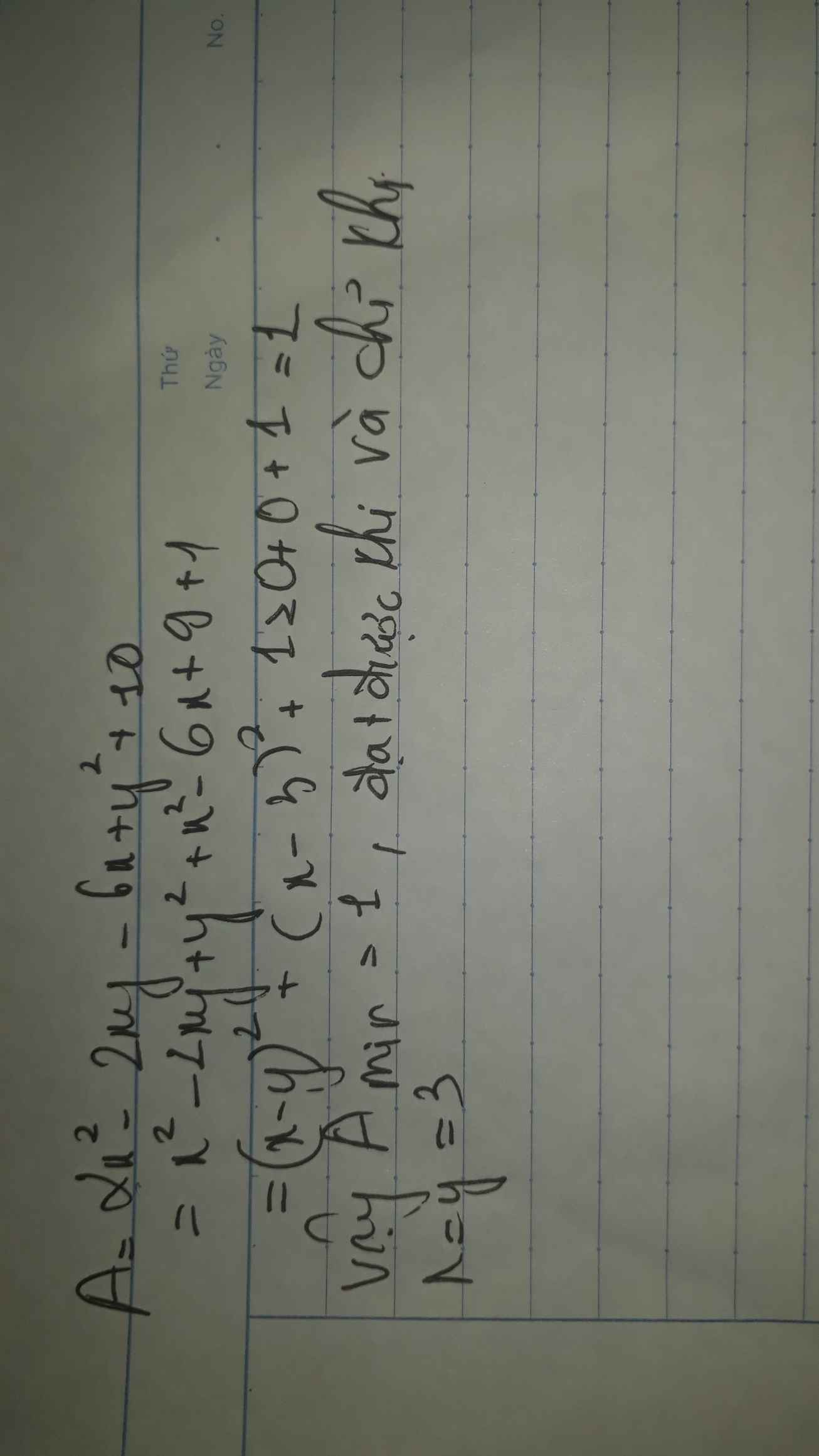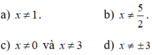`2/[6x-5-9x^2]`

`=-2/[9x^2-6x+5]`

`=-2/[(3x-1)^2+4]`

Vì `(3x-1)^2 >= 0 AA x`

`<=>(3x-1)^2+4 >= 4 AA x`

`<=>1/[(3x-1)^2+4] <= 1/4`

`<=>-2/[(3x-1)^2+4] >= -1/2 AA x`

   `=>Mi n=-1/2`

Dấu "`=`" xảy ra `<=>3x-1=0<=>x=1/3`

`A=2x^2-2xy-6x+y^2+10`

`A=x^2-2xy+y^2+x^2-6x+10`

`A=(x-y)^2+x^2-6x+9+1`

`A=(x-y)^2+(x-3)^2+1`

Vì `(x-y)^2+(x-3)^2>=0=>A>=1`

Dấu "=" xảy ra khi `{(x-y=0),(x-3=0):}<=>x=y=3`

A=\(\left(x^2-2xy+y^2\right)+\left(x^2-6x+9\right)+1=\left(x-y\right)^2+\left(x-3\right)^2+1\ge1\\ \)

dấu= xảy ra khi x=y=3

tick mik nha

Với \(x\ge\dfrac{1}{3}\Leftrightarrow B=9x^2-6x-4\left(3x-1\right)+6=9x^2-18x+10\)

\(B=9\left(x^2-2x+1\right)+1=9\left(x-1\right)^2+1\ge1\\ B_{min}=1\Leftrightarrow x=1\left(1\right)\)

Với \(x< \dfrac{1}{3}\Leftrightarrow B=9x^2-6x+4\left(3x-1\right)+6=9x^2+6x+2\)

\(B=\left(9x^2+6x+1\right)+1=\left(3x+1\right)^2+1\ge1\\ B_{min}=1\Leftrightarrow x=-\dfrac{1}{3}\left(2\right)\)

\(\left(1\right)\left(2\right)\Leftrightarrow B_{min}=1\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{3}\end{matrix}\right.\)

\(C=2x^2+4x+2+3x^2+12x+12-4x^2-24x-36\\ C=x^2-8x-22=\left(x^2-8x+16\right)-38=\left(x-4\right)^2-38\ge-38\\ C_{min}=-38\Leftrightarrow x=4\)

Với \(x\ge\dfrac{1}{6}\Leftrightarrow A=5x^2-6x+1-1=5x^2-6x\)

\(A=5\left(x^2-2\cdot\dfrac{3}{5}x+\dfrac{9}{25}\right)-\dfrac{9}{5}=5\left(x-\dfrac{3}{5}\right)^2-\dfrac{9}{5}\ge-\dfrac{9}{5}\\ A_{min}=-\dfrac{9}{5}\Leftrightarrow x=\dfrac{3}{5}\left(1\right)\)

Với \(x< \dfrac{1}{6}\Leftrightarrow A=5x^2+6x-1-1=5x^2+6x-2\)

\(A=5\left(x^2+2\cdot\dfrac{3}{5}x+\dfrac{9}{25}\right)-\dfrac{19}{5}=5\left(x+\dfrac{3}{5}\right)^2-\dfrac{19}{5}\ge-\dfrac{19}{5}\\ A_{min}=-\dfrac{19}{5}\Leftrightarrow x=-\dfrac{3}{5}\left(2\right)\\ \left(1\right)\left(2\right)\Leftrightarrow A_{min}=-\dfrac{19}{5}\Leftrightarrow x=-\dfrac{3}{5}\)

b:=y^2+2y+1+9x^2-12x+4

=(y+1)^2+(3x-2)^2

a:

SỬa đề: 5y^2

=y^2-10y+25+9x^2+4y^2-12xy

=(y-5)^2+(3x-2y)^2

`M=-9x^2+6x-3`

`M=-(9x^2-6x+3)`

`M=-(9x^2-6x+1+2)`

`M=-(3x-1)^2-2`

Vì `-(3x-1)^2 <= 0 AA x`

`<=>-(3x-1)^2-2 <= -2 AA x`

  Hay `M <= -2 AA x`

Dấu "`=`" xảy ra `<=>(3x-1)^2=0<=>3x-1=0<=>x=1/3`

Vậy `GTLN` của `M` là `-2` khi `x=1/3`

\(M=-9x^2+6x-3\)

\(M=-\left(9x^2-6x+3\right)\)

\(M=-\left[\left(3x-1\right)^2+2\right]\)

\(M=-\left(3x-1\right)^2-2\)

\(\Rightarrow Max_M=-2\) khi \(3x-1=0\)

                                 \(\Leftrightarrow x=\dfrac{1}{3}\)

`-9x^2 + 6x - 3`.

`= -(3x - 1)^2 - 2`.

Vì `(3x-1)^2 >=0 => -(3x-1)^2 <=0 => -(3x-1)^2 - 2 <= -2`

Dấu bằng xảy ra `<=> 3x - 1 = 0 => x = 1/3`.

Vậy `Max_M = -2 <=> x = 1/3`.

Áp dụng Bunyakovsky, ta có :

\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x.1+y.1\right)^2=1\)

=> \(\left(x^2+y^2\right)\ge\frac{1}{2}\)

=> \(Min_C=\frac{1}{2}\Leftrightarrow x=y=\frac{1}{2}\)

Mấy cái kia tương tự 

\(B=y^2-y+1\)

\(=y^2-2\cdot y\cdot\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2-\dfrac{1}{4}+1\)

\(=\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)

Ta thấy: \(\left(y-\dfrac{1}{2}\right)^2\ge0\forall y\)

\(\Rightarrow\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall y\)

Dấu \("="\) xảy ra \(\Leftrightarrow y-\dfrac{1}{2}=0\Leftrightarrow y=\dfrac{1}{2}\)

Vậy \(B_{min}=\dfrac{3}{4}\) khi \(y=\dfrac{1}{2}\).

\(---\)

\(C=x^2-4x+y^2-y+5\)

\(=\left(x^2-4x+4\right)+\left(y^2-y+\dfrac{1}{4}\right)+\dfrac{3}{4}\)

\(=\left(x^2-2\cdot x\cdot2+2^2\right)+\left[y^2-2\cdot y\cdot\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2\right]+\dfrac{3}{4}\)

\(=\left(x-2\right)^2+\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)

Ta thấy: \(\left(x-2\right)^2\ge0\forall x\)

              \(\left(y-\dfrac{1}{2}\right)^2\ge0\forall y\)

\(\Rightarrow\left(x-2\right)^2+\left(y-\dfrac{1}{2}\right)^2\ge0\forall x;y\)

\(\Rightarrow\left(x-2\right)^2+\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x;y\)

Dấu \("="\) xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x-2=0\\y-\dfrac{1}{2}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{1}{2}\end{matrix}\right.\)

Vậy \(C_{min}=\dfrac{3}{4}\) khi \(x=2;y=\dfrac{1}{2}\).

\(Toru\)

\(B=y^2-y+1\)

\(=y^2-2.y.\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}=\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)

Vì \(\left(y-\dfrac{1}{2}\right)^2\ge0\forall y\Rightarrow B\ge\dfrac{3}{4}\)

Dấu "=" xảy ra \(\Leftrightarrow y=\dfrac{1}{2}\)

\(C=x^2-4x+y^2-y+5\)

\(=x^2-4x+4+y^2-y+\dfrac{1}{4}+\dfrac{3}{4}\)

\(=\left(x-2\right)^2+\left(y-\dfrac{1}{2}\right)^2\)

Vì \(\left(x-2\right)^2+\left(y-\dfrac{1}{2}\right)^2\ge0\forall x,y\)

Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{1}{2}\end{matrix}\right.\)

\(P=\left(x^2-6x+9\right)+\left(y^2-2y+1\right)+2\\ P=\left(x-3\right)^2+\left(y-1\right)^2+2\ge2\\ P_{min}=2\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\)