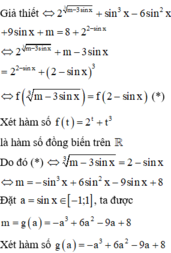\( 2)\sin x + \sin 2x + \sin 3x = 0\\ \Leftrightarrow 2\sin 2x.\cos x + \sin 2x = 0\\ \Leftrightarrow \sin 2x\left( {2\cos x + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l} \sin 2x = 0\\ 2\cos x + 1 = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} 2x = k\pi \\ \cos x = \dfrac{{ - 1}}{2} \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = \dfrac{{k\pi }}{2}\\ x = \pm \dfrac{{2\pi }}{3} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z} } \right) \)

\( 3)\sin x + \sin 2x + \sin 3x + \sin 4x = 0\\ \Leftrightarrow \left( {\sin x + \sin 4x} \right) + \left( {\sin 2x + \sin 3x} \right) = 0\\ \Leftrightarrow 2\sin \dfrac{{5x}}{2}.\cos \dfrac{{3x}}{2} + 2\sin \dfrac{{5x}}{2}.\cos \dfrac{x}{2} = 0\\ \Leftrightarrow \sin \dfrac{{5x}}{2}.\left( {\cos \dfrac{{3x}}{2} + \cos \dfrac{x}{2}} \right) = 0\\ \Leftrightarrow \sin \dfrac{{5x}}{2}.2\cos x.\cos \dfrac{x}{2} = 0\\ \Leftrightarrow \left[ \begin{array}{l} \sin \dfrac{{5x}}{2} = 0\\ 2\cos x = 0\\ \cos \dfrac{x}{2} = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = \dfrac{{2k\pi }}{5}\\ x = \dfrac{\pi }{2} + k\pi \\ x = \pi + 2k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right) \)

\(\Leftrightarrow2cos5x.cosx=2cos5x.sin2x\)

\(\Leftrightarrow\left[{}\begin{matrix}cos5x=0\\cosx=sin2x=cos\left(\frac{\pi}{2}-2x\right)\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}5x=\frac{\pi}{2}+k\pi\\x=\frac{\pi}{2}-2x+k2\pi\\x=2x-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{10}+\frac{k\pi}{5}\\x=\frac{\pi}{6}+\frac{k2\pi}{3}\\x=\frac{\pi}{2}+k2\pi\end{matrix}\right.\)

ĐKXĐ: ....

\(\Leftrightarrow\frac{cos2x}{sin3x}+\frac{cos2\left(3x\right)}{sin3\left(3x\right)}+\frac{cos2\left(9x\right)}{sin3\left(9x\right)}=0\)

Xét biểu thức \(\frac{cos2a}{sin3a}=\frac{cos2a.sina}{sin3a.sina}=\frac{sin3a-sina}{2sin3a.sina}=\frac{1}{2}\left(\frac{1}{sina}-\frac{1}{sin3a}\right)\)

Vậy pt tương đương:

\(\frac{1}{2}\left(\frac{1}{sinx}-\frac{1}{sin3x}+\frac{1}{sin3x}-\frac{1}{sin9x}+\frac{1}{sin9x}-\frac{1}{sin27x}\right)=0\)

\(\Leftrightarrow\frac{1}{sinx}=\frac{1}{sin27x}\Leftrightarrow sinx=sin27x\Leftrightarrow...\)

a/

\(\Leftrightarrow2cos6x.cos5x=cos6x\)

\(\Leftrightarrow cos6x\left(2cos5x-1\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}cos6x=0\\cos5x=\frac{1}{2}\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}6x=\frac{\pi}{2}+k2\pi\\5x=\pm\frac{\pi}{3}+k2\pi\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{12}+\frac{k\pi}{3}\\x=\pm\frac{\pi}{15}+\frac{k2\pi}{5}\end{matrix}\right.\)

b/

\(\Leftrightarrow sin2x+sin6x-\left(cos5x+cosx\right)=0\)

\(\Leftrightarrow2sin4x.cos2x-2cos3x.cos2x=0\)

\(\Leftrightarrow cos2x\left(sin4x-cos3x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\sin4x=cos3x=sin\left(\frac{\pi}{2}-3x\right)\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=\frac{\pi}{2}+k\pi\\4x=\frac{\pi}{2}-3x+k2\pi\\4x=3x-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+\frac{k\pi}{2}\\x=\frac{\pi}{14}+\frac{k2\pi}{7}\\x=-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)

c/

\(\Leftrightarrow sinx+sin3x+sin2x=cosx+cos3x+cos2x\)

\(\Leftrightarrow2sin2x.cosx+sin2x=2cos2x.cosx+cos2x\)

\(\Leftrightarrow sin2x\left(2cosx+1\right)=cos2x\left(2cosx+1\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}2cosx+1=0\\sin2x=cos2x=sin\left(\frac{\pi}{2}-2x\right)\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}cosx=-\frac{1}{2}\\2x=\frac{\pi}{2}-2x+k2\pi\\2x=2x-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=\pm\frac{2\pi}{3}+k2\pi\\x=\frac{\pi}{8}+\frac{k\pi}{2}\\\end{matrix}\right.\)

\(\Leftrightarrow cos5x=-sin3x\)

\(\Leftrightarrow cos5x=cos\left(\dfrac{\pi}{2}+3x\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}5x=\dfrac{\pi}{2}+3x+k2\pi\\5x=-\dfrac{\pi}{2}-3x+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=-\dfrac{\pi}{16}+\dfrac{k\pi}{4}\end{matrix}\right.\)

cos 6x+cos4x=sin7x-sin3x

=>2*cos5x*cosx=2*cos5x*sin2x

=>cos5x(cosx-sin2x)=0

=>cos5x=0 hoặc sin2x=sin(pi/2-x)

=>5x=pi/2+kpi hoặc 2x=pi/2-x+k2pi hoặc 2x=pi/2+x+k2pi

=>x=pi/10+kpi/5; x=pi/6+k2pi/3; x=pi/2+k2pi

a/

\(\Leftrightarrow\frac{\sqrt{3}}{2}sin3x+\frac{1}{2}cos3x=\frac{1}{2}sinx+\frac{\sqrt{3}}{2}cosx\)

\(\Leftrightarrow sin\left(3x+\frac{\pi}{6}\right)=sin\left(x+\frac{\pi}{3}\right)\)

\(\Rightarrow\left[{}\begin{matrix}3x+\frac{\pi}{6}=x+\frac{\pi}{3}+k2\pi\\3x+\frac{\pi}{6}=\pi-x-\frac{\pi}{3}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{12}+k\pi\\x=\frac{\pi}{8}+\frac{k\pi}{2}\end{matrix}\right.\)

b/

\(\Leftrightarrow2\left(\frac{1+cos2x}{2}\right)-3\sqrt{3}sin2x-4\left(\frac{1-cos2x}{2}\right)=-4\)

\(\Leftrightarrow3cos2x-3\sqrt{3}sin2x=-3\)

\(\Leftrightarrow\frac{\sqrt{3}}{2}sin2x-\frac{1}{2}cos2x=1\)

\(\Leftrightarrow sin\left(2x-\frac{\pi}{6}\right)=1\)

\(\Leftrightarrow2x-\frac{\pi}{6}=\frac{\pi}{2}+k2\pi\)

\(\Leftrightarrow x=\frac{\pi}{3}+k\pi\)

c/

Ủa đề câu này bạn ghi đúng ko? Nhìn kì kì, cos8x hay cos3x bên vế phải vậy?

d/

\(\Leftrightarrow\frac{1}{2}cos2x-\frac{\sqrt{3}}{2}sin2x=\frac{\sqrt{3}}{2}sinx+\frac{1}{2}cosx\)

\(\Leftrightarrow cos\left(2x+\frac{\pi}{3}\right)=cos\left(x-\frac{\pi}{3}\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+\frac{\pi}{3}=x-\frac{\pi}{3}+k2\pi\\2x+\frac{\pi}{3}=\frac{\pi}{3}-x+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{2\pi}{3}+k2\pi\\x=\frac{k2\pi}{3}\end{matrix}\right.\)

e/

\(\Leftrightarrow\frac{1}{2}sin8x-\frac{\sqrt{3}}{2}cos8x=\frac{\sqrt{3}}{2}sin6x+\frac{1}{2}cos6x\)

\(\Leftrightarrow sin\left(8x-\frac{\pi}{3}\right)=sin\left(6x+\frac{\pi}{6}\right)\)

\(\Rightarrow\left[{}\begin{matrix}8x-\frac{\pi}{3}=6x+\frac{\pi}{6}+k2\pi\\8x-\frac{\pi}{3}=\pi-6x-\frac{\pi}{6}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+k\pi\\x=\frac{\pi}{28}+\frac{k\pi}{7}\end{matrix}\right.\)