Cho 3 điểm \(A\left(-6;4\right),B\left(-3;1\right),C\left(2;-9\right)\)
a, Viết phương trình 3 đường thẳng chứa 3 cạnh tam giác
b, Viết phương trình 2 đường cao AH và BD của tam giác
c, Tìm tọa độ trực tâm H của tam giác
Cho đường thẳng (d) y = ax + b. Tìm các giá trị của a, b trong trường hợp sau:
(d) đi qua điểm \(A=\left(\sqrt{3}-\sqrt{2};1-\sqrt{6}\right)\) và \(B\left(\sqrt{2};2\right)\)
\(A\left(\sqrt{3}-\sqrt{2};1-\sqrt{6}\right)\in\left(d\right)\\ \Leftrightarrow\left(\sqrt{3}-\sqrt{2}\right)a+b=1-\sqrt{6}\left(1\right)B\left(\sqrt{2};2\right)\in\left(d\right)\\ \Leftrightarrow a\sqrt{2}+b=2\left(2\right)\\ \left(1\right)\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}a\sqrt{3}-a\sqrt{2}+b=1-\sqrt{6}\\a\sqrt{2}+b=2\end{matrix}\right.\)
Lấy 2 PT trừ nhau
\(\Leftrightarrow a\left(2\sqrt{2}-\sqrt{3}\right)=1+\sqrt{6}\\ \Leftrightarrow a=\dfrac{\sqrt{6}+1}{2\sqrt{2}-\sqrt{3}}=\dfrac{\left(\sqrt{6}+1\right)\left(2\sqrt{2}+\sqrt{3}\right)}{8-3}\\ \Leftrightarrow a=\dfrac{11\sqrt{2}+\sqrt{3}}{5}\\ \Leftrightarrow b=2-a\sqrt{2}=\dfrac{10-\sqrt{2}\left(11\sqrt{2}+\sqrt{3}\right)}{5}\\ \Leftrightarrow b=\dfrac{-12-\sqrt{6}}{5}\)
Bài 2. (1 điểm) Tính:
a) $\left( x-2y \right)\left( 3xy+6{{x}^{2}}+x \right) $;
b) $\left( 18{{x}^{4}}{{y}^{3}}-24{{x}^{3}}{{y}^{4}}+12{{x}^{3}}{{y}^{3}} \right) \, : \, \left( -6{{x}^{2}}{{y}^{3}} \right)$.
a) \(\left(x-2y\right)\left(3xy+6x^2+x\right)\)
\(=x\left(3xy+6x^2+x\right)-2y\left(3xy+6x^2+x\right)\)
\(=3x^2y+6x^3+x^2-6xy^2-12x^2y-2xy\)
\(=6x^3+x^2-9x^2y-6xy^2-2xy\)
b) \(\left(18x^4y^3-24x^3y^4+12x^3y^3\right):\left(-6x^2y^3\right)\)
\(=18x^4y^3:\left(-6x^2y^3\right)-24x^3y^4:\left(-6x^2y^3\right)+12x^3y^3:\left(-6x^2y^3\right)\)
\(=-3x^2+4xy-2x\)
a) (x-2y).(3xy+6x2+x)
= x.3xy+x.6x2+x.x-(-2y).3xy+(-2y).6x2+(-2y).x
= 3x2y+6x3+x2+6xy2-12yx2-2xy
= (3x2y-12yx2) -6x3+x2+6xy2-2xy
=-9x2y-6x3+x2+6xy2-2xy
b) (18x4y3-24x3y4+12x3y3):(-6x2y3)
= 18x4y3:(-6x2y3)-24x3y4:(-6x2y3)+12x3y3:(-6x2y3)
= -6x2+4xy-2x
=
a) (x-2y) . 3xy + 6x2 +x
= 3x2y - 6xy2 + 6x2 +x
b) (18x4y3 - 24x3y4 + 12x3y3 ): (-6x2y3)
= -3x2 + 4xy - 2x
=
a) Trong các điểm A\(\left(-1;\frac{1}{3}\right);B\left(-3;3\right);C\left(-6;-12\right)\) điểm nào thuộc đồ thị hàm số (2)
b) Hãy cho biết hàm số đồng biến khi nào và nghịch biến khi nào.
Bài 1. (1 điểm)
a) Cho $A=\left\{ 0; \, 1; \, 2; \, 3; \, 4\right\}$ ; $B=\left\{ 2; \, 3; \, 4; \, 5; \, 6\right\}$. Tìm $A \cap B$, $A \cup B$
b) Tìm tập xác định của hàm số $y=\sqrt{2-x}+5$.
a) \(A\cap B=\left\{2;3;4\right\}\\ A\cup B=\left\{0;1;2;3;4;5;6\right\}\)
b) Để hàm số xđ thì : \(2-x\ge0< =>-x\ge-2< =>x\le2\)
a giao b 2;3;4
a hợp b 0;1;2;3;4;5;6
2-x lớn hơn hoặc bằng 0
-x=-2
x=2
Trong mặt phẳng tọa độ Oxy, cho các vectơ \(\overrightarrow a = 3.\overrightarrow i - 2.\overrightarrow j ,\)\(\overrightarrow b = \left( {4; - 1} \right)\) và các điểm M (-3; 6), N(3; -3).
a) Tìm mối liên hệ giữa các vectơ \(\overrightarrow {MN} \) và \(2\;\overrightarrow a - \overrightarrow b \).
b) Các điểm O, M, N có thẳng hàng hay không?
c) Tìm điểm P(x; y) để OMNP là một hình bình hành.
Tham khảo:
a) Ta có: \(\overrightarrow b = \left( {4; - 1} \right)\) và \(\overrightarrow a = 3.\overrightarrow i - 2.\overrightarrow j \;\; \Rightarrow \;\overrightarrow a \;\left( {3; - 2} \right)\)
\( \Rightarrow 2\;\overrightarrow a - \overrightarrow b = \left( {2.3 - 4\;;\;2.\left( { - 2} \right) - \left( { - 1} \right)} \right) = \left( {2; - 3} \right)\)
Lại có: M (-3; 6), N(3; -3)
\( \Rightarrow \overrightarrow {MN} = \left( {3 - \left( { - 3} \right); - 3 - 6} \right) = \left( {6; - 9} \right)\)
Dễ thấy:\(\left( {6; - 9} \right) = 3.\left( {2; - 3} \right)\) \( \Rightarrow \overrightarrow {MN} = 3\left( {2\;\overrightarrow a - \overrightarrow b } \right)\)
b) Ta có: \(\overrightarrow {OM} = \left( { - 3;6} \right)\) ( do M(-3; 6)) và \(\overrightarrow {ON} = \left( {3; - 3} \right)\) (do N (3; -3)).
Hai vectơ này không cùng phương (vì \(\frac{{ - 3}}{3} \ne \frac{6}{{ - 3}}\)).
Do đó các điểm O, M, N không cùng nằm trên một đường thẳng.
Vậy chúng không thẳng hàng.
c) Các điểm O, M, N không thẳng hàng nên OMNP là một hình hành khi và chỉ khi \(\overrightarrow {OM} = \overrightarrow {PN} \).
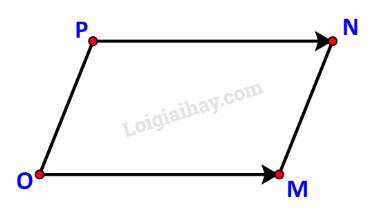
Do \(\overrightarrow {OM} = \left( { - 3;6} \right),\;\overrightarrow {PN} = \left( {3 - x; - 3 - y} \right)\) nên
\(\overrightarrow {OM} = \overrightarrow {PN} \Leftrightarrow \left\{ \begin{array}{l} - 3 = 3 - x\\6 = - 3 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 6\\y = - 9\end{array} \right.\)
Vậy điểm cần tìm là P (6; -9).
1) cho 2 đường thẳng song song a và b. Trên đường thẳng a lấy 6 điểm phân biệt. Trên đường thẳng b lấy 5 điểm phân biệt. Tính số tam giác có đỉnh là 3 trong các điểm đã cho
2)tìm a;b sao cho a+b=a:b \(\left(b\ne0\right)\)
b)cho x;y;z là 3 số nguyên dương nguyên tố cùng nhau thỏa mãn
\(\left(x-z\right)\left(y-z\right)=z^2\)
chứng minh rằng x;y;z là số chính phương
Trên đường tròn lượng giác góc A lấy điểm M sao cho số đo lượng giác \(\stackrel\frown{AM}\)=\(\alpha\) . Có bao nhiêu điểm M biết \(\alpha=\dfrac{\pi}{6}+\dfrac{k\pi}{3}\left(k\in Z\right)?\)
Cho hàm số: \(y=f\left(x\right)=\frac{6}{x}\)
a) Tính \(f\left(1\right);f\left(1,5\right);f\left(2\right);f\left(\frac{-2}{3}\right)\)
b) Tìm x khi y = 3; y = (-2)
c) Điểm nào trong các điểm sau thuộc đồ thị hàm số:
\(A\left(-1;-6\right)\) ; \(B\left(\frac{1}{2};10\right)\)
\(C\left(-\frac{1}{2};-12\right)\); \(D\left(-\frac{1}{3};-3\right)\)
Trong các điểm \(A\left(6;-2\right),B\left(-2;-10\right),C\left(1;1\right),D\left(-\dfrac{1}{3};1\dfrac{2}{3}\right),E\left(0;0\right)\) có những điểm nào thuộc đồ thị của hàm số :
a) \(y=-\dfrac{1}{3}x\)
b) \(y=5x\)
câu a gồm : A(6: -2) , E( 0; 0)
câu b gồm : B( -2; -10 ) ,E ( 0: 0)
Trong không gian Oxyz, cho bốn điểm \(A\left(6;-2;3\right),B\left(0;1;6\right),C\left(2;0;-1\right),D\left(4;1;0\right)\). Gọi (S) là mặt cầu đi qua 4 điểm A, B, C, D. Hãy viết phương trình mặt phẳng tiếp xúc với mặt cầu (S) tại điểm A ?