Tìm tất cả các giá trị của tham số m để pt có nghiệm :
a. sinx - cosx = m
b. sinx - (2m-1)cosx = m+2
Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm 2 m ( c o s x + s i n x ) = 2 m 2 + c o s x - sin x + 3 2
A. - 1 2 > m < 1 2
B. m = ± 1 2
C. - 1 4 > m < 1 4
D. m = ± 1 4
1, cho phương trình \(sin2x-\left(2m+\sqrt{2}\right)\left(sinx+cosx\right)+2m\sqrt{2}+1=0\) tìm các giá trị m để phương trình có đúng 2 nghiệm \(x\in\left(0;\dfrac{5\Pi}{4}\right)\)
2,tìm tất cả các giá trị thực của tham số m để phương trình \(cos2x+\left(2m+1\right)sinx-m-1=0\) có đúng 2 nghiệm thuộc khoảng \(\left(\dfrac{\Pi}{2};\dfrac{3\Pi}{2}\right)\)
3, cho phương trình \(cos^2x-2mcosx+6m-9=0\) tìm các giá trị m để phương trình có nghiệm thuộc khoảng \(\left(-\dfrac{\Pi}{2};\dfrac{\Pi}{2}\right)\)
Số giá trị nguyên của tham số m để phương trình sin x + ( m − 1 ) cos x = 2 m − 1 có nghiệm là
A. 0
B. 3
C. 2
D. 1
Số giá trị nguyên của tham số m để phương trình sin x + ( m - 1 ) cos x = 2 m - 1 có nghiệm là
A. 0
B. 3
C. 2
D. 1
tìm tất cả các giá trị của m để phương trình \(\dfrac{sinx+2}{cosx}=m\) vô nghiệm
\(\Rightarrow sinx+2=m.cosx\)
\(\Rightarrow sinx-m.cosx=-2\)
Pt đã cho vô nghiệm khi:
\(1^2+\left(-m\right)^2< \left(-2\right)^2\)
\(\Rightarrow m^2< 3\)
\(\Rightarrow-\sqrt{3}< m< \sqrt{3}\)
Tìm tất cả giá trị của m để phương trình sin2x – 2( m- 1)sinx. cosx – (m- 1).cos2x = m có nghiệm?
A. 0 ≤ m ≤ 1
B.m> 1
C.0< m< 1
D. m ≤ 0
Hướng dẫn giải:
Chọn A.
Ta có: sin2x – 2( m- 1)sinx. cosx – (m- 1).cos2x = m
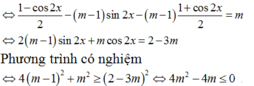
![]()
Bài 1: Tìm m để các phương trình sau có nghiệm
a) \((m+2)sinx+mcosx=2\)
b) \(msinx+(m-1)cosx=2m+1\)
c) \((m+2)sin2x+mcos^2x=m-2+msin^2x\)
Bài 2: Tìm m để các phương trình sau vô nghiệm
a) \((2m-1)sinx+(m-1)cosx=m-3\)
b) \(2sinx+cosx=m(sinx-2cosx+3)\)
1.
a, Phương trình có nghiệm khi:
\(\left(m+2\right)^2+m^2\ge4\)
\(\Leftrightarrow m^2+4m+4+m^2\ge4\)
\(\Leftrightarrow2m^2+4m\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}m\ge0\\m\le-2\end{matrix}\right.\)
b, Phương trình có nghiệm khi:
\(m^2+\left(m-1\right)^2\ge\left(2m+1\right)^2\)
\(\Leftrightarrow2m^2+6m\le0\)
\(\Leftrightarrow-3\le m\le0\)
2.
a, Phương trình vô nghiệm khi:
\(\left(2m-1\right)^2+\left(m-1\right)^2< \left(m-3\right)^2\)
\(\Leftrightarrow4m^2-4m+1+m^2-2m+1< m^2-6m+9\)
\(\Leftrightarrow4m^2-7< 0\)
\(\Leftrightarrow-\dfrac{\sqrt{7}}{2}< m< \dfrac{\sqrt{7}}{2}\)
b, \(2sinx+cosx=m\left(sinx-2cosx+3\right)\)
\(\Leftrightarrow\left(m-2\right)sinx-\left(2m+1\right)cosx=-3m\)
Phương trình vô nghiệm khi:
\(\left(m-2\right)^2+\left(2m+1\right)^2< 9m^2\)
\(\Leftrightarrow m^2-4m+4+4m^2+4m+1< 9m^2\)
\(\Leftrightarrow m^2-1>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\)
1.
c, \(\left(m+2\right)sin2x+mcos^2x=m-2+msin^2x\)
\(\Leftrightarrow\left(m+2\right)sin2x+m\left(cos^2x-sin^2x\right)=m-2\)
\(\Leftrightarrow\left(m+2\right)sin2x+mcos2x=m-2\)
Phương trình vô nghiệm khi:
\(\left(m+2\right)^2+m^2< \left(m-2\right)^2\)
\(\Leftrightarrow m^2+4m+4+m^2< m^2-4m+4\)
\(\Leftrightarrow m^2+8m< 0\)
\(\Leftrightarrow-8\le m\le0\)
Gọi \(S\) là tập hợp các giá trị nguyên của tham số \(m\) để phương trình \(\sqrt{2019}sinx-cosx=2m\) có nghiệm. Tổng tất các các phẩn tử của S bằng
A. -1
B. 2
C. 1
D. 0
Để phương trình có nghiệm thì \(\left(\sqrt{2019}\right)^2+\left(-1\right)^2>=4m^2\)
=>4m^2<=2020
=>m^2<=505
mà m nguyên
nên \(m^2\in\left\{0;1;...;22^2\right\}\)
=>\(m\in\left\{-22;-21;...;21;22\right\}\)
=>Tổng các phần tử là 0
=>Chọn D
số các giá trị nguyên của tham số m thuộc ( -2020;2020) để phương trình : ( m+1)cosx+(m-1)sinx =2m+3 có 2 nghiệm x1,x2 thỏa mãn \(\left|x_1-x_2\right|=\dfrac{\pi}{3}\) là