a: \(\overrightarrow{BA}-\overrightarrow{BC}=\overrightarrow{BA}+\overrightarrow{CB}=\overrightarrow{CA}\)

b: lấy điểm H sao cho \(\overrightarrow{AH}=\overrightarrow{GC}\)

\(\overrightarrow{AH}=\overrightarrow{GC}\)

=>AH//GC và AH=GC

Xét tứ giác AHCG có

AH//CG

AH=GC

Do đó: AHCG là hình bình hành

ΔABC đều có G là trọng tâm

nên \(AG=GB=GC=\dfrac{a\sqrt{3}}{3}\)

\(\left|\overrightarrow{AB}-\overrightarrow{GC}\right|=\left|\overrightarrow{AB}-\overrightarrow{AH}\right|\)

\(=\left|\overrightarrow{HA}+\overrightarrow{AB}\right|=\left|\overrightarrow{HB}\right|=HB\)

AHCG là hình bình hành

=>HC=AG và HC//AG

=>\(HC=\dfrac{a\sqrt{3}}{3}\)

ΔABC đều có G là trọng tâm

nên GB=GC=GA

GB=GC

AB=AC

Do đó: AG là đường trung trực của BC

=>AG\(\perp\)BC

mà CH//AG

nên CH\(\perp\)CB

=>ΔCHB vuông tại C

=>\(BH^2=HC^2+BC^2\)

=>\(BH^2=\left(\dfrac{a\sqrt{3}}{3}\right)^2+a^2=a^2+\dfrac{1}{3}a^2=\dfrac{4}{3}a^2\)

=>\(BH=a\cdot\dfrac{2\sqrt{3}}{3}\)

=>\(\left|\overrightarrow{AB}-\overrightarrow{GC}\right|=BH=\dfrac{2a\sqrt{3}}{3}\)

a. \(=\widehat{ABC}=60^o\)

b. \(=120^o\)

c. \(=30^o\)

\(T=\overrightarrow{GA}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)+\overrightarrow{GB}.\overrightarrow{CA}+\overrightarrow{GC}.\overrightarrow{AB}\)

\(=\overrightarrow{AB}\left(\overrightarrow{GC}-\overrightarrow{GA}\right)+\overrightarrow{AC}\left(\overrightarrow{GA}-\overrightarrow{GB}\right)\)

\(=\overrightarrow{AB}\left(\overrightarrow{GC}+\overrightarrow{AG}\right)+\overrightarrow{AC}\left(\overrightarrow{GA}+\overrightarrow{BG}\right)\)

\(=\overrightarrow{AB}.\overrightarrow{AC}+\overrightarrow{AC}.\overrightarrow{BA}\)

\(=0\)

Cách 1:

Gọi O là giao điểm của AC và BD.

Ta có:

\(\begin{array}{l}\overrightarrow {AG}  = \overrightarrow {AB}  + \overrightarrow {BG}  = \overrightarrow a  + \overrightarrow {BG} ;\\\overrightarrow {CG}  = \overrightarrow {CB}  + \overrightarrow {BG}  = \overrightarrow {DA}  + \overrightarrow {BG}  = - \overrightarrow b  + \overrightarrow {BG} ;\end{array}\)(*)

Lại có: \(\overrightarrow {BD} =\overrightarrow {BA}  + \overrightarrow {AD} =  - \overrightarrow a  + \overrightarrow b \).

\(\overrightarrow {BG} ,\overrightarrow {BD} \) cùng phương và \(\left| {\overrightarrow {BG} } \right| = \frac{2}{3}BO = \frac{1}{3}\left| {\overrightarrow {BD} } \right|\)

\( \Rightarrow \overrightarrow {BG}  = \frac{1}{3}\overrightarrow {BD}  = \frac{1}{3}\left( { - \overrightarrow a  + \overrightarrow b } \right)\)

Do đó (*) \( \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {AG}  = \overrightarrow a  + \overrightarrow {BG}  = \overrightarrow a  + \frac{1}{3}\left( { - \overrightarrow a  + \overrightarrow b } \right) = \frac{2}{3}\overrightarrow a  + \frac{1}{3}\overrightarrow b ;\\\overrightarrow {CG}  = -\overrightarrow b  + \overrightarrow {BG}  = -\overrightarrow b  + \frac{1}{3}\left( { - \overrightarrow a  + \overrightarrow b } \right) =  - \frac{1}{3}\overrightarrow a  - \frac{2}{3}\overrightarrow b ;\end{array} \right.\)

Vậy \(\overrightarrow {AG}  = \frac{2}{3}\overrightarrow a  + \frac{1}{3}\overrightarrow b ;\;\overrightarrow {CG}  =  - \frac{1}{3}\overrightarrow a  - \frac{2}{3}\overrightarrow b .\)

Cách 2:

Gọi AE, CF là các trung tuyến trong tam giác ABC.

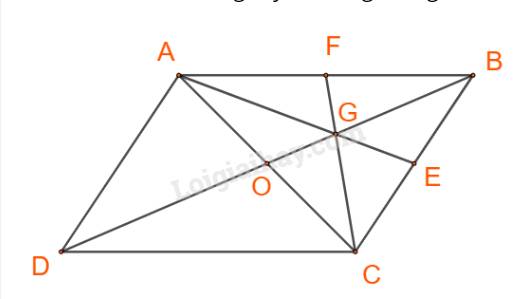
Ta có: 

\(\overrightarrow {AG}  = \frac{2}{3}\overrightarrow {AE}  = \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right) = \frac{2}{3}.\frac{1}{2}\left[ {\overrightarrow {AB}  + \left( {\overrightarrow {AB}  + \overrightarrow {AD} } \right)} \right] \\= \frac{1}{3}\left( {2\overrightarrow a  + \overrightarrow b } \right) = \frac{2}{3}\overrightarrow a  + \frac{1}{3}\overrightarrow b \)

\(\overrightarrow {CG}  = \frac{2}{3}\overrightarrow {CF}  = \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {CA}  + \overrightarrow {CB} } \right) = \frac{2}{3}.\frac{1}{2}\left[ {\left( {\overrightarrow {CB}  + \overrightarrow {CD} } \right) + \overrightarrow {CB} } \right] = \frac{1}{3}\left( {2\overrightarrow {CB}  + \overrightarrow {CD} } \right) = \frac{1}{3}\left( { - 2\overrightarrow {AD}  - \overrightarrow {AB} } \right) =  - \frac{1}{3}\overrightarrow a  - \frac{2}{3}\overrightarrow b \)

Vậy \(\overrightarrow {AG}  = \frac{2}{3}\overrightarrow a  + \frac{1}{3}\overrightarrow b ;\;\overrightarrow {CG}  =  - \frac{1}{3}\overrightarrow a  - \frac{2}{3}\overrightarrow b .\)

Bài 3: 

Tham khảo: