x6 - x3 + x2 - x + 1
Tìm nghiệm của đa thức trên

Những câu hỏi liên quan
Bài 1: tìm x biết:
a)(x-8 ).( x3+8)=0
b)( 4x-3)-( x+5)=3.(10-x )
bài 2: cho hai đa thức sau:
f( x)=( x-1).(x+2 )
g(x)=x3+ax2+bx+2
Xác định a và b biết nghiệm của đa thức f(x)cũng là nghiệm của đa thức g(x)
Bài 1.
a.\(\left(x-8\right)\left(x^3+8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-8=0\\x^3+8=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)
b.\(\left(4x-3\right)-\left(x+5\right)=3\left(10-x\right)\)
\(\Leftrightarrow4x-3-x-5=30-3x\)
\(\Leftrightarrow4x-x+3x=30+5+3\)
\(\Leftrightarrow6x=38\)
\(\Leftrightarrow x=\dfrac{19}{3}\)
Đúng 2
Bình luận (0)
Bài 1:
a. $(x-8)(x^3+8)=0$
$\Rightarrow x-8=0$ hoặc $x^3+8=0$
$\Rightarrow x=8$ hoặc $x^3=-8=(-2)^3$
$\Rightarrow x=8$ hoặc $x=-2$
b.
$(4x-3)-(x+5)=3(10-x)$
$4x-3-x-5=30-3x$
$3x-8=30-3x$
$6x=38$
$x=\frac{19}{3}$
Đúng 3
Bình luận (0)
Bài 2:
$f(x)=(x-1)(x+2)=0$
$\Leftrightarrow x-1=0$ hoặc $x+2=0$
$\Leftrightarrow x=1$ hoặc $x=-2$
Vậy $g(x)$ cũng có nghiệm $x=1$ và $x=-2$
Tức là:
$g(1)=g(-2)=0$
$\Rightarrow 1+a+b+2=-8+4a-2b+2=0$
$\Rightarrow a=0; b=-3$
Đúng 4
Bình luận (0)
Xem thêm câu trả lời
cho đa thức A(x)=-x2+3x-2
a)chứng minh đa thức trên vô nghiệm
b)tìm gtln của A(x)
cho đa thức:
P(x)- 5x3+2x4-x2+3x2-x3-2x4+1-4x3
a, Thu gọn vắp sếp các hạng tuwrcuar đa thức trên theo lỹ thừa giảm của biến
b,Tính P(1) và P(-1)
c,Chứng tỏ rằng đa thức trên không có nghiệm
a: \(P\left(x\right)=\left(2x^4-2x^4\right)+\left(5x^3-x^3-4x^3\right)-x^2+3x^2+1=2x^2+1\)
b: P(1)=P(-1)=2+1=3
c: Vì \(2x^2+1>0\forall x\)
nên P(x) ko có nghiệm
Đúng 0
Bình luận (0)
Cho hai đa thứ sau:
f(x)= (x-1)(x+2)
g(x)=x3+ax3+bx+2
Xách định a và b biết nghiệm của đa thức f(x) cũng là nghiệm của đa thức g(x)
Đặt f(x)=0
=>(x-1)(x+2)=0
=>x=1 hoặc x=-2
Vì nghiệm của f(x) cũng là nghiệm của g(x) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}1^3+a\cdot1^3+b\cdot1+2=0\\\left(-2\right)^3+a\cdot\left(-2\right)^3+b\cdot\left(-2\right)+2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=-3\\-8a-2b=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a+2b=-6\\-8a-2b=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=0\\b=-3\end{matrix}\right.\)
Đúng 0
Bình luận (0)
cho hai đa thức
a,P(x)=2x3-3x+7-x và Q(x)=-5x3+2x-3+2x-x2-2a,Thu gọn hai đa thức P(x) và Q(x).Tìm đa thức M(x)=P(x)+Q(x) và N(x)=P(x)-Q(x)
b,tìm nghiệm của đa thức M(x)
\(a,P\left(x\right)=2x^3-3x+7-x=2x^3-4x+7\\ Q\left(x\right)=-5x^3+2x-3+2x-x^2-2=-5x^3-x^2+4x-5\)
\(M\left(x\right)=2x^3-4x+7+\left(-5x\right)^3-x^2+4x-5=-3x^3-x^2+2\)
\(N\left(x\right)=2x^3-4x+7-\left(-5x\right)^3+x^2-4x+5=7x^3+x^2-8x+12\)
b,\(M\left(x\right)=-3x^3-x^2+2=0\)
Nghiệm xấu lắm bạn
Đúng 1
Bình luận (0)
H(x) = 2x^3 + 5x + 15. tìm nghiệm của đa thức trên
a(x)=x^3+5x^2-5x-2x^2+10x-18 b(x)=-x^3-5x^2+3x+2x^2-x-2 a)thu gọn và sắp xếp các đa thức trên theo lũy thừa giảm dần của biến b)tìm đa thức m(x) sao cho m(x)-A(x)=B(x) c)tìm nghiệm của đa thức m(x)
a: a(x)=x^3+3x^2+5x-18
b(x)=-x^3-3x^2+2x-2
b: m(x)=a(x)+b(x)
=x^3+3x^2+5x-18-x^3-3x^2+2x-2
=7x-20
c: m(x)=0
=>7x-20=0
=>x=20/7
Đúng 0
Bình luận (0)
tìm m để x=2 là nghiệm của đa thức x mũ 2-2mx+1
\(x=2\) là nghiệm của đa thức đã cho nên:
\(2^2-2m.2+1=0\)
\(\Leftrightarrow4m=5\Rightarrow m=\dfrac{5}{4}\)
Đúng 2
Bình luận (0)
Thay x=2 vào phương trình \(x^2-2mx+1=0\), ta được:
\(2^2-2m\cdot2+1=0\)
\(\Leftrightarrow-4m+5=0\)
\(\Leftrightarrow-4m=-5\)
hay \(m=\dfrac{5}{4}\)
Vậy: Để x=2 là nghiệm của đa thức \(x^2-2mx+1\) thì \(m=\dfrac{5}{4}\)
Đúng 2
Bình luận (0)
Cho f(x) x5 + 3x2 − 5x3 − x7 + x3 + 2x2 + x5 − 4x2 + x7; g(x) x4 + 4x3 − 5x8 − x7 + x3 + x2 − 2x7 + x4 – 4x2 − x8. Thu gọn và sắp xếp các đa thức f(x) và g(x) theo luỹ thừa giảm của biến rồi tìm bậc của đa thức đó.
Đọc tiếp
Cho f(x)= x5 + 3x2 − 5x3 − x7 + x3 + 2x2 + x5 − 4x2 + x7; g(x) = x4 + 4x3 − 5x8 − x7 + x3 + x2 − 2x7 + x4 – 4x2 − x8. Thu gọn và sắp xếp các đa thức f(x) và g(x) theo luỹ thừa giảm của biến rồi tìm bậc của đa thức đó.
f(x) = x5 + 3x2 − 5x3 − x7 + x3 + 2x2 + x5 − 4x2 + x7
= (x5 + x5) + (3x2 + 2x2 – 4x2) + (-5x3 + x3) + (-x7 + x7)
= 2x5 + x2 – 4x3.
= 2x5 - 4x3 + x2
Đa thức có bậc là 5
g(x) = x4 + 4x3 – 5x8 – x7 + x3 + x2 – 2x7 + x4 – 4x2 – x8
= (x4 + x4) + (4x3 + x3) – (5x8 + x8) – (x7 + 2x7) + (x2 – 4x2)
= 2x4 + 5x3 – 6x8 – 3x7 – 3x2
= -6x8 - 3x7 + 2x4 + 5x3 - 3x2.
Đa thức có bậc là 8.
Đúng 0
Bình luận (0)
Đa thức có bậc là 5 nhe
Tìm nghiệm của đa thức sau:
M(x)=(6+4x)(-x+2)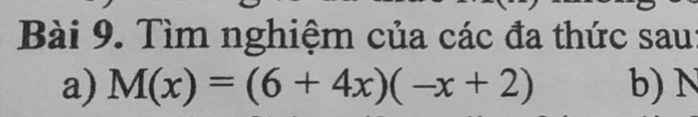
Lời giải:
$M(x)=(6+4x)(-x+2)=0$
\(\Leftrightarrow \left[\begin{matrix} 6+4x=0\\ -x+2=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=-\frac{3}{2}\\ x=2\end{matrix}\right.\)
Vậy nghiệm của đa thức $M(x)$ là $x=\frac{-3}{2}$ và $x=2$
Đúng 0
Bình luận (0)



















