tu ve hinh nha 

CÓ AB//CD

=> GÓC OAB = GOC ODC( 2 GÓC ĐỒNG VỊ )

VA  GÓC OBS = GÓC OCD ( 2 GÓC ĐỒNG VỊ )

MÀ GÓC ODC = GÓC OCD( ABCD LÀ  HÌNH THANG CÂN )

=> GÓC OAB = GÓC OBÂ

=> TAM GIAC OAB LA TAM GIÁC CÂN 

B) XÉT TAM GIÁC  BAD VÀ TAM GIÁC ABC CÓ :

AD=BC( ABCD LÀ HÌNH THANG CÂN )

AB CHUNG

AC=DC ( ABCD LA HINH THANG CÂN ) 

=>  Tam giác ABD = tgiac BAC 

C) CÓ TAM GIÁC ABC= TAM GIÁC BAD( CM CÂU B)

=> GÓC BAC = GÓC ABD ( 2 GÓC TƯƠNG ỨNG )

=> TAM GIÁC EAB CÂN TẠI E( CMT CÂU C)

=> AE=BE( ĐN TAM GIÁC CÂN )

CÓ AC = BD( ABCD LÀ HÌNH THANG CÂN )

MÀ AE = BE ( CMT)

=> ED=EC

D) CÓ AO =BO( TAM GIÁC AOB CÂN TẠI O) 

=> O THUỘC VÀO ĐƯỜNG TRUNG TRỰC CỦA AB 

CÓ EB=EB 

=> E THUỘC VÀO ĐƯỜNG TRUNG TRỰC CỦA AB 

=> OE THUỘC VÀO ĐG TT CỦA AB 

CÓ OD=OC ( CÁI NÀY TỰ CM ) 

=> O THUỘC VÀO ĐG TT CỦA CD 

CÓ ED=EC 

=> E THUỘC VÀO ĐG TT CỦA CD 

=> OE THUỘC ....... CD 

1:

a: Xét ΔOAB và ΔOCD có

\(\widehat{OAB}=\widehat{OCD}\)(hai góc so le trong, AB//CD)

AB=CD

\(\widehat{OBA}=\widehat{ODC}\)(hai góc so le trong, AB//CD)

Do đó: ΔOAB=ΔOCD

=>OA=OC và OB=OD

=>O là trung điểm chung của AC và BD

b: Xét ΔOAD và ΔOCB có

OA=OC

\(\widehat{AOD}=\widehat{COB}\)

OD=OB

Do đó: ΔOAD=ΔOCB

=>\(\widehat{OAD}=\widehat{OCB}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AD//BC

c: ΔOAD=ΔOCB

=>AD=BC

2:

a: Xét ΔAHO vuông tại H và ΔCKO vuông tại K có

OA=OC

\(\widehat{AOH}=\widehat{COK}\)

Do đó: ΔAHO=ΔCKO

=>AH=CK và OH=OK

b: Xét ΔAOK và ΔCOH có

OA=OC

\(\widehat{AOK}=\widehat{COH}\)

OK=OH

Do đó; ΔAOK=ΔCOH

=>\(\widehat{OAK}=\widehat{OCH}\)

mà hai góc này là hai góc ở vị trí so le trong

nên AK//CH

c: OH=OK

H,O,K thẳng hàng

Do đó: O là trung điểm của HK

d: AH\(\perp\)BD

CK\(\perp\)BD

Do đó: AH//CK

=>AE//CF

Xét tứ giác AECF có

AE//CF

AF//CE

Do đó: AECF là hình bình hành

=>AC cắt EF tại trung điểm của mỗi đường

mà O là trung điểm của AC

nen O là trung điểm của EF

3: Xét tứ giác AMCN có

AM//CN

AM=CN

Do đó: AMCN là hình bình hành

=>AC cắt MN tại trung điểm của mỗi đường

mà O là trung điểm của AC

nên O là trung điểm của MN

4: Xét ΔOIB và ΔOVD có

\(\widehat{IBO}=\widehat{VDO}\)

OB=OD

\(\widehat{IOB}=\widehat{VOD}\)

Do đó: ΔOIB=ΔOVD

=>BI=DV

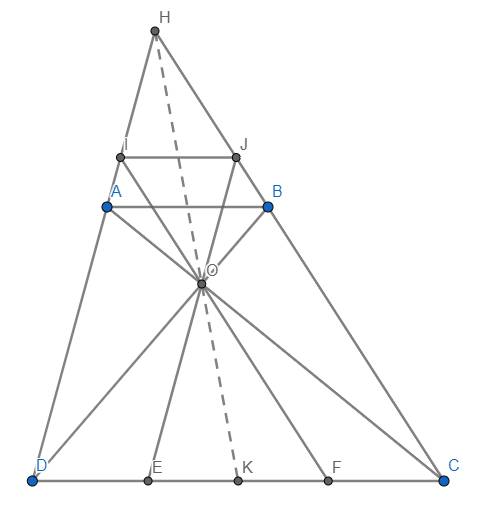
b) Theo Thales: \(\dfrac{DE}{DC}=\dfrac{AO}{AC};\dfrac{CF}{CD}=\dfrac{BO}{BD}\)

Theo câu a thì \(\dfrac{AO}{AC}=\dfrac{BO}{BD}\) \(\Rightarrow\dfrac{DE}{DC}=\dfrac{CF}{CD}\Rightarrow DE=CF\) (đpcm)

c) Từ \(DE=CF\Rightarrow\dfrac{DE}{EF}=\dfrac{CF}{EF}\)

Mà theo Thales: \(\dfrac{DE}{EF}=\dfrac{IO}{OF};\dfrac{CF}{EF}=\dfrac{JO}{OE}\) 

Do đó \(\dfrac{IO}{OF}=\dfrac{JO}{OE}\) \(\Rightarrow\) IJ//CD//AB

d) Dùng định lý Menelaus đảo nhé bạn. Ta có \(\dfrac{HA}{HD}=\dfrac{AB}{CD}=\dfrac{OA}{OC}\) nê \(\dfrac{HA}{AD}.\dfrac{OC}{OA}=1\). Do K là trung điểm EF mà \(DE=CF\) nên K cũng là trung điểm CD hay \(\dfrac{KD}{KC}=1\). Do đó \(\dfrac{HA}{AD}.\dfrac{KD}{KC}.\dfrac{OC}{OA}=1\). Theo định lý Menalaus đảo \(\Rightarrow\)H, O, K thẳng hàng (đpcm)