a: cos B=3/5 nên sin B=4/5

=>AC/BC=4/5

=>AC=8cm

=>AB=6cm

\(HC=\dfrac{8^2}{10}=6.4\left(cm\right)\)

\(M=\left(2\cdot\dfrac{3}{5}-3\cdot\dfrac{4}{5}\right):\left(1+\dfrac{4}{5}:\dfrac{3}{5}\right)\)

\(=\dfrac{-6}{5}:\left(1+\dfrac{4}{3}\right)=\dfrac{-6}{5}:\dfrac{7}{3}=\dfrac{-6}{5}\cdot\dfrac{3}{7}=\dfrac{-18}{35}\)

b: \(AD=\dfrac{AC^2}{AH}=\dfrac{8^2}{4.8}=\dfrac{40}{3}\left(cm\right)\)

\(CD=\sqrt{\left(\dfrac{40}{3}\right)^2-8^2}=\dfrac{32}{3}\left(cm\right)\)

c: \(AE\cdot EB+AF\cdot FC\)

=HE^2+HF^2

=EF^2

=AH^2

a: Xét ΔAHB vuông tại H có HE là đường cao

nên \(AE\cdot AB=AH^2\left(1\right)\)

Xét ΔAHC vuông tại H có HD là đường cao

nên \(AD\cdot AC=AH^2\left(2\right)\)

Từ (1) và (2) suy ra \(AE\cdot AB=AD\cdot AC\)

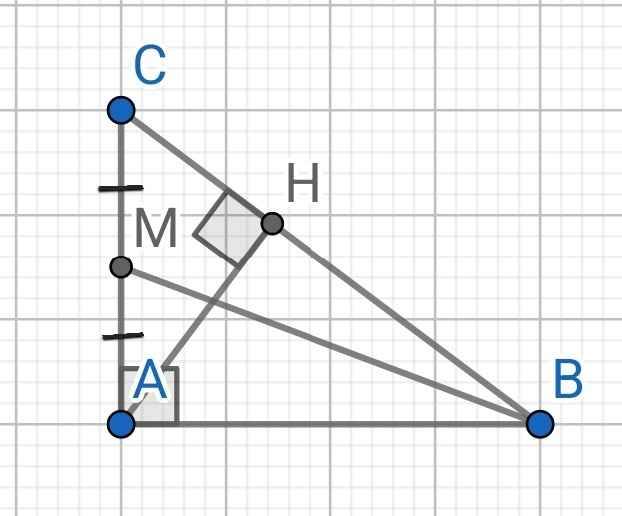
\(tanB=\dfrac{AC}{AB}=\dfrac{5}{12}\)

⇒ AC = \(\dfrac{5}{12}\) .AB

= \(\dfrac{5}{12}.5\)

\(=\dfrac{25}{12}\) (cm)

∆ABC vuông tại A

⇒ BC² = AB² + AC² (Pytago)

\(=5^2+\left(\dfrac{25}{12}\right)^2\)

= \(\dfrac{4225}{144}\)

⇒ BC = \(\dfrac{65}{12}\) (cm)

AH.BC = AB.AC

⇒ AH = AB . AC : BC

= 5 . \(\dfrac{25}{12}:\dfrac{65}{12}\)

\(=\dfrac{25}{13}\left(cm\right)\)

M là trung điểm của AC

⇒ AM = AC : 2 = \(\dfrac{25}{12}:2\) \(=\dfrac{25}{24}\) (cm)

∆ABM vuông tại A

⇒ BM² = AB² + AM²

= \(5^2+\left(\dfrac{25}{24}\right)^2\)

= \(\dfrac{15025}{576}\)

⇒ BM = \(\dfrac{5\sqrt{601}}{24}\) (cm)

Xét △ABC vuông tại A có:

\(\tan\widehat{B}=\dfrac{AC}{AB}=\dfrac{3}{4}\Rightarrow AC=\dfrac{3}{4}AB\)

Lại có: \(AB^2+AC^2=BC^2=10^2=100\)

\(\Rightarrow AB^2+\left(\dfrac{3}{4}AB\right)^2=100\)

\(\Rightarrow\dfrac{25}{16}AB^2=100\Rightarrow AB^2=64\Rightarrow AB=8\left(cm\right)\)

\(\Rightarrow AC=\dfrac{3}{4}AB=\dfrac{3}{4}.8=6\left(cm\right)\)

\(P_{ABC}=AB+BC+CA=6+10+8=24\left(cm\right)\)

Áp dụng tỉ số tanB trong tam giác vuông HAB và các hệ thức lượng trong tam giác vuông, chúng ta tính được AC = 30 13 cm; BM = 601 4 cm

Bài 1:

              \(BC=CD+BD=68+51=119\)

\(AD\)là phân giác  \(\widehat{BAC}\)\(\Rightarrow\)\(\frac{BD}{AB}=\frac{DC}{AC}\)hay     \(\frac{51}{AB}=\frac{68}{AC}\)

\(\Leftrightarrow\)\(\frac{51^2}{AB^2}=\frac{68^2}{AC^2}=\frac{51^2+68^2}{AB^2+AC^2}=\frac{25}{49}\)

suy ra:    \(\frac{51^2}{AB^2}=\frac{25}{49}\)\(\Rightarrow\)\(AB=71,4\)

ÁP dụng hệ thức lượng ta có:

           \(AB^2=BH.BC\)

\(\Leftrightarrow\)\(BH=\frac{AB^2}{BC}=\frac{71,4^2}{119}=42,84\)

\(\Rightarrow\)\(CH=BC-BH=119-42,84=76,16\)

Bài 2:

Áp dụng Pytago ta có:

     \(AH^2+BH^2=AB^2\)

\(\Leftrightarrow\)\(BH^2=AB^2-AH^2\)

\(\Leftrightarrow\)\(BH^2=7,5^2-6^2=20,25\)

\(\Leftrightarrow\)\(BH=4,5\)

Áp dụng hệ thức lượng ta có:

       \(AB^2=BH.BC\)

\(\Rightarrow\)\(BC=\frac{AB^2}{BH}=\frac{7,5^2}{4,5}=12,5\)

       \(AB.AC=BC.AH\)

\(\Rightarrow\)\(AC=\frac{BC.AH}{AB}=\frac{12,5.6}{7,5}=10\)

b)   \(cosB=\frac{AC}{BC}=\frac{10}{12,5}=0.8\)

      \(cosC=\frac{AB}{BC}=\frac{7,5}{12,5}=0,6\)

b: Xét ΔAHB vuông tại H có HM là đường cao ứng với cạnh huyền AB

nên \(AM\cdot AB=AH^2\left(1\right)\)

Xét ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC

nên \(AN\cdot AC=AH^2\left(2\right)\)

Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)