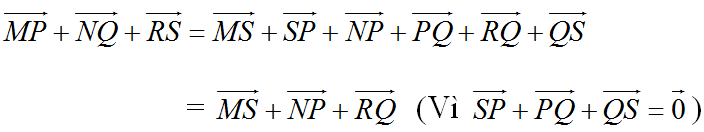\(|\overrightarrow{NP}+2\overrightarrow{NQ}|min\)

Những câu hỏi liên quan
trong mp Oxy cho đường tròn (C):(x-1)2+(y+4)2=25.
cho P(5;10), Q(8;1).tìm N thuộc (C) sao cho\(|\overrightarrow{NP}+2\overrightarrow{NQ}|\)min
Giải trâu bò:
Gọi \(N\left(x;y\right)\Rightarrow\left(x-1\right)^2+\left(y+4\right)^2=25\)
\(\left\{{}\begin{matrix}\overrightarrow{NP}=\left(5-x;10-y\right)\\2\overrightarrow{NQ}=\left(16-2x;2-2y\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{NP}+2\overrightarrow{NQ}=3.\left(7-x;4-y\right)\)
\(\Rightarrow A=\left|\overrightarrow{NP}+2\overrightarrow{NQ}\right|=3\sqrt{\left(x-7\right)^2+\left(y-4\right)^2}\)
\(A_{min}\) khi \(B=\left(x-7\right)^2+\left(y-4\right)^2\) đạt min
Lượng giác hóa:
Từ giả thiết \(\left(x-1\right)^2+\left(y+4\right)^2=25\Rightarrow\left(\frac{x-1}{5}\right)^2+\left(\frac{y+4}{5}\right)^2=1\)
\(\Rightarrow\) Đặt \(\left\{{}\begin{matrix}\frac{x-1}{5}=sina\\\frac{y+4}{5}=cosa\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=5sina+1\\y=5cosa-4\end{matrix}\right.\) thế vào B:
\(B=\left(5sina-6\right)^2+\left(5cosa-8\right)^2\)
\(B=25sin^2a+25cos^2a-60sina-80cosa+100\)
\(B=125-100\left(\frac{3}{5}sina+\frac{4}{5}cosa\right)=125-100.sin\left(a+\alpha\right)\)
\(\Rightarrow B_{min}=25\) khi \(sin\left(a+\alpha\right)=1\) \(\Rightarrow\left\{{}\begin{matrix}sina=\frac{3}{5}\\cosa=\frac{4}{5}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=5sina+1=4\\y=5cosa-4=0\end{matrix}\right.\) \(\Rightarrow N\left(4;0\right)\)
Đúng 0
Bình luận (0)
Cho 6 điểm M, N, P, Q, R, S bất kì. Chứng minh rằng :
\(\overrightarrow{MP}+\overrightarrow{NQ}+\overrightarrow{RS}=\overrightarrow{MS}+\overrightarrow{NP}+\overrightarrow{RQ}\)
Cho M,N,P,Q
C/m nếu :
a) \(\overrightarrow{MN}=\overrightarrow{PQ}\)thì \(\overrightarrow{MP}=\overrightarrow{NQ}\)
b) \(\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{QP}+\overrightarrow{MQ}\)
c) \(\overrightarrow{MN}+\overrightarrow{PQ}=\overrightarrow{MQ}+\overrightarrow{PN}\)
Cho tam giác ABC. Gọi M là trung điểm của BC. Trên cạnh AB,AC lần lượt lấy các điểm P,Q sao cho \(\overrightarrow{AP}=\dfrac{3}{4}\overrightarrow{AB},\overrightarrow{AQ}=\dfrac{2}{3}\overrightarrow{AC}\). Gọi N là giao điểm của AM và PQ. Đặt \(\overrightarrow{NP}=k\overrightarrow{NQ}\).Tìm k
Cm
1) overrightarrow{PQ}+overrightarrow{NP}+overrightarrow{MN}overrightarrow{MQ}
2)overrightarrow{NP}+overrightarrow{MN}overrightarrow{QP}+overrightarrow{MQ}
3)overrightarrow{MN}+overrightarrow{PQ}overrightarrow{MQ}+overrightarrow{PN}
4)overrightarrow{MN}+overrightarrow{PQ}+overrightarrow{QM}+overrightarrow{NP}overrightarrow{O}
5)overrightarrow{AB}-overrightarrow{CD}overrightarrow{AC}+overrightarrow{DB}
6)overrightarrow{AD}+overrightarrow{BE}+overrightarrow{CF}overrightarrow{AE}+overrighta...
Đọc tiếp
Cm
1) \(\overrightarrow{PQ}+\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{MQ}\)
2)\(\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{QP}+\overrightarrow{MQ}\)
3)\(\overrightarrow{MN}+\overrightarrow{PQ}=\overrightarrow{MQ}+\overrightarrow{PN}\)
4)\(\overrightarrow{MN}+\overrightarrow{PQ}+\overrightarrow{QM}+\overrightarrow{NP}=\overrightarrow{O}\)
5)\(\overrightarrow{AB}-\overrightarrow{CD}=\overrightarrow{AC}+\overrightarrow{DB}\)
6)\(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{AE}+\overrightarrow{BF}\)
7)\(\overrightarrow{AD}-\overrightarrow{FC}-\overrightarrow{EB}=\overrightarrow{CD}-\overrightarrow{EA}-\overrightarrow{FB}\)
8)\(\overrightarrow{AB}-\overrightarrow{DC}-\overrightarrow{FE}=\overrightarrow{CF}-\overrightarrow{DA}+\overrightarrow{EC}\)
1. Cho tứ giác MNPQ. CMR:
a) \(\overrightarrow{PQ}+\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{MQ}\)
b)\(\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{QP}+\overrightarrow{MQ}\)
Dễ mà bạn :)) cái này dùng qui tắc công với chèn điểm là nuột =)
a) \(\overrightarrow{PQ}+\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{NP}+\overrightarrow{PQ}+\overrightarrow{MN}\)
\(=\overrightarrow{NQ}+\overrightarrow{MN}=\overrightarrow{MN}+\overrightarrow{NQ}=\overrightarrow{MQ}\left(đpcm\right)\)
( quá chi tiết rồi nha bạn... )
b) Ta có: \(\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{NQ}+\overrightarrow{QP}+\overrightarrow{MQ}+\overrightarrow{QN}\)
\(\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{QP}+\overrightarrow{MQ}+\overrightarrow{NQ}+\overrightarrow{QN}\)
\(\Rightarrow\overrightarrow{NP}+\overrightarrow{MN}=\overrightarrow{QP}+\overrightarrow{MQ}\left(đpcm\right)\)
Đúng 0
Bình luận (0)
Cho hình thang MNPQ, MN // PQ, MN = 2PQ. Phát biểu nào sau đây là đúng?
A. \(\overrightarrow {MN} = 2\overrightarrow {PQ} \)
B. \(\overrightarrow {MN} = 2\overrightarrow {NP} \)
C. \(\overrightarrow {MN} = - 2\overrightarrow {PQ} \)
D. \(\overrightarrow {MQ} = - 2\overrightarrow {NP} \)
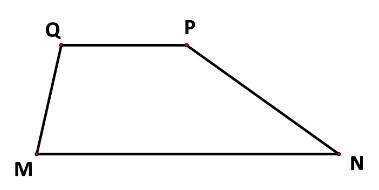
Do MQ và PN không song song với nhau nên \(\overrightarrow {MQ} \ne k\overrightarrow {NP} \). Vậy loại B và D.
Ta có: \(\overrightarrow {MN} ,\overrightarrow {PQ} \)là hai vecto ngược hướng và \(\left| {\overrightarrow {MN} } \right| = 2\left| {\overrightarrow {PQ} } \right|\)
Suy ra \(\overrightarrow {MN} = - 2\overrightarrow {PQ} \)
Vậy chọn C.
Đúng 1
Bình luận (0)
Cho ba điểm M, N, P. Vecto \(\overrightarrow u = \overrightarrow {NP} + \overrightarrow {MN} \) bằng vecto nào sau đây?
A. \(\overrightarrow {PN} \)
B. \(\overrightarrow {PM} \)
C. \(\overrightarrow {MP} \)
D. \(\overrightarrow {NM} \)
Vận dụng tính chất giao hoán ta có: \[\overrightarrow u = \overrightarrow {NP} + \overrightarrow {MN} = \overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP} \]
Chọn C.
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Dựng \(\overrightarrow{AM}=\overrightarrow{BA};\overrightarrow{MN}=\overrightarrow{DA};\overrightarrow{NP}=\overrightarrow{DC};\overrightarrow{PQ}=\overrightarrow{BC}\). Chứng minh \(\overrightarrow{AQ}=\overrightarrow{0}\) ?
Do \(\overrightarrow{NP}=\overrightarrow{DC}\); \(\overrightarrow{AM}=\overrightarrow{BA}\Rightarrow\overrightarrow{MA}=\overrightarrow{AB}\).
Do tứ giác ABCD là hình bình hành nên \(\overrightarrow{AB}=\overrightarrow{DC}\).
Vì vậy \(\overrightarrow{NP}=\overrightarrow{MA}\) nên tứ giác NPAM là hình bình hành.
Vì vậy \(\overrightarrow{PA}=\overrightarrow{NM}\). (1)
Mà \(\overrightarrow{MN}=\overrightarrow{DA}\) suy ra \(\overrightarrow{NM}=\overrightarrow{AD}\) . (2)
Mặt khác \(\overrightarrow{AD}=\overrightarrow{BC}\) (do tứ giác ABCD là hình bình hành). (3)
Từ (1);(2);(3) suy ra:\(\overrightarrow{PA}=\overrightarrow{BC}\).
Mà \(\overrightarrow{PQ}=\overrightarrow{BC}\Rightarrow\overrightarrow{PQ}=\overrightarrow{PA}\).
Vì vậy hai điểm A và Q trùng nhau nên \(\overrightarrow{AQ}=\overrightarrow{0}\).
Đúng 0
Bình luận (0)