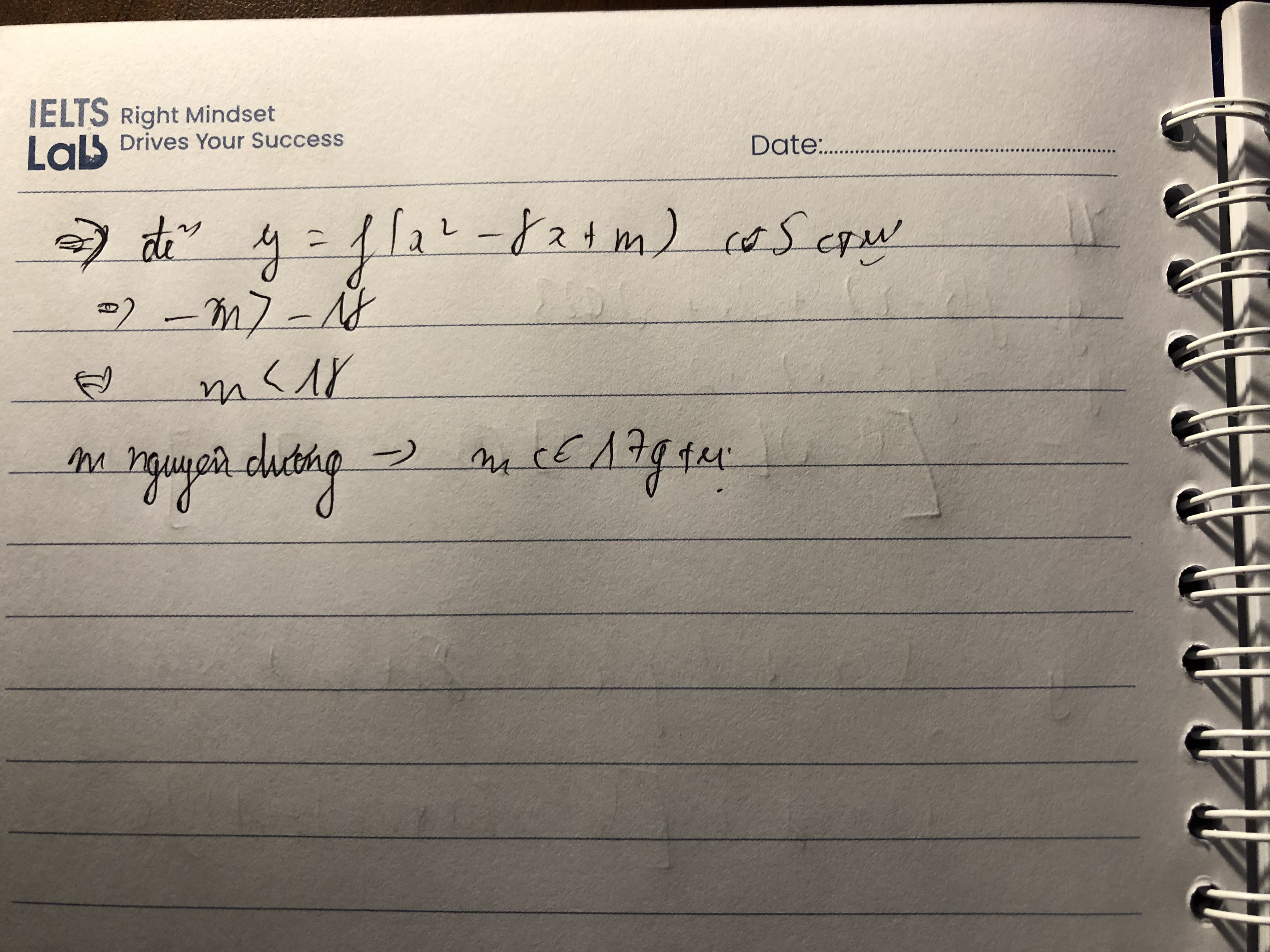Cho y=a\(\left|X+3\right|\)+b\(\left|X+2\right|\)+cx là hàm số tăng thêm R. Chứng minh c>0

Những câu hỏi liên quan
Câu 48: Cho hàm số yf(x) có đạo hàm liên tục trên R và fleft(xright)xleft(2x-1right)left(x^2+3right)+2. Hàm số yfleft(3-xright)+2x+2023 đồng biến trên khoảng nào trong các khoảng sau?A: left(-infty;3right)B: (3;5)C: (2;5/2)D: (5/2;3)Câu 50: Cho hàm số yf(x) có đạo hàm fleft(xright)left(x-1right)^2cdotleft(x^2-2xright) với forall xin R. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số fleft(x^2-8x+mright) có 5 điểm cực trị?
Đọc tiếp
Câu 48: Cho hàm số y=f(x) có đạo hàm liên tục trên R và \(f'\left(x\right)=x\left(2x-1\right)\left(x^2+3\right)+2\). Hàm số \(y=f\left(3-x\right)+2x+2023\) đồng biến trên khoảng nào trong các khoảng sau?
A: \(\left(-\infty;3\right)\)
B: (3;5)
C: (2;5/2)
D: (5/2;3)
Câu 50: Cho hàm số y=f(x) có đạo hàm \(f'\left(x\right)=\left(x-1\right)^2\cdot\left(x^2-2x\right)\) với \(\forall x\in R\). Có bao nhiêu giá trị nguyên dương của tham số m để hàm số \(f\left(x^2-8x+m\right)\) có 5 điểm cực trị?
Cho hàm số y = f(x) liên tục trên R và f(0) = f(1). Chứng minh phương trình \(f\left(x+\dfrac{1}{3}\right)-f\left(x\right)=0\) luôn có nghiệm thuộc đoạn [0;1]
Đặt \(g\left(x\right)=f\left(x+\dfrac{1}{3}\right)-f\left(x\right)\)
Hiển nhiên \(g\left(x\right)\) cũng liên tục trên R
Ta có: \(g\left(0\right)=f\left(\dfrac{1}{3}\right)-f\left(0\right)\)
\(g\left(\dfrac{2}{3}\right)=f\left(1\right)-f\left(\dfrac{2}{3}\right)\)
\(g\left(\dfrac{1}{3}\right)=f\left(\dfrac{2}{3}\right)-f\left(\dfrac{1}{3}\right)\)
Cộng vế với vế:
\(g\left(0\right)+g\left(\dfrac{1}{3}\right)+g\left(\dfrac{2}{3}\right)=f\left(1\right)-f\left(0\right)=0\)
- Nếu tồn tại 1 trong 3 giá trị \(g\left(0\right);g\left(\dfrac{1}{3}\right);g\left(\dfrac{2}{3}\right)\) bằng 0 thì hiển nhiên pt có nghiệm
- Nếu cả 3 giá trị đều khác 0 \(\Rightarrow\) tồn tại ít nhất 2 trong 3 giá trị \(g\left(0\right)\) ; \(g\left(\dfrac{1}{3}\right)\) ; \(g\left(\dfrac{2}{3}\right)\) trái dấu
\(\Rightarrow\) Luôn tồn tại ít nhất 1 trong 3 tích số: \(g\left(0\right).g\left(\dfrac{1}{3}\right)\) ; \(g\left(0\right).g\left(\dfrac{2}{3}\right)\) ; \(g\left(\dfrac{1}{3}\right).g\left(\dfrac{2}{3}\right)\) âm
\(\Rightarrow\) Pt \(g\left(x\right)=0\) luôn có ít nhất 1 nghiệm thuộc \(\left[0;1\right]\)
Đúng 5
Bình luận (1)
Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{\frac{{{x^2} - 2x}}{x}}&{khi\,\,x \ne 0}\\a&{khi\,\,x = 0}\end{array}} \right.\).
Tìm \(a\) để hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\).
Trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\), \(f\left( x \right) = \frac{{{x^2} - 2x}}{x}\) là hàm phân thức hữu tỉ nên liên tục trên từng khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\).
Ta có: \(f\left( 0 \right) = a\)
\(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = \mathop {\lim }\limits_{x \to 0} \frac{{{x^2} - 2x}}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{x\left( {x - 2} \right)}}{x} = \mathop {\lim }\limits_{x \to 0} \left( {x - 2} \right) = 0 - 2 = - 2\)
Để hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) thì hàm số \(y = f\left( x \right)\) phải liên tục tại điểm \({x_0} = 0\). Khi đó:
\(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = f\left( 0 \right) \Leftrightarrow a = - 2\).
Vậy với \(a = - 2\) thì hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\).
Đúng 0
Bình luận (0)
Cho hàm số \(f\left(x\right)=ax^3+bx^2+cx+d\) thỏa mãn \(f\left(-1\right)=2,f\left(0\right)=1,f\left(1\right)=7,f\left(\dfrac{1}{2}\right)=3\). Xác định giá trị \(a,b,c,d\).
\(f\left(-1\right)=2\Rightarrow-a+b-c+d=2\\ f\left(0\right)=1\Rightarrow d=1\\ f\left(1\right)=7\Rightarrow a+b+c+d=7\\ f\left(\dfrac{1}{2}\right)=3\Rightarrow\dfrac{1}{8}a+\dfrac{1}{4}b+\dfrac{1}{2}c+d=3\)
\(d=1\Rightarrow-a+b-c=1;a+b+c=6\\ \Rightarrow2b=7\\ \Rightarrow b=\dfrac{7}{2}\\ \Rightarrow\dfrac{1}{8}a+\dfrac{7}{8}+\dfrac{1}{2}c=2\\ \Rightarrow\dfrac{1}{2}\left(\dfrac{1}{4}a+\dfrac{7}{4}+c\right)=2\\ \Rightarrow\dfrac{1}{4}a+\dfrac{7}{4}+c=4\\ \Rightarrow a+7+4c=16\\ \Rightarrow a+4c=9;a+c=6-\dfrac{7}{2}=\dfrac{5}{2}\\ \Rightarrow3c=\dfrac{13}{2}\Rightarrow c=\dfrac{13}{6}\\ \Rightarrow a=\dfrac{5}{2}-\dfrac{13}{6}=\dfrac{1}{3}\)
Vậy \(\left(a;b;c;d\right)=\left(\dfrac{1}{3};\dfrac{7}{2};\dfrac{13}{6};1\right)\)
Đúng 4
Bình luận (0)
Quan sát đồ thị của hàm số yfleft(xright)-x^2 trên R (H.6.5). Hỏi:a) Giá trị của fleft(xright) tăng hay giảm khi x tăng trên khoảng left(-infty;0right)?b) Giá trị của fleft(xright) tăng hay giảm khi x tăng trên khoảng left(0;+inftyright)?
Đọc tiếp
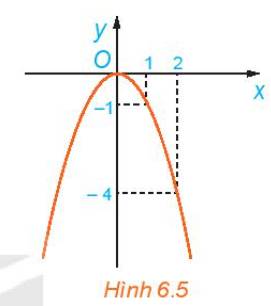
Quan sát đồ thị của hàm số \(y=f\left(x\right)=-x^2\) trên \(R\) (H.6.5).
Hỏi:
a) Giá trị của \(f\left(x\right)\) tăng hay giảm khi x tăng trên khoảng \(\left(-\infty;0\right)\)?
b) Giá trị của \(f\left(x\right)\) tăng hay giảm khi x tăng trên khoảng \(\left(0;+\infty\right)\)?
Dựa vào đồ thị, ta thấy:
a) Trên khoảng \(\left( { - \infty ;0} \right)\) , giá trị của f(x) tăng
b) Trên khoảng \(\left( {0; + \infty } \right)\) , giá trị của f(x) giảm
Đúng 0
Bình luận (0)
Cho hàm số \(f\left(x\right)\) có đồ thị \(f'\left(x\right)=\left(e^x-1\right)\left(x^2-x-2\right)\)với mọi \(x\in R\).Số điểm cực tiểu của hàm số đã cho là
A. 0.
B. 1.
C. 2.
D. 3
\(f'\left(x\right)=0\) có 3 nghiệm \(x=-1;0;2\)
Dấu của \(f'\left(x\right)\) trên trục số:
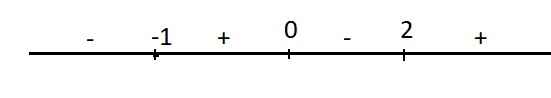
Ta thấy có 2 lần \(f'\left(x\right)\) đổi dấu từ âm sang dương nên hàm có 2 cực tiểu
Đúng 2
Bình luận (0)
Tìm tất cả hàm số \(f:R\rightarrow R\) thoả mãn:
\(f\left(xf\left(y\right)-y\right)+f\left(xy-x\right)+f\left(x+y\right)=2xy,\forall x,y\in R\)
Em chỉ mới chứng minh được f là hàm lẻ ạ, mong mọi người giúp :'(
Thay \(x=0;y=0\) vào giả thiết ta được \(f\left(0\right)=0\)
Thay \(y=0\) ta được \(f\left(x\right)+f\left(-x\right)=0\Rightarrow f\) là hàm lẻ
(Phân tích 1 chút: khi đã có hàm lẻ, ta cần thế tiếp 1 cặp sao cho "khử" được biểu thức phức tạp dạng hàm lồng đầu tiên, bằng cách tìm 1 giá trị y sao cho: \(x.f\left(y\right)-y=-\left(x+y\right)\) hoặc là \(x.f\left(y\right)-y=-\left(xy-x\right)\). Cái thứ nhất cho ta \(x.\left[f\left(y\right)+1\right]=0\Rightarrow f\left(y\right)=-1\) , nghĩa là ta chỉ cần tìm 1 hằng số c sao cho \(f\left(c\right)=-1\). Cái thứ 2 ko cho điều gì tốt nên bỏ qua. Bây giờ ta đi tìm c. Vế phải cần bằng -1, nghĩa là \(xy=-\dfrac{1}{2}\), vế trái cần khử bớt 2 số hạng. Nhưng trước khi có c thì \(f\left(x.f\left(y\right)-y\right)\) chưa khử được, nên ta cần khử cặp sau, bằng cách cho \(xy-x=-\left(x+y\right)\Rightarrow xy=-y\Rightarrow x=-1\), thay vào \(xy=-\dfrac{1}{2}\Rightarrow y=\dfrac{1}{2}\). Xong.)
Thế \(x=-1;y=\dfrac{1}{2}\) ta được:
\(f\left(-f\left(\dfrac{1}{2}\right)-\dfrac{1}{2}\right)+f\left(-\dfrac{1}{2}+1\right)+f\left(-1+\dfrac{1}{2}\right)=-1\)
\(\Leftrightarrow f\left(-f\left(\dfrac{1}{2}\right)-\dfrac{1}{2}\right)=-1\)
Đặt \(c=-f\left(\dfrac{1}{2}\right)-\dfrac{1}{2}\) là 1 hằng số nào đó
\(\Rightarrow f\left(c\right)=-1\)
Thế \(y=c\) vào ta được:
\(f\left(x.f\left(c\right)-c\right)+f\left(cx-x\right)+f\left(x+c\right)=2c.x\)
\(\Leftrightarrow f\left(-x-c\right)+f\left(x+c\right)+f\left(cx-x\right)=2c.x\)
\(\Leftrightarrow f\left(cx-x\right)=2c.x\) (1)
- Nếu \(c=1\Rightarrow f\left(0\right)=2x\) ko thỏa mãn \(f\left(0\right)=0\)
\(\Rightarrow c\ne1\), khi đó đặt \(cx-x=t\) \(\Rightarrow x=\dfrac{t}{c-1}\)
(1) trở thành \(f\left(t\right)=\dfrac{2c}{c-1}.t\)
Đặt \(\dfrac{2c}{c-1}=a\) \(\Rightarrow f\left(t\right)=a.t\)
Hay hàm cần tìm có dạng \(f\left(x\right)=ax\) với a là hằng số
Đúng 3
Bình luận (2)
Cho hàm số y =f(x)=ax+b. Biết \(f\left(3\right)\le f\left(1\right)\le f\left(2\right)\)và f(4)=2. Chứng minh rằng: a=0 và f(0)=2
Cho ba số phân biệt a,b,c \(\in\) R. Chứng minh rằng phương trình:
\(\left(x-a\right)\left(x-b\right)+\left(x-b\right)\left(x-c\right)+\left(x-c\right)\left(x-a\right)=0\) luôn có hai nghiệm phân biệt