Cho M thuộc (P) : y= \(^{x^2}\)và A( 3;0) ,Để AM ngắn nhất thì :
A. M ( 1;1) B . M ( -1;1) C . M ( 1;-1) D. M (-1 ;-1)
Những câu hỏi liên quan
1/ Cho:
x thuộc { -3 ; -2 ; -1 ; 0 ; 1 ; 2 ; .... ; 10 }
y thuộc {-1 ; 0 ; 1 ; .... ;5 }
Biết : x + y = 3, tìm x và y
2/ Cho
S1 = 1 + (-3) + 5 + (-7) + ..... + 17
S2 = -2 + 4 + (-6) + 8 + .... + (-18)
Tính S1 + S2
3/ Cho M = {-94 ; -24 ;-1 ; -9 ; -31} và a, b thuộc M
Tính giá trị nhỏ nhất của a + b, giá trị lớn nhất của a + b
Cho 3 nguyên tố X, Y, M thuộc nhóm A của bảng tuần hoàn. X, Y cùng một chu kì và thuộc hai nhóm liên tiếp. M, X thuộc cùng một nhóm và ở hai chu kì liên tiếp. Tính kim loại: M > X > Y. Nguyên tử của nguyên tố X có 2 electron lớp ngoài cùng thuộc phân lớp 3s.
a. Viết cấu hình electron nguyên tử của X, Y, M.
b. Viết công thức hiđroxit ứng với oxit bậc cao nhất của Y.
a,Chứng minh nếu m và n là 2 stn thì B=(m+2n+3).(3m-2n-2) là số chẵn
b,cho x,y thuộc Z
A=3x(x-y)và B=y2-x2 biết x-y chia hết cho 7
chứng minh A-B chia hết cho 7
1. Cho hàm số y2x-1/x-1 . Lấy M thuộc C với XMm . tiếp tuyến của C tại M cắt 2 đường tiệm cận tại A,B . Gọi I là giao của 2 đường tiệm cận . CMR : M là trung điểm của AB và tam giác IAB có diện tích không phụ thuộc vào M 2.cho yx+2/x-3 tìm M thuộc C sao cho khoảng cách từ M đến 2 đường tiệm cận C bằng nhau 3. cho y x+2/x-2 tìm M thuộc C sao cho M cách đều hai trục tọa độ . viết pttt của C biết tiếp tuyến đó đi qua A(-6;5) 4 . cho y x+1/x-1 . CMR (d) : 2x-y+m0 luôn cắt C tại A,B trên 2 nhánh củ...
Đọc tiếp
1. Cho hàm số y=2x-1/x-1 . Lấy M thuộc C với XM=m . tiếp tuyến của C tại M cắt 2 đường tiệm cận tại A,B . Gọi I là giao của 2 đường tiệm cận . CMR : M là trung điểm của AB và tam giác IAB có diện tích không phụ thuộc vào M
2.cho y=x+2/x-3 tìm M thuộc C sao cho khoảng cách từ M đến 2 đường tiệm cận C bằng nhau
3. cho y = x+2/x-2 tìm M thuộc C sao cho M cách đều hai trục tọa độ . viết pttt của C biết tiếp tuyến đó đi qua A(-6;5)
4 . cho y = x+1/x-1 . CMR (d) : 2x-y+m=0 luôn cắt C tại A,B trên 2 nhánh của (C) . tìm m để AB ngắn nhất
Cho tam giác ABC đều
D thuộc AB , E thuộc AC sao cho BD = AE
CM : Khi D,E thay đổi ( di chuyển ) trên AB,AC thì đường trung tuyến DE luôn đi qua điểm cố định
Help me !!!
Đúng 0
Bình luận (0)
Cho parabol (P): y = -x^2 và đường thẳng (d): y = mx + 2
a)tìm m để (d) cắt (P) tại 1 điểm duy nhất
b)Cho 2 điểm A(-2,m) và B(1,m).Tìm m,n để A thuộc (P) và B thuộc (d)
a: Phương trình hoành độ giao điểm là:
\(-x^2-mx-2=0\)
\(\Leftrightarrow x^2+mx+2=0\)
\(\Delta=m^2-8\)
Để (P) cắt (d) tại 1 điểm duy nhất thì Δ=0
hay \(m\in\left\{2\sqrt{2};-2\sqrt{2}\right\}\)
b: Thay x=-2 vào (P), ta được:
\(y=-\left(-2\right)^2=-4\)
hay m=-4
Đúng 1
Bình luận (0)
1) Cho A = 7+x / x-3
a, Tìm x thuộc Z để A là phân số
b, Tìm x thuộc Z để A là số nguyên
2) Tìm x,y thuộc Z :
a, x/5 = 2/y
b, x/7 = y/8 và y - x = 2
c, x/3 = y/4 và x + 2y = 22
1)a, Để A là phân số thì: \(\left\{{}\begin{matrix}7+x\in Z\Rightarrow x\in Z\\x-3\in Z\Rightarrow x\in Z\\x-3\ne0\Rightarrow x\ne3\end{matrix}\right.\)
Vậy: Để A là phân số thì: x \(\in\) Z; x \(\ne\) 3
b, Để A là số nguyên thì: 7+x \(⋮\) x-3
\(\Leftrightarrow x-3+10⋮x-3\)
Vì x-3 \(⋮\) x-3 nên: 10 \(⋮\) x-3
\(\Rightarrow x-3\inƯ\left(10\right)=\left\{1;2;5;10;-1;-2;-5;-10\right\}\)
\(\Rightarrow x\in\left\{........\right\}\)( Bạn tự làm nốt nha)
Vậy:..................
Đúng 0
Bình luận (0)
Cho A = { 1 ; 2 ; 3 ; 4 , a , b , x , y } và B = { 7 ; 3 ; 4 , s , a , y , t }
( a ) Gọi M là tập hợp gồm các phần tử vừa thuộc A vừa thuộc B . Viết tập hợp M
( b ) Tập hợp M có bao nhiêu phần tử ?
( a ) M = A ∩ B = {3 ; 4 ; a ; y}
( b ) Tập hợp M có 4 phần tử
1. tìm GTNN của A = |3x +1| + |3x-1|
2. tìm x, y thuộc Q sao cho: x+y = x*y = x/y
3. cho x, y thuộc Q chứng minh |x| +|y| > |x+y|
cho pt đtron (C): (x+3)^2 + (y-2)^2=4 và ?(C’): x^2 +y^2 -2x +4y -4=0 Tìm tọa độ M thuộc (C) sao cho qua M kẻ tiếp tuyến MA, MB đến (C’) với B,A là tiếp điểm và góc AMB=60 độ.
cho hàm số yx2+ x- 2��2−2�+3 có đồ thị (P) và ��2−2�+3(d): y - (m + 1)x + m + 2a. xét sự biến thiên và vẽ (P)b. có bao nhiên giá trị m nguyên thuộc [-10; 4] để d cắt P tại 2 điểm A; B nằm về cùng phía trục Oy
Đọc tiếp
cho hàm số + có đồ thị (P) và (d): y = - (m + 1)x + m + 2
a. xét sự biến thiên và vẽ (P)
b. có bao nhiên giá trị m nguyên thuộc [-10; 4]
để d cắt P tại 2 điểm A; B nằm về cùng phía trục Oy
a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-b}{2a}=\dfrac{-1}{2}\\y=-\dfrac{b^2-4ac}{4a}=-\dfrac{1^2-4\cdot1\cdot\left(-2\right)}{4\cdot1}=-\dfrac{1+8}{4}=-\dfrac{9}{4}\end{matrix}\right.\)
Vì (P): \(y=x^2+x-2\) có a=1>0
nên (P) đồng biến khi x>-1/2 và nghịch biến khi x<-1/2
Vẽ (P):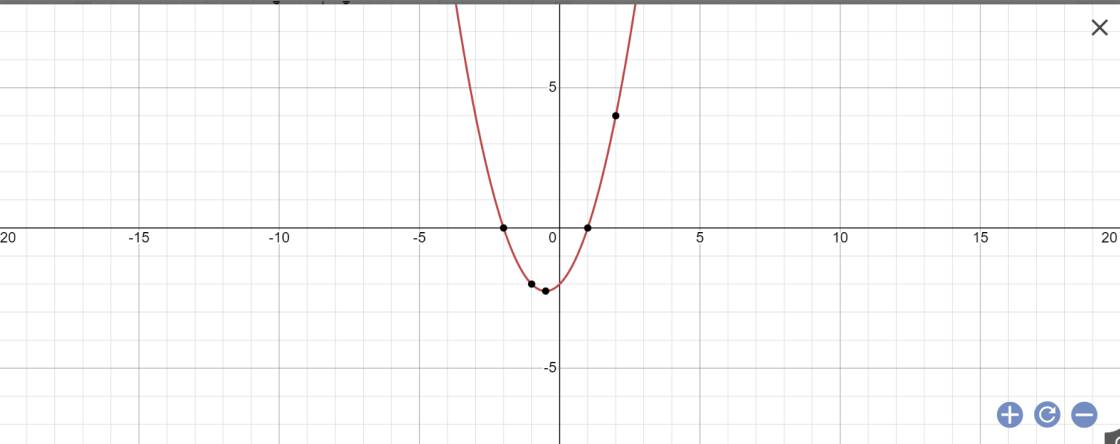 
b: Phương trình hoành độ giao điểm là:
\(x^2+x-2=-\left(m+1\right)x+m+2\)
=>\(x^2+x-2+\left(m+1\right)x-m-2=0\)
=>\(x^2+\left(m+2\right)x-m-4=0\)(1)
Để (P) cắt (d) tại hai điểm phân biệt A,B nằm về hai phía so với trục Oy thì phương trình (1) có hai nghiệm phân biệt trái dấu
=>-m-4<0
=>-m<4
=>m>-4
mà \(m\in Z;m\in\left[-10;4\right]\)
nên \(m\in\left\{-3;-2;-1;0;1;2;3;4\right\}\)
=>Có 8 số thỏa mãn
Đúng 1
Bình luận (0)