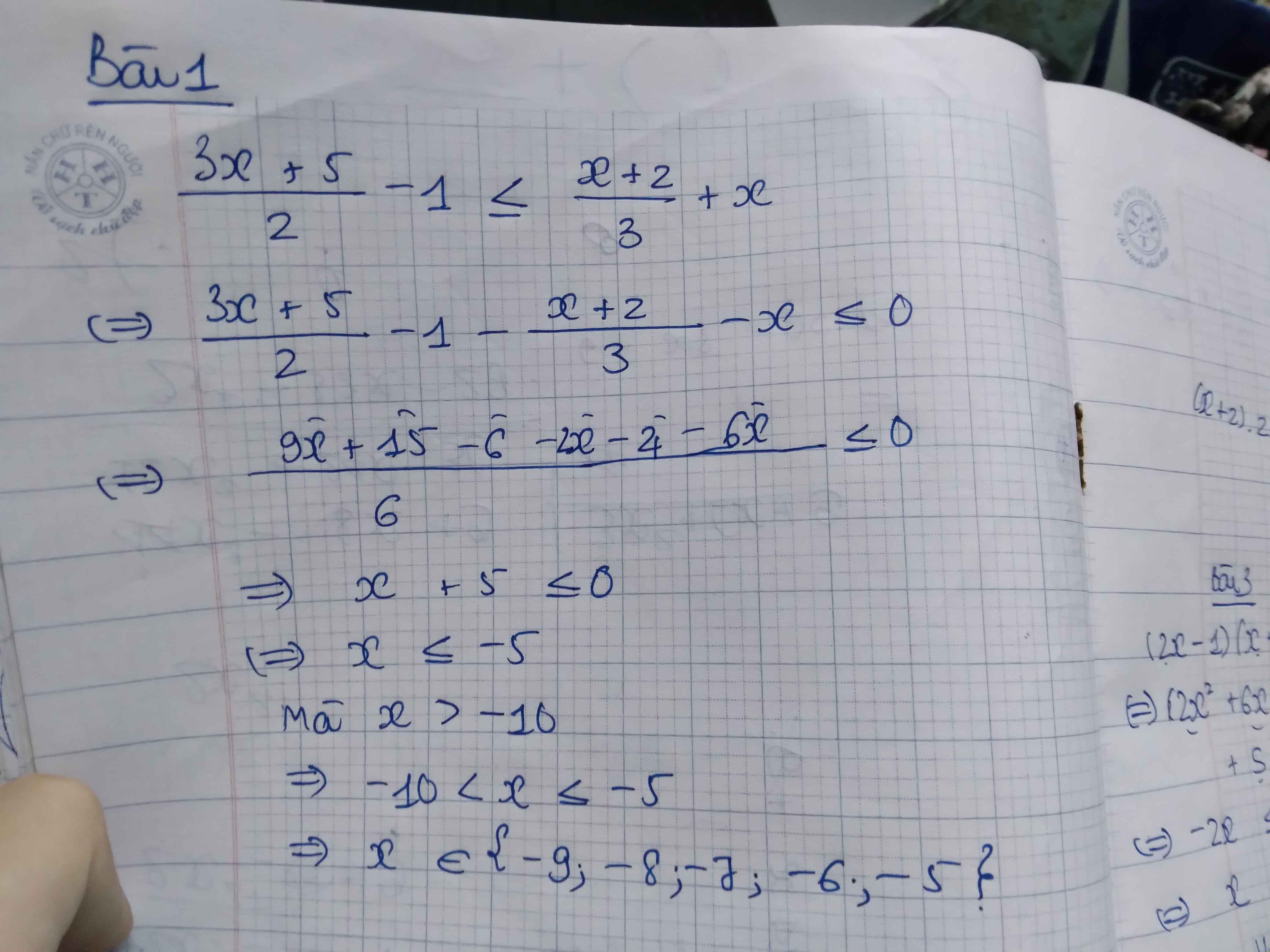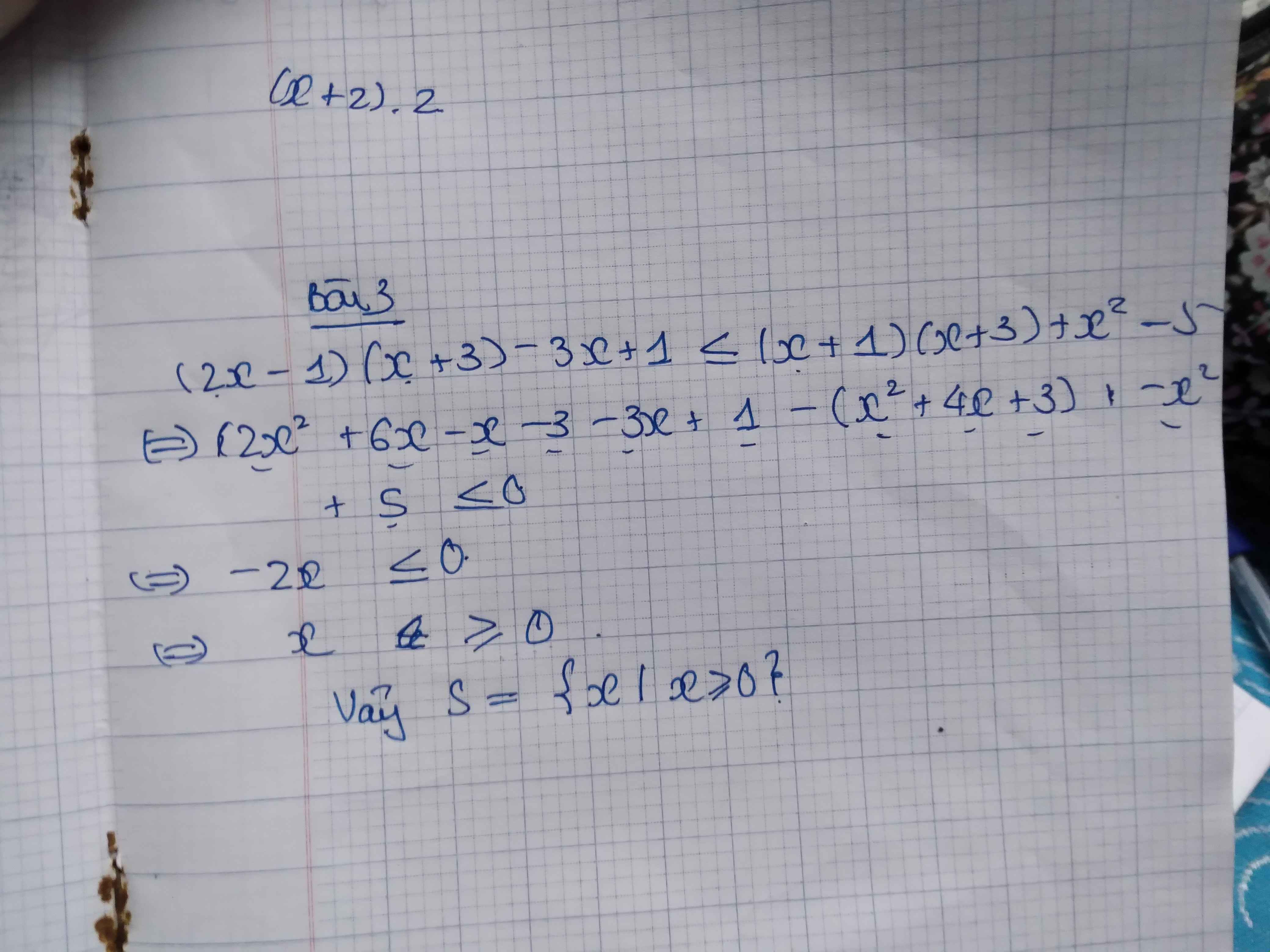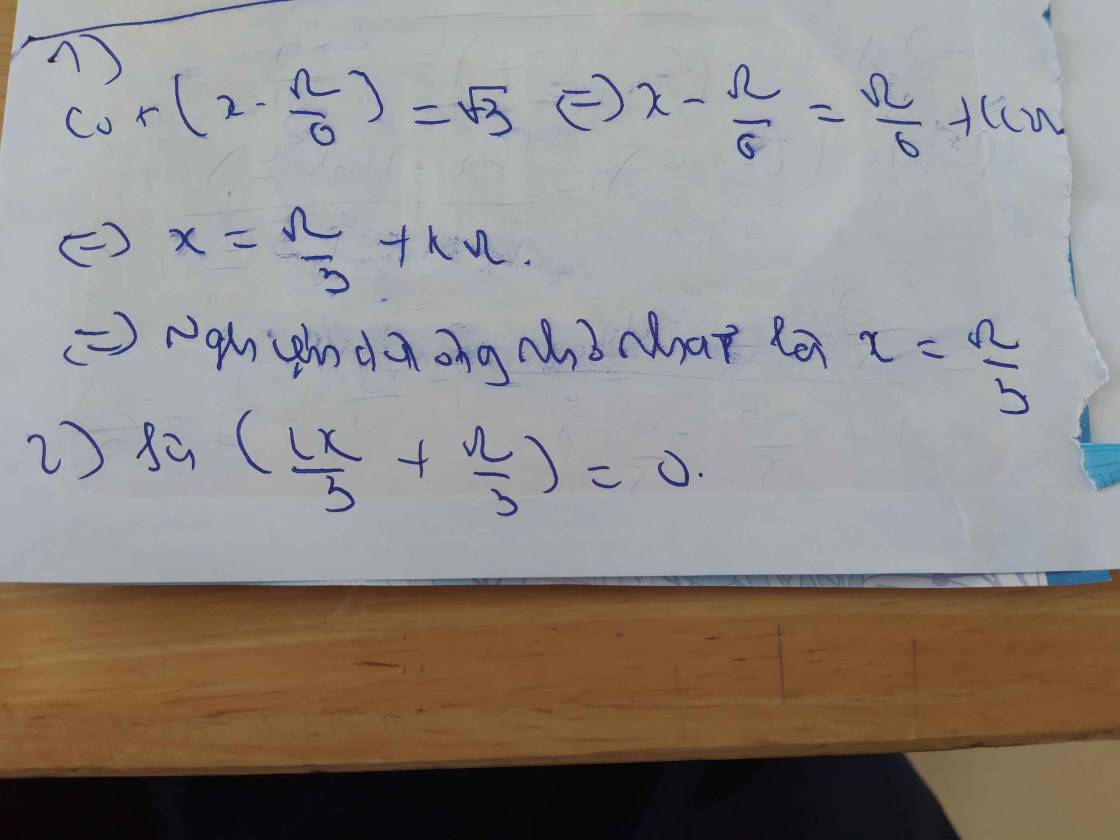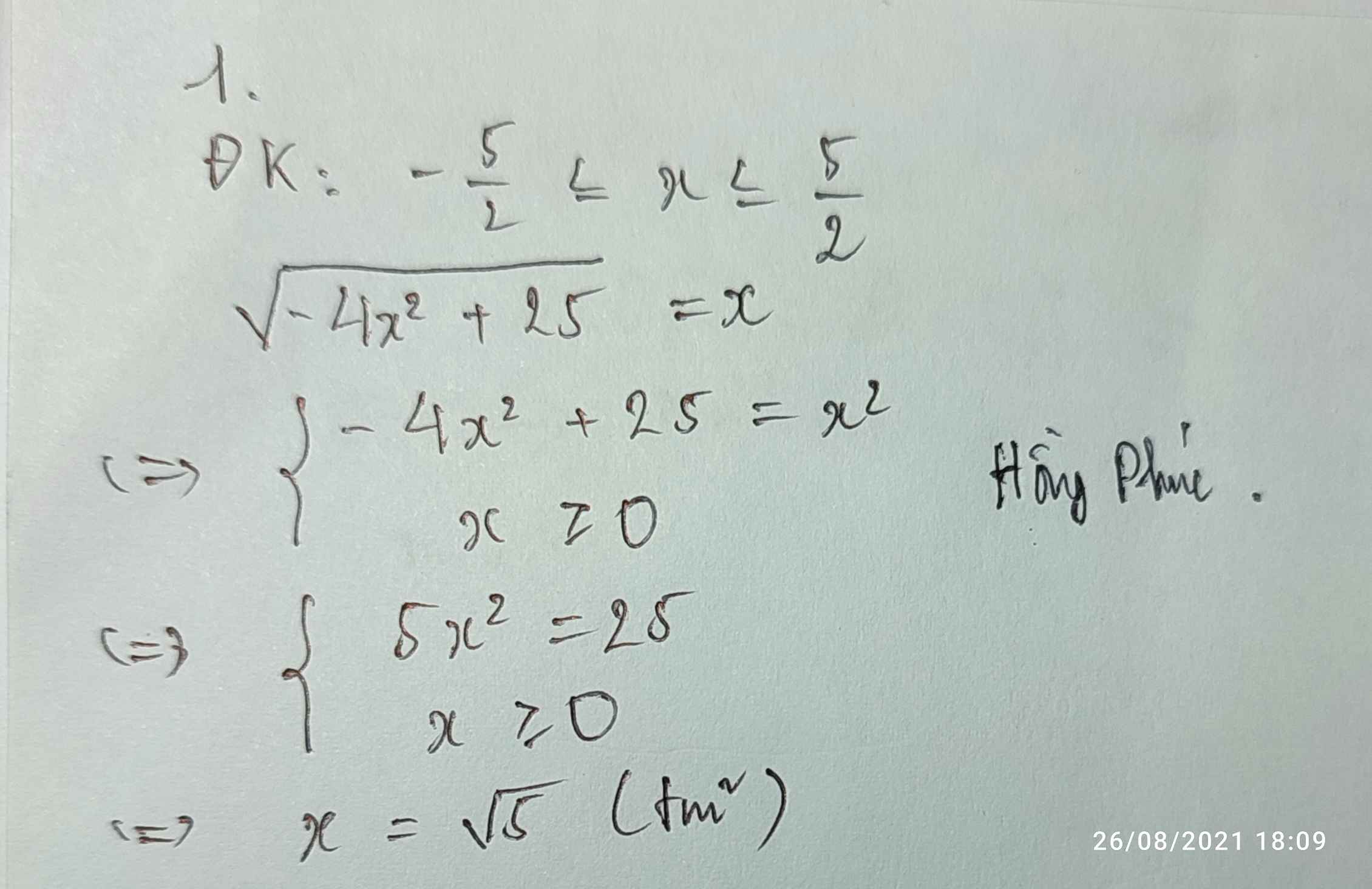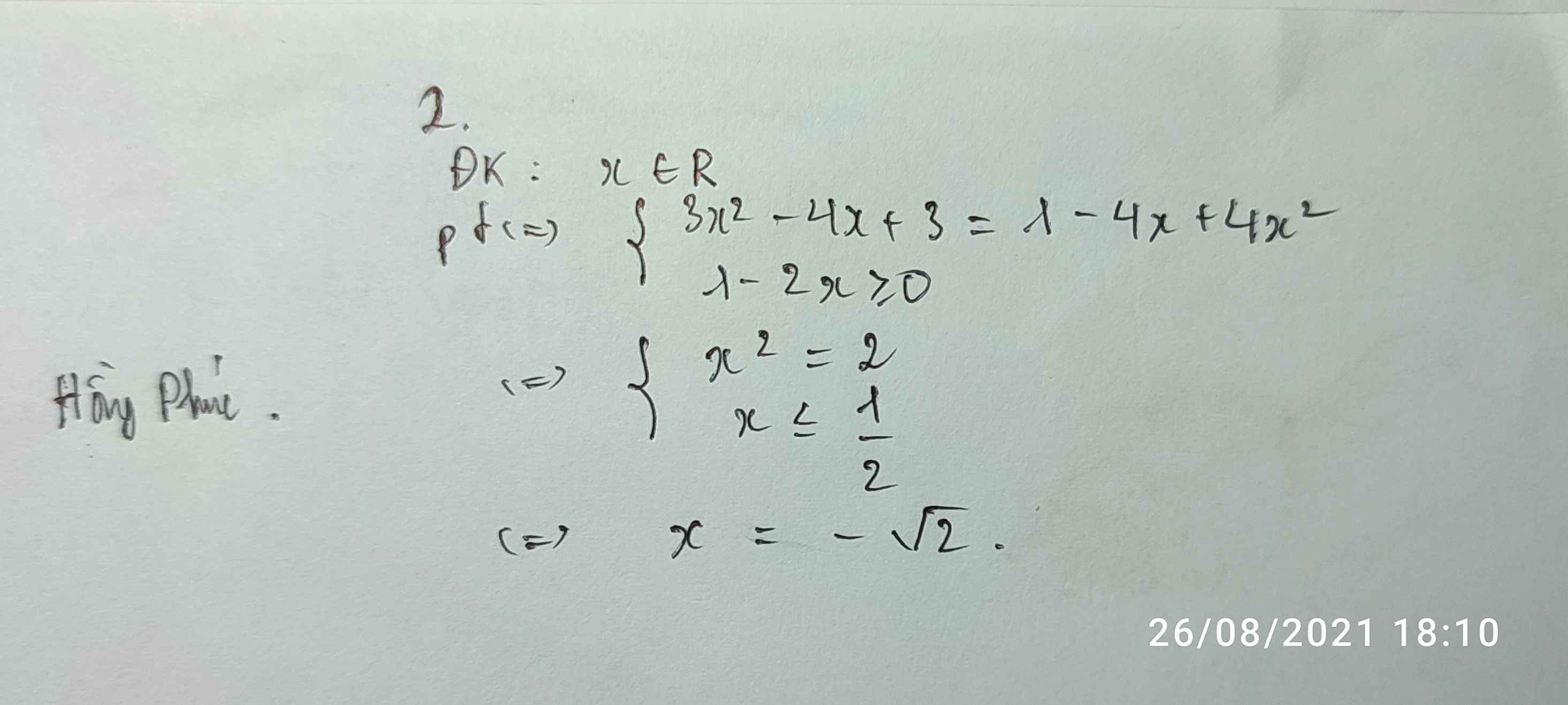(\(\dfrac{1}{2}\))-3x – 2.4x – 3.(\(\sqrt{2}\))2x = 0 có nghiệm là

Những câu hỏi liên quan
B1
\(\dfrac{3x+5}{2}-1\le\dfrac{x+2}{3}+x\)
Có bnhieu nghiệm nguyên lớn hơn -10
BÀI 2 . Tập nghiệm S của btp\(\left(1-\sqrt{2}\right)x< 3-2\sqrt{2}\)
BÀI 3 \(\left(2X-1\right)\left(x+3\right)-3x+1\le\left(x+1\right)\left(x+3\right)+x^2-5\) có tập nghiệm là?
Bài 1 :
Ta có : \(\dfrac{3x+5}{2}-1\le\dfrac{x+2}{3}+x\)
\(\Leftrightarrow\dfrac{3x+5}{2}-1-\dfrac{x+2}{3}-x\le0\)
\(\Leftrightarrow\dfrac{3\left(3x+5\right)-6-2\left(x+2\right)-6x}{6}\le0\)
\(\Leftrightarrow9x+15-6-2x-4-6x\le0\)
\(\Leftrightarrow x\le-5\)
Mà \(\left\{{}\begin{matrix}x\in Z\\x>-10\end{matrix}\right.\)
Vậy \(x\in\left\{-5;-6;-7;-8;-9\right\}\)
Đúng 2
Bình luận (0)
b3\(\Leftrightarrow2x^2+5x-3-3x+1\le x^2+2x-3+x^2-5\\ \Leftrightarrow0.x\le-6\Leftrightarrow x\in\varnothing\)
Đúng 0
Bình luận (0)
Giải các phương trình sau:1) sqrt{3x^2+5x+8}-sqrt{3x^2+5x+1}12) x^2-2x-12+4sqrt{left(4-xright)left(2+xright)}03) 3sqrt{x}+dfrac{3}{2sqrt{x}}2x+dfrac{1}{2x}-74) sqrt{x}-dfrac{4}{sqrt{x+2}}+sqrt{x+2}05)left(x-7right)sqrt{dfrac{x+3}{x-7}}x+46) 2sqrt{x-4}+sqrt{x-1}sqrt{2x-3}+sqrt{4x-16}7) sqrt{x+2sqrt{x-1}}+sqrt{x-2sqrt{x-1}}dfrac{x+3}{2}Giúp mình với ajk, mink đang cần gấp
Đọc tiếp
Giải các phương trình sau:
1) \(\sqrt{3x^2+5x+8}-\sqrt{3x^2+5x+1}=1\)
2) \(x^2-2x-12+4\sqrt{\left(4-x\right)\left(2+x\right)}=0\)
3) \(3\sqrt{x}+\dfrac{3}{2\sqrt{x}}=2x+\dfrac{1}{2x}-7\)
4) \(\sqrt{x}-\dfrac{4}{\sqrt{x+2}}+\sqrt{x+2}=0\)
5)\(\left(x-7\right)\sqrt{\dfrac{x+3}{x-7}}=x+4\)
6) \(2\sqrt{x-4}+\sqrt{x-1}=\sqrt{2x-3}+\sqrt{4x-16}\)
7) \(\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}=\dfrac{x+3}{2}\)
Giúp mình với ajk, mink đang cần gấp
Giải các phương trình, bất phương trình sau:
1) \(\sqrt{3x+7}-5< 0\)
2) \(\sqrt{-2x-1}-3>0\)
3) \(\dfrac{\sqrt{3x-2}}{6}-3=0\)
4) \(-5\sqrt{-x-2}-1< 0\)
5) \(-\dfrac{2}{3}\sqrt{-3-x}-3>0\)
1) \(\sqrt[]{3x+7}-5< 0\)
\(\Leftrightarrow\sqrt[]{3x+7}< 5\)
\(\Leftrightarrow3x+7\ge0\cap3x+7< 25\)
\(\Leftrightarrow x\ge-\dfrac{7}{3}\cap x< 6\)
\(\Leftrightarrow-\dfrac{7}{3}\le x< 6\)
Đúng 0
Bình luận (0)
giải các phương trình sau:1,sqrt{18x}-6sqrt{dfrac{2x}{9}}3-sqrt{dfrac{x}{2}}2,sqrt{3x}-2sqrt{12x}+dfrac{1}{3}sqrt{27x}-43, 3sqrt{2x}+5sqrt{8x}-20-sqrt{18}04,sqrt{16x+16}-sqrt{9x+9}15,sqrt{4left(1-3xright)}+sqrt{9left(1-3xright)}106,dfrac{2}{3}sqrt{x-3}+dfrac{1}{6}sqrt{x-3}-sqrt{x-3}dfrac{-2}{3}
Đọc tiếp
giải các phương trình sau:
\(1,\sqrt{18x}-6\sqrt{\dfrac{2x}{9}}=3-\sqrt{\dfrac{x}{2}}\)
\(2,\sqrt{3x}-2\sqrt{12x}+\dfrac{1}{3}\sqrt{27x}=-4\)
3, \(3\sqrt{2x}+5\sqrt{8x}-20-\sqrt{18}=0\)
\(4,\sqrt{16x+16}-\sqrt{9x+9}=1\)
\(5,\sqrt{4\left(1-3x\right)}+\sqrt{9\left(1-3x\right)}=10\)
\(6,\dfrac{2}{3}\sqrt{x-3}+\dfrac{1}{6}\sqrt{x-3}-\sqrt{x-3}=\dfrac{-2}{3}\)
2: ĐKXĐ: x>=0
\(\sqrt{3x}-2\sqrt{12x}+\dfrac{1}{3}\cdot\sqrt{27x}=-4\)
=>\(\sqrt{3x}-2\cdot2\sqrt{3x}+\dfrac{1}{3}\cdot3\sqrt{3x}=-4\)
=>\(\sqrt{3x}-4\sqrt{3x}+\sqrt{3x}=-4\)
=>\(-2\sqrt{3x}=-4\)
=>\(\sqrt{3x}=2\)
=>3x=4
=>\(x=\dfrac{4}{3}\left(nhận\right)\)
3:
ĐKXĐ: x>=0
\(3\sqrt{2x}+5\sqrt{8x}-20-\sqrt{18}=0\)
=>\(3\sqrt{2x}+5\cdot2\sqrt{2x}-20-3\sqrt{2}=0\)
=>\(13\sqrt{2x}=20+3\sqrt{2}\)
=>\(\sqrt{2x}=\dfrac{20+3\sqrt{2}}{13}\)
=>\(2x=\dfrac{418+120\sqrt{2}}{169}\)
=>\(x=\dfrac{209+60\sqrt{2}}{169}\left(nhận\right)\)
4: ĐKXĐ: x>=-1
\(\sqrt{16x+16}-\sqrt{9x+9}=1\)
=>\(4\sqrt{x+1}-3\sqrt{x+1}=1\)
=>\(\sqrt{x+1}=1\)
=>x+1=1
=>x=0(nhận)
5: ĐKXĐ: x<=1/3
\(\sqrt{4\left(1-3x\right)}+\sqrt{9\left(1-3x\right)}=10\)
=>\(2\sqrt{1-3x}+3\sqrt{1-3x}=10\)
=>\(5\sqrt{1-3x}=10\)
=>\(\sqrt{1-3x}=2\)
=>1-3x=4
=>3x=1-4=-3
=>x=-3/3=-1(nhận)
6: ĐKXĐ: x>=3
\(\dfrac{2}{3}\sqrt{x-3}+\dfrac{1}{6}\sqrt{x-3}-\sqrt{x-3}=-\dfrac{2}{3}\)
=>\(\sqrt{x-3}\cdot\left(\dfrac{2}{3}+\dfrac{1}{6}-1\right)=-\dfrac{2}{3}\)
=>\(\sqrt{x-3}\cdot\dfrac{-1}{6}=-\dfrac{2}{3}\)
=>\(\sqrt{x-3}=\dfrac{2}{3}:\dfrac{1}{6}=\dfrac{2}{3}\cdot6=\dfrac{12}{3}=4\)
=>x-3=16
=>x=19(nhận)
Đúng 1
Bình luận (0)
Cho phương trình \(\dfrac{3x^2-1}{\sqrt{2x-1}}=\sqrt{2x-1}+mx\) . tìm m để phương trình có nghiệm duy nhất
giúp mình giải bpt vs
\(\dfrac{\left|2x-1\right|-x}{2x}>1;\dfrac{2-\left|x-2\right|}{x^2-1}\ge0;\dfrac{\sqrt{x+4}-2}{4-9x^2}\le0;\dfrac{x^2-2x-3}{\sqrt[3]{3x-1}+\sqrt[3]{4-5x}}\ge0;\)\(3x^2-10x+3\ge0;\left(\sqrt{2}-x\right)\left(x^2-2\right)\left(2x-4\right)< 0;\dfrac{1}{x+9}-\dfrac{1}{x}>\dfrac{1}{2};\dfrac{2}{1-2x}\le\dfrac{3}{x+1}\)
1) nghiệm dương nhỏ nhất của phương trình \(cot\left(x-\dfrac{\pi}{6}\right)=\sqrt{3}\) là
2) phương trình \(sin\left(\dfrac{2x}{3}+\dfrac{\pi}{3}\right)=0\) có nghiệm là
3) họ nghiệm của phương trình \(cot\)(2x - 30 độ) = \(\sqrt{3}\) là
1.\(\sqrt{-4x^2+25}=x\)
2.\(\sqrt{3x^2-4x+3}=1-2x\)
3. \(\sqrt{4\left(1-x\right)^2}-\sqrt{3}=0\)
4.\(\dfrac{3\sqrt{x+5}}{\sqrt{ }x-1}< 0\)
5. \(\dfrac{3\sqrt{x-5}}{\sqrt{x+1}}\ge0\)
\(x^2-2\sqrt{3}x+1=0\) có 2 nghiệm phân biệt `x_1 ,x_2`. Tính
a) `x_1 -x_2`
b) \(\dfrac{3x^2_1+5x_1x_2+3x^2_2}{4x_1^3.x_2+4x_1.x^3_2}\)
a: \(x_1+x_2=-\dfrac{b}{a}=2\sqrt{3};x_1\cdot x_2=\dfrac{c}{a}=1\)
Đặt \(A=x_1-x_2\)
=>\(A^2=\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2\)
\(=\left(2\sqrt{3}\right)^2-4\cdot1=12-4=8\)
=>\(\left[{}\begin{matrix}x_1-x_2=2\sqrt{2}\\x_1-x_2=-2\sqrt{2}\end{matrix}\right.\)
b: \(\dfrac{3x_1^2+5x_1x_2+3x_2^2}{4x_1^3\cdot x_2+4x_1\cdot x_2^3}\)
\(=\dfrac{3\left(x_1^2+x_2^2\right)+5x_1x_2}{4x_1x_2\left(x_1^2+x_2^2\right)}\)
\(=\dfrac{3\left[\left(x_1+x_2\right)^2-2x_1x_2\right]+5x_1x_2}{4x_1x_2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]}\)
\(=\dfrac{3\left(x_1+x_2\right)^2-x_1x_2}{4x_1x_2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]}\)
\(=\dfrac{3\cdot12-1}{4\cdot1\cdot\left[12-2\cdot1\right]}=\dfrac{35}{4\cdot10}=\dfrac{7}{8}\)
Đúng 2
Bình luận (0)
1. Tìm \(m\in\left[-10;10\right]\) để pt \(\left(x^2-2x+m\right)^2-2x^2+3x-m=0\) có 4 ng pb
2. Cho biết x1,x2 là nghiệm của pt \(x^2-x+a=0\) và x3,x4 là nghiệm của pt \(x^2-4x+b=0\) . Biết rằng \(\dfrac{x2}{x1}=\dfrac{x3}{x2}=\dfrac{x4}{x3}\), b >0 . Tìm a
1.
Đặt \(x^2-2x+m=t\), phương trình trở thành \(t^2-2t+m=x\)
Ta có hệ \(\left\{{}\begin{matrix}x^2-2x+m=t\\t^2-2t+m=x\end{matrix}\right.\)
\(\Rightarrow\left(x-t\right)\left(x+t-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=t\\x=1-t\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=x^2-2x+m\\x=1-x^2+2x-m\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-x^2+3x\\m=-x^2+x+1\end{matrix}\right.\)
Phương trình hoành độ giao điểm của \(y=-x^2+x+1\) và \(y=-x^2+3x\):
\(-x^2+x+1=-x^2+3x\)
\(\Leftrightarrow x=\dfrac{1}{2}\Rightarrow y=\dfrac{5}{4}\)
Đồ thị hàm số \(y=-x^2+3x\) và \(y=-x^2+x+1\):
Dựa vào đồ thị, yêu cầu bài toán thỏa mãn khi \(m< \dfrac{5}{4}\)
Mà \(m\in\left[-10;10\right]\Rightarrow m\in[-10;\dfrac{5}{4})\)
Đúng 3
Bình luận (1)